Thanksgiving
This year we give thanks for one of the very few clues we have to the quantum nature of spacetime: black hole entropy. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, the moons of Jupiter, and space.)
Black holes are regions of spacetime where, according to the rules of Einstein’s theory of general relativity, the curvature of spacetime is so dramatic that light itself cannot escape. Physical objects (those that move at or more slowly than the speed of light) can pass through the “event horizon” that defines the boundary of the black hole, but they never escape back to the outside world. Black holes are therefore black — even light cannot escape — thus the name. At least that would be the story according to classical physics, of which general relativity is a part. Adding quantum ideas to the game changes things in important ways. But we have to be a bit vague — “adding quantum ideas to the game” rather than “considering the true quantum description of the system” — because physicists don’t yet have a fully satisfactory theory that includes both quantum mechanics and gravity.
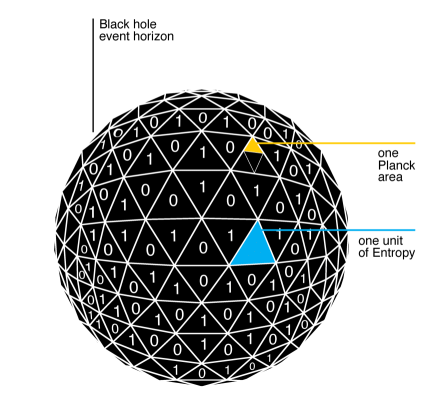
The story goes that in the early 1970’s, James Bardeen, Brandon Carter, and Stephen Hawking pointed out an analogy between the behavior of black holes and the laws of good old thermodynamics. For example, the Second Law of Thermodynamics (“Entropy never decreases in closed systems”) was analogous to Hawking’s “area theorem”: in a collection of black holes, the total area of their event horizons never decreases over time. Jacob Bekenstein, who at the time was a graduate student working under John Wheeler at Princeton, proposed to take this analogy more seriously than the original authors had in mind. He suggested that the area of a black hole’s event horizon really is its entropy, or at least proportional to it.
This annoyed Hawking, who set out to prove Bekenstein wrong. After all, if black holes have entropy then they should also have a temperature, and objects with nonzero temperatures give off blackbody radiation, but we all know that black holes are black. But he ended up actually proving Bekenstein right; black holes do have entropy, and temperature, and they even give off radiation. We now refer to the entropy of a black hole as the “Bekenstein-Hawking entropy.” (It is just a useful coincidence that the two gentlemen’s initials, “BH,” can also stand for “black hole.”)
Consider a black hole whose area of its event horizon is 
. Then its Bekenstein-Hawking entropy is
![\[S_\mathrm{BH} = \frac{c^3}{4G\hbar}A,\]](https://www.preposterousuniverse.com/blog/wp-content/ql-cache/quicklatex.com-e00278f91c29d53663b438ba10d89895_l3.png "Rendered by QuickLaTeX.com")
is the speed of light, 
is Newton’s constant of gravitation, and 
is Planck’s constant of quantum mechanics. A simple formula, but already intriguing, as it seems to combine relativity (), gravity (), and quantum mechanics () into a single expression. That’s a clue that whatever is going on here, it something to do with quantum gravity. And indeed, understanding black hole entropy and its implications has been a major focus among theoretical physicists for over four decades now, including the holographic principle, black-hole complementarity, the AdS/CFT correspondence, and the many investigations of the information-loss puzzle.
But there exists a prior puzzle: what is the black hole entropy, anyway? What physical quantity does it describe?
Entropy itself was invented as part of the development of thermodynamics is the mid-19th century, as a way to quantify the transformation of energy from a potentially useful form (like fuel, or a coiled spring) into useless heat, dissipated into the environment. It was what we might call a “phenomenological” notion, defined in terms of macroscopically observable quantities like heat and temperature, without any more fundamental basis in a microscopic theory. But more fundamental definitions came soon thereafter, once people like Maxwell and Boltzmann and Gibbs started to develop statistical mechanics, and showed that the laws of thermodynamics could be derived from more basic ideas of atoms and molecules.
Hawking’s derivation of black hole entropy was in the phenomenological vein. He showed that black holes give off radiation at a certain temperature, and then used the standard thermodynamic relations between entropy, energy, and temperature to derive his entropy formula. But this leaves us without any definite idea of what the entropy actually represents.
One of the reasons why entropy is thought of as a confusing concept is because there is more than one notion that goes under the same name. To dramatically over-simplify the situation, let’s consider three different ways of relating entropy to microscopic physics, named after three famous physicists:
- Boltzmann entropy says that we take a system with many small parts, and divide all the possible states of that system into “macrostates,” so that two “microstates” are in the same macrostate if they are macroscopically indistinguishable to us. Then the entropy is just (the logarithm of) the number of microstates in whatever macrostate the system is in.
- Gibbs entropy is a measure of our lack of knowledge. We imagine that we describe the system in terms of a probability distribution of what microscopic states it might be in. High entropy is when that distribution is very spread-out, and low entropy is when it is highly peaked around some particular state.
- von Neumann entropy is a purely quantum-mechanical notion. Given some quantum system, the von Neumann entropy measures how much entanglement there is between that system and the rest of the world.
These seem like very different things, but there are formulas that relate them to each other in the appropriate circumstances. The common feature is that we imagine a system has a lot of microscopic “degrees of freedom” (jargon for “things that can happen”), which can be in one of a large number of states, but we are describing it in some kind of macroscopic coarse-grained way, rather than knowing what its exact state actually is. The Boltzmann and Gibbs entropies worry people because they seem to be subjective, requiring either some seemingly arbitrary carving of state space into macrostates, or an explicit reference to our personal state of knowledge. The von Neumann entropy is at least an objective fact about the system. You can relate it to the others by analogizing the wave function of a system to a classical microstate. Because of entanglement, a quantum subsystem generally cannot be described by a single wave function; the von Neumann entropy measures (roughly) how many different quantum must be involved to account for its entanglement with the outside world.
So which, if any, of these is the black hole entropy? To be honest, we’re not sure. Most of us think the black hole entropy is a kind of von Neumann entropy, but the details aren’t settled.
One clue we have is that the black hole entropy is proportional to the area of the event horizon. For a while this was thought of as a big, surprising thing, since for something like a box of gas, the entropy is proportional to its total volume, not the area of its boundary. But people gradually caught on that there was never any reason to think of black holes like boxes of gas. In quantum field theory, regions of space have a nonzero von Neumann entropy even in empty space, because modes of quantum fields inside the region are entangled with those outside. The good news is that this entropy is (often, approximately) proportional to the area of the region, for the simple reason that field modes near one side of the boundary are highly entangled with modes just on the other side, and not very entangled with modes far away. So maybe the black hole entropy is just like the entanglement entropy of a region of empty space?
Would that it were so easy. Two things stand in the way. First, Bekenstein noticed another important feature of black holes: not only do they have entropy, but they have the most entropy that you can fit into a region of a fixed size (the Bekenstein bound). That’s very different from the entanglement entropy of a region of empty space in quantum field theory, where it is easy to imagine increasing the entropy by creating extra entanglement between degrees of freedom deep in the interior and those far away. So we’re back to being puzzled about why the black hole entropy is proportional to the area of the event horizon, if it’s the most entropy a region can have. That’s the kind of reasoning that leads to the holographic principle, which imagines that we can think of all the degrees of freedom inside the black hole as “really” living on the boundary, rather than being uniformly distributed inside. (There is a classical manifestation of this philosophy in the membrane paradigm for black hole astrophysics.)
The second obstacle to simply interpreting black hole entropy as entanglement entropy of quantum fields is the simple fact that it’s a finite number. While the quantum-field-theory entanglement entropy is proportional to the area of the boundary of a region, the constant of proportionality is infinity, because there are an infinite number of quantum field modes. So why isn’t the entropy of a black hole equal to infinity? Maybe we should think of the black hole entropy as measuring the amount of entanglement over and above that of the vacuum (called the Casini entropy). Maybe, but then if we remember Bekenstein’s argument that black holes have the most entropy we can attribute to a region, all that infinite amount of entropy that we are ignoring is literally inaccessible to us. It might as well not be there at all. It’s that kind of reasoning that leads some of us to bite the bullet and suggest that the number of quantum degrees of freedom in spacetime is actually a finite number, rather than the infinite number that would naively be implied by conventional non-gravitational quantum field theory.
So — mysteries remain! But it’s not as if we haven’t learned anything. The very fact that black holes have entropy of some kind implies that we can think of them as collections of microscopic degrees of freedom of some sort. (In string theory, in certain special circumstances, you can even identify what those degrees of freedom are.) That’s an enormous change from the way we would think about them in classical (non-quantum) general relativity. Black holes are supposed to be completely featureless (they “have no hair,” another idea of Bekenstein’s), with nothing going on inside them once they’ve formed and settled down. Quantum mechanics is telling us otherwise. We haven’t fully absorbed the implications, but this is surely a clue about the ultimate quantum nature of spacetime itself. Such clues are hard to come by, so for that we should be thankful.
