Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)

The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.

So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”

(Some other discussions switch the roles of heads and tails from my example.)

The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.

• “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
• “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.

The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.

Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version. …

Quantum Sleeping Beauty and the MultiverseRead More »

I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.

Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.

The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.

And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.

To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.

What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)

That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.

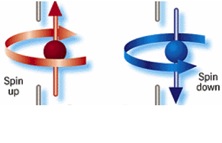The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are

“spin is up”

or

“spin is down”.

Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:

(“spin is up” + “spin is down”).

While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.

To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”

In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this: …

Why the Many-Worlds Formulation of Quantum Mechanics Is Probably CorrectRead More »

The last few years have seen a number of prominent scientists step up to microphones and belittle the value of philosophy. Stephen Hawking, Lawrence Krauss, and Neil deGrasse Tyson are well-known examples. To redress the balance a bit, philosopher of physics Wayne Myrvold has asked some physicists to explain why talking to philosophers has actually been useful to them. I was one of the respondents, and you can read my entry at the Rotman Institute blog. I was going to cross-post my response here, but instead let me try to say the same thing in different words.

Roughly speaking, physicists tend to have three different kinds of lazy critiques of philosophy: one that is totally dopey, one that is frustratingly annoying, and one that is deeply depressing.

• “Philosophy tries to understand the universe by pure thought, without collecting experimental data.”

This is the totally dopey criticism. Yes, most philosophers do not actually go out and collect data (although there are exceptions). But it makes no sense to jump right from there to the accusation that philosophy completely ignores the empirical information we have collected about the world. When science (or common-sense observation) reveals something interesting and important about the world, philosophers obviously take it into account. (Aside: of course there are bad philosophers, who do all sorts of stupid things, just as there are bad practitioners of every field. Let’s concentrate on the good ones, of whom there are plenty.)

Philosophers do, indeed, tend to think a lot. This is not a bad thing. All of scientific practice involves some degree of “pure thought.” Philosophers are, by their nature, more interested in foundational questions where the latest wrinkle in the data is of less importance than it would be to a model-building phenomenologist. But at its best, the practice of philosophy of physics is continuous with the practice of physics itself. Many of the best philosophers of physics were trained as physicists, and eventually realized that the problems they cared most about weren’t valued in physics departments, so they switched to philosophy. But those problems — the basic nature of the ultimate architecture of reality at its deepest levels — are just physics problems, really. And some amount of rigorous thought is necessary to make any progress on them. Shutting up and calculating isn’t good enough.

• “Philosophy is completely useless to the everyday job of a working physicist.”

Now we have the frustratingly annoying critique. Because: duh. If your criterion for “being interesting or important” comes down to “is useful to me in my work,” you’re going to be leading a fairly intellectually impoverished existence. Nobody denies that the vast majority of physics gets by perfectly well without any input from philosophy at all. (“We need to calculate this loop integral! Quick, get me a philosopher!”) But it also gets by without input from biology, and history, and literature. Philosophy is interesting because of its intrinsic interest, not because it’s a handmaiden to physics. I think that philosophers themselves sometimes get too defensive about this, trying to come up with reasons why philosophy is useful to physics. Who cares?

Nevertheless, there are some physics questions where philosophical input actually is useful. Foundational questions, such as the quantum measurement problem, the arrow of time, the nature of probability, and so on. Again, a huge majority of working physicists don’t ever worry about these problems. But some of us do! And frankly, if more physicists who wrote in these areas would make the effort to talk to philosophers, they would save themselves from making a lot of simple mistakes.

• “Philosophers care too much about deep-sounding meta-questions, instead of sticking to what can be observed and calculated.”

Finally, the deeply depressing critique. Here we see the unfortunate consequence of a lifetime spent in an academic/educational system that is focused on taking ambitious dreams and crushing them into easily-quantified units of productive work. The idea is apparently that developing a new technique for calculating a certain wave function is an honorable enterprise worthy of support, while trying to understand what wave functions actually are and how they capture reality is a boring waste of time. I suspect that a substantial majority of physicists who use quantum mechanics in their everyday work are uninterested in or downright hostile to attempts to understand the quantum measurement problem.

This makes me sad. I don’t know about all those other folks, but personally I did not fall in love with science as a kid because I was swept up in the romance of finding slightly more efficient calculational techniques. Don’t get me wrong — finding more efficient calculational techniques is crucially important, and I cheerfully do it myself when I think I might have something to contribute. But it’s not the point — it’s a step along the way to the point.

The point, I take it, is to understand how nature works. Part of that is knowing how to do calculations, but another part is asking deep questions about what it all means. That’s what got me interested in science, anyway. And part of that task is understanding the foundational aspects of our physical picture of the world, digging deeply into issues that go well beyond merely being able to calculate things. It’s a shame that so many physicists don’t see how good philosophy of science can contribute to this quest. The universe is much bigger than we are and stranger than we tend to imagine, and I for one welcome all the help we can get in trying to figure it out.