Entropy increases. Closed systems become increasingly disordered over time. So says the Second Law of Thermodynamics, one of my favorite notions in all of physics.
At least, entropy usually increases. If we define entropy by first defining “macrostates” — collections of individual states of the system that are macroscopically indistinguishable from each other — and then taking the logarithm of the number of microstates per macrostate, as portrayed in this blog’s header image, then we don’t expect entropy to always increase. According to Boltzmann, the increase of entropy is just really, really probable, since higher-entropy macrostates are much, much bigger than lower-entropy ones. But if we wait long enough — really long, much longer than the age of the universe — a macroscopic system will spontaneously fluctuate into a lower-entropy state. Cream and coffee will unmix, eggs will unbreak, maybe whole universes will come into being. But because the timescales are so long, this is just a matter of intellectual curiosity, not experimental science.
That’s what I was taught, anyway. But since I left grad school, physicists (and chemists, and biologists) have become increasingly interested in ultra-tiny systems, with only a few moving parts. Nanomachines, or the molecular components inside living cells. In systems like that, the occasional downward fluctuation in entropy is not only possible, it’s going to happen relatively frequently — with crucial consequences for how the real world works.
Accordingly, the last fifteen years or so has seen something of a revolution in non-equilibrium statistical mechanics — the study of statistical systems far from their happy resting states. Two of the most important results are the Crooks Fluctuation Theorem (by Gavin Crooks), which relates the probability of a process forward in time to the probability of its time-reverse, and the Jarzynski Equality (by Christopher Jarzynski), which relates the change in free energy between two states to the average amount of work done on a journey between them. (Professional statistical mechanics are so used to dealing with inequalities that when they finally do have an honest equation, they call it an “equality.”) There is a sense in which these relations underlie the good old Second Law; the Jarzynski equality can be derived from the Crooks Fluctuation Theorem, and the Second Law can be derived from the Jarzynski Equality. (Though the three relations were discovered in reverse chronological order from how they are used to derive each other.)
Still, there is a mystery lurking in how we think about entropy and the Second Law — a puzzle that, like many such puzzles, I never really thought about until we came up with a solution. Boltzmann’s definition of entropy (logarithm of number of microstates in a macrostate) is very conceptually clear, and good enough to be engraved on his tombstone. But it’s not the only definition of entropy, and it’s not even the one that people use most often.
Rather than referring to macrostates, we can think of entropy as characterizing something more subjective: our knowledge of the state of the system. That is, we might not know the exact position x and momentum p of every atom that makes up a fluid, but we might have some probability distribution ρ(x,p) that tells us the likelihood the system is in any particular state (to the best of our knowledge). Then the entropy associated with that distribution is given by a different, though equally famous, formula:
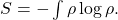
That is, we take the probability distribution ρ, multiply it by its own logarithm, and integrate the result over all the possible states of the system, to get (minus) the entropy. A formula like this was introduced by Boltzmann himself, but these days is often associated with Josiah Willard Gibbs, unless you are into information theory, where it’s credited to Claude Shannon. Don’t worry if the symbols are totally opaque; the point is that low entropy means we know a lot about the specific state a system is in, and high entropy means we don’t know much at all.
In appropriate circumstances, the Boltzmann and Gibbs formulations of entropy and the Second Law are closely related to each other. But there’s a crucial difference: in a perfectly isolated system, the Boltzmann entropy tends to increase, but the Gibbs entropy stays exactly constant. In an open system — allowed to interact with the environment — the Gibbs entropy will go up, but it will only go up. It will never fluctuate down. (Entropy can decrease through heat loss, if you put your system in a refrigerator or something, but you know what I mean.) The Gibbs entropy is about our knowledge of the system, and as the system is randomly buffeted by its environment we know less and less about its specific state. So what, from the Gibbs point of view, can we possibly mean by “entropy rarely, but occasionally, will fluctuate downward”?
I won’t hold you in suspense. Since the Gibbs/Shannon entropy is a feature of our knowledge of the system, the way it can fluctuate downward is for us to look at the system and notice that it is in a relatively unlikely state — thereby gaining knowledge.
But this operation of “looking at the system” doesn’t have a ready implementation in how we usually formulate statistical mechanics. Until now! My collaborators Tony Bartolotta, Stefan Leichenauer, Jason Pollack, and I have written a paper formulating statistical mechanics with explicit knowledge updating via measurement outcomes. (Some extra figures, animations, and codes are available at this web page.)
The Bayesian Second Law of Thermodynamics
Anthony Bartolotta, Sean M. Carroll, Stefan Leichenauer, and Jason Pollack
We derive a generalization of the Second Law of Thermodynamics that uses Bayesian updates to explicitly incorporate the effects of a measurement of a system at some point in its evolution. By allowing an experimenter’s knowledge to be updated by the measurement process, this formulation resolves a tension between the fact that the entropy of a statistical system can sometimes fluctuate downward and the information-theoretic idea that knowledge of a stochastically-evolving system degrades over time. The Bayesian Second Law can be written as ΔH(ρm,ρ)+⟨Q⟩F|m≥0, where ΔH(ρm,ρ) is the change in the cross entropy between the original phase-space probability distribution ρ and the measurement-updated distribution ρm, and ⟨Q⟩F|m is the expectation value of a generalized heat flow out of the system. We also derive refined versions of the Second Law that bound the entropy increase from below by a non-negative number, as well as Bayesian versions of the Jarzynski equality. We demonstrate the formalism using simple analytical and numerical examples.
The crucial word “Bayesian” here refers to Bayes’s Theorem, a central result in probability theory. …
The Bayesian Second Law of ThermodynamicsRead More »

 One of the things Kip talks about is that the film refers to the concept of a tesseract, which he thought was fun. A tesseract is a four-dimensional version of a cube; you can’t draw it faithfully in two dimensions, but with a little imagination you can get the idea from the picture on the right. Kip mentions that he first heard of the concept of a tesseract in George Gamow’s classic book
One of the things Kip talks about is that the film refers to the concept of a tesseract, which he thought was fun. A tesseract is a four-dimensional version of a cube; you can’t draw it faithfully in two dimensions, but with a little imagination you can get the idea from the picture on the right. Kip mentions that he first heard of the concept of a tesseract in George Gamow’s classic book