Science – Page 15 – Sean Carroll

Guest Post: Lance Dixon on Calculating Amplitudes

October 3, 2013 / 19 Comments

This year’s Sakurai Prize of the American Physical Society, one of the most prestigious awards in theoretical particle physics, has been awarded to Zvi Bern, Lance Dixon, and David Kosower “for pathbreaking contributions to the calculation of perturbative scattering amplitudes, which led to a deeper understanding of quantum field theory and to powerful new tools for computing QCD processes.” An “amplitude” is the fundamental thing one wants to calculate in quantum mechanics — the probability that something happens (like two particles scattering) is given by the amplitude squared. This is one of those topics that is absolutely central to how modern particle physics is done, but it’s harder to explain the importance of a new set of calculational techniques than something marketing-friendly like finding a new particle. Nevertheless, the field pioneered by Bern, Dixon, and Kosower made a splash in the news recently, with Natalie Wolchover’s masterful piece in Quanta about the “Amplituhedron” idea being pursued by Nima Arkani-Hamed and collaborators. (See also this recent piece in Scientific American, if you subscribe.)

I thought about writing up something about scattering amplitudes in gauge theories, similar in spirit to the post on effective field theory, but quickly realized that I wasn’t nearly familiar enough with the details to do a decent job. And you’re lucky I realized it, because instead I asked Lance Dixon if he would contribute a guest post. Here’s the result, which sets a new bar for guest posts in the physics blogosphere. Thanks to Lance for doing such a great job.

—————————————————————-

“Amplitudes: The untold story of loops and legs”

Sean has graciously offered me a chance to write something about my research on scattering amplitudes in gauge theory and gravity, with my longtime collaborators, Zvi Bern and David Kosower, which has just been recognized by the Sakurai Prize for theoretical particle physics.

In short, our work was about computing things that could in principle be computed with Feynman diagrams, but it was much more efficient to use some general principles, instead of Feynman diagrams. In one sense, the collection of ideas might be considered “just tricks”, because the general principles have been around for a long time. On the other hand, they have provided results that have in turn led to new insights about the structure of gauge theory and gravity. They have also produced results for physics processes at the Large Hadron Collider that have been unachievable by other means.

The great Russian physicist, Lev Landau, a contemporary of Richard Feynman, has a quote that has been a continual source of inspiration for me: “A method is more important than a discovery, since the right method will lead to new and even more important discoveries.”

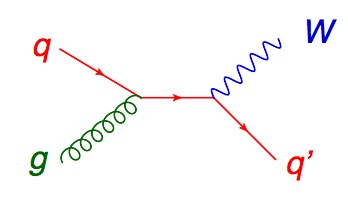
The work with Zvi and David, which has spanned two decades, is all about scattering amplitudes, which are the complex numbers that get squared in quantum mechanics to provide probabilities for incoming particles to scatter into outgoing ones. High energy physics is essentially the study of scattering amplitudes, especially those for particles moving very close to the speed of light. Two incoming particles at a high energy collider smash into each other, and a multitude of new, outgoing particles can be created from their relativistic energy. In perturbation theory, scattering amplitudes can be computed (in principle) by drawing all Feynman diagrams. The first order in perturbation theory is called tree level, because you draw all diagrams without any closed loops, which look roughly like trees. For example, one of the two tree-level Feynman diagrams for a quark and a gluon to scatter into a W boson (carrier of the weak force) and a quark is shown here.

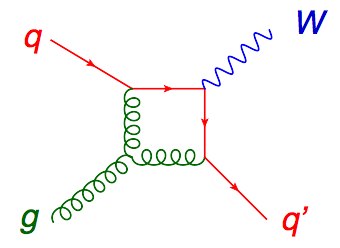
We write this process as qg → Wq. To get the next approximation (called NLO) you do the one loop corrections, all diagrams with one closed loop. One of the 11 diagrams for the same process is shown here.

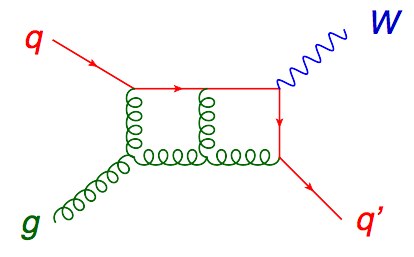
Then two loops (one diagram out of hundreds is shown here), and so on.

The forces underlying the Standard Model of particle physics are all described by gauge theories, also called Yang-Mills theories. The one that holds the quarks and gluons together inside the proton is a theory of “color” forces called quantum chromodynamics (QCD). The physics at the discovery machines called hadron colliders — the Tevatron and the LHC — is dominantly that of QCD. Feynman rules, which assign a formula to each Feynman diagram, have been known since Feynman’s work in the 1940s. The ones for QCD have been known since the 1960s. Still, computing scattering amplitudes in QCD has remained a formidable problem for theorists.

Back around 1990, the state of the art for scattering amplitudes in QCD was just one loop. It was also basically limited to “four-leg” processes, which means two particles in and two particles out. For example, gg → gg (two gluons in, two gluons out). This process (or reaction) gives two “jets” of high energy hadrons at the Tevatron or the LHC. It has a very high rate (probability of happening), and gives our most direct probe of the behavior of particles at very short distances.

Another reaction that was just being computed at one loop around 1990 was qg → Wq (one of whose Feynman diagrams you saw earlier). This is another copious process and therefore an important background at the LHC. But these two processes are just the tip of an enormous iceberg; experimentalists can easily find LHC events with six or more jets (http://arxiv.org/abs/arXiv:1107.2092, http://arxiv.org/abs/arXiv:1110.3226, http://arxiv.org/abs/arXiv:1304.7098), each one coming from a high energy quark or gluon. There are many other types of complex events that they worry about too.

A big problem for theorists is that the number of Feynman diagrams grows rapidly with both the number of loops, and with the number of legs. In the case of the number of legs, for example, there are only 11 Feynman diagrams for qg → Wq. One diagram a day, and you are done in under two weeks; no problem. However, if you want to do instead the series of processes: qg → Wqg, qg → Wqgg, qg → Wqggg, qg → Wqgggg, you face 110, 1253, 16,648 and 256,265 Feynman diagrams. That could ruin your whole decade (or more). [See the figure; the ring-shaped blobs stand for the sum of all one-loop Feynman diagrams.]

It’s not just the raw number of diagrams. Many of the diagrams with large numbers of external particles are much, much messier than the 11 diagrams for qg → Wq. Plus the messy diagrams tend to be numerically unstable, causing problems when you try to get numbers out. This problem definitely calls out for a new method.

Why care about all these scattering amplitudes at all? …

Guest Post: Lance Dixon on Calculating AmplitudesRead More »

Guest Post: Lance Dixon on Calculating Amplitudes Read More »

19 Comments

Dark Energy Detectives

September 16, 2013 / 12 Comments

We start the night’s work early with an inter-continental tele-conference before dinner. After dinner, we prepare the software and telescope until sunset, when the hunt begins. Working through the night (and through a few pots of coffee and bags of cookies), we emerge a few hundred images closer to understanding dark energy and its effects on the celestial objects deep in the night sky. Just after sunrise, we hit the hay, but our minds often keep crunching numbers or sifting puzzles that arose during our observations, as the work from our night bleeds into our dreamscape.

The Dark Energy Survey recently embarked on a five-year mission to better understand the universe. It’s not a starship, though, it’s an international collaboration using the Blanco telescope in Chile to study the effects of dark energy on the evolution of the universe through a variety of probes — supernovae, baryon acoustic oscillations, weak gravitational lensing, and counts of galaxy clusters.

Dark Energy Detectives is a blog that accompanies the project, and it’s well worth reading to get a sense for what it’s like to do modern astronomy. (Hat tip Nick Suntzeff.) The entries are engaging and well-written, mostly by Brian Nord from Fermilab. We’ve progressed quite a bit since Galileo’s time; we no longer peer through the eyepiece and sketch what we see. Actually there’s not much peering through eyepieces at all, it’s all done by electronics. But you still need to stay up through the night and coax the telescope through it’s targets. And I’m sure Galileo enjoyed more than a few cups of espresso and bags of biscotti along the way.

Dark Energy Detectives Read More »

12 Comments

Atoms With Consciousness, Matter With Curiosity

September 4, 2013 / 34 Comments

Probably I’m the last scientfically-oriented person in the world to discover this, but Richard Feynman wrote a poem that he read as part of an address to the National Academy of Sciences. I stumbled across it because I was actually looking for scientists who were familiar with work of the poet Muriel Rukeyser — anyone have any suggestions? Anyway, here’s Feynman:

There are the rushing waves
mountains of molecules
each stupidly minding its own business
trillions apart
yet forming white surf in unison

Ages on ages
before any eyes could see
year after year
thunderously pounding the shore as now.
For whom, for what?
On a dead planet
with no life to entertain.

Never at rest
tortured by energy
wasted prodigiously by the Sun
poured into space.
A mite makes the sea roar.

Deep in the sea
all molecules repeat
the patterns of one another
till complex new ones are formed.
They make others like themselves
and a new dance starts.
Growing in size and complexity
living things
masses of atoms
DNA, protein
dancing a pattern ever more intricate.

Out of the cradle
onto dry land
here it is
standing:
atoms with consciousness;
matter with curiosity.

Stands at the sea,
wonders at wondering: I
a universe of atoms
an atom in the Universe.

Nobody is surprised, of course, that Feynman was a card-carrying dysteleological physicalist. More interesting is that he chose to highlight this kind of question — the emergence of complexity and consciousness from the blind play of atoms, stupidly minding their own business — rather than something about particle physics, for example. As much as reductionists get a bad name in some circles, the good ones do appreciate the bigger picture.

Atoms With Consciousness, Matter With Curiosity Read More »

34 Comments

The Higgs Boson vs. Boltzmann Brains

August 22, 2013 / 76 Comments

Kim Boddy and I have just written a new paper, with maybe my favorite title ever.

Can the Higgs Boson Save Us From the Menace of the Boltzmann Brains?
Kimberly K. Boddy, Sean M. Carroll
(Submitted on 21 Aug 2013)

The standard ΛCDM model provides an excellent fit to current cosmological observations but suffers from a potentially serious Boltzmann Brain problem. If the universe enters a de Sitter vacuum phase that is truly eternal, there will be a finite temperature in empty space and corresponding thermal fluctuations. Among these fluctuations will be intelligent observers, as well as configurations that reproduce any local region of the current universe to arbitrary precision. We discuss the possibility that the escape from this unacceptable situation may be found in known physics: vacuum instability induced by the Higgs field. Avoiding Boltzmann Brains in a measure-independent way requires a decay timescale of order the current age of the universe, which can be achieved if the top quark pole mass is approximately 178 GeV. Otherwise we must invoke new physics or a particular cosmological measure before we can consider ΛCDM to be an empirical success.

We apply some far-out-sounding ideas to very down-to-Earth physics. Among other things, we’re suggesting that the mass of the top quark might be heavier than most people think, and that our universe will decay in another ten billion years or so. Here’s a somewhat long-winded explanation.

A room full of monkeys, hitting keys randomly on a typewriter, will eventually bang out a perfect copy of Hamlet. Assuming, of course, that their typing is perfectly random, and that it keeps up for a long time. An extremely long time indeed, much longer than the current age of the universe. So this is an amusing thought experiment, not a viable proposal for creating new works of literature (or old ones).

There’s an interesting feature of what these thought-experiment monkeys end up producing. Let’s say you find a monkey who has just typed Act I of Hamlet with perfect fidelity. You might think “aha, here’s when it happens,” and expect Act II to come next. But by the conditions of the experiment, the next thing the monkey types should be perfectly random (by which we mean, chosen from a uniform distribution among all allowed typographical characters), and therefore independent of what has come before. The chances that you will actually get Act II next, just because you got Act I, are extraordinarily tiny. For every one time that your monkeys type Hamlet correctly, they will type it incorrectly an enormous number of times — small errors, large errors, all of the words but in random order, the entire text backwards, some scenes but not others, all of the lines but with different characters assigned to them, and so forth. Given that any one passage matches the original text, it is still overwhelmingly likely that the passages before and after are random nonsense.

That’s the Boltzmann Brain problem in a nutshell. Replace your typing monkeys with a box of atoms at some temperature, and let the atoms randomly bump into each other for an indefinite period of time. Almost all the time they will be in a disordered, high-entropy, equilibrium state. Eventually, just by chance, they will take the form of a smiley face, or Michelangelo’s David, or absolutely any configuration that is compatible with what’s inside the box. If you wait long enough, and your box is sufficiently large, you will get a person, a planet, a galaxy, the whole universe as we now know it. But given that some of the atoms fall into a familiar-looking arrangement, we still expect the rest of the atoms to be completely random. Just because you find a copy of the Mona Lisa, in other words, doesn’t mean that it was actually painted by Leonardo or anyone else; with overwhelming probability it simply coalesced gradually out of random motions. Just because you see what looks like a photograph, there’s no reason to believe it was preceded by an actual event that the photo purports to represent. If the random motions of the atoms create a person with firm memories of the past, all of those memories are overwhelmingly likely to be false.

This thought experiment was originally relevant because Boltzmann himself (and before him Lucretius, Hume, etc.) suggested that our world might be exactly this: a big box of gas, evolving for all eternity, out of which our current low-entropy state emerged as a random fluctuation. As was pointed out by Eddington, Feynman, and others, this idea doesn’t work, for the reasons just stated; given any one bit of universe that you might want to make (a person, a solar system, a galaxy, and exact duplicate of your current self), the rest of the world should still be in a maximum-entropy state, and it clearly is not. This is called the “Boltzmann Brain problem,” because one way of thinking about it is that the vast majority of intelligent observers in the universe should be disembodied brains that have randomly fluctuated out of the surrounding chaos, rather than evolving conventionally from a low-entropy past. That’s not really the point, though; the real problem is that such a fluctuation scenario is cognitively unstable — you can’t simultaneously believe it’s true, and have good reason for believing its true, because it predicts that all the “reasons” you think are so good have just randomly fluctuated into your head!

All of which would seemingly be little more than fodder for scholars of intellectual history, now that we know the universe is not an eternal box of gas. The observable universe, anyway, started a mere 13.8 billion years ago, in a very low-entropy Big Bang. That sounds like a long time, but the time required for random fluctuations to make anything interesting is enormously larger than that. (To make something highly ordered out of something with entropy S, you have to wait for a time of order e^S. Since macroscopic objects have more than 10²³ particles, S is at least that large. So we’re talking very long times indeed, so long that it doesn’t matter whether you’re measuring in microseconds or billions of years.) Besides, the universe is not a box of gas; it’s expanding and emptying out, right?

Ah, but things are a bit more complicated than that. We now know that the universe is not only expanding, but also accelerating. The simplest explanation for that — not the only one, of course — is that empty space is suffused with a fixed amount of vacuum energy, a.k.a. the cosmological constant. Vacuum energy doesn’t dilute away as the universe expands; there’s nothing in principle from stopping it from lasting forever. So even if the universe is finite in age now, there’s nothing to stop it from lasting indefinitely into the future.

But, you’re thinking, doesn’t the universe get emptier and emptier as it expands, leaving no particles to fluctuate? Only up to a point. A universe with vacuum energy accelerates forever, and as a result we are surrounded by a cosmological horizon — objects that are sufficiently far away can never get to us or even send signals, as the space in between expands too quickly. And, as Stephen Hawking and Gary Gibbons pointed out in the 1970’s, such a cosmology is similar to a black hole: there will be radiation associated with that horizon, with a constant temperature.

In other words, a universe with a cosmological constant is like a box of gas (the size of the horizon) which lasts forever with a fixed temperature. Which means there are random fluctuations. If we wait long enough, some region of the universe will fluctuate into absolutely any configuration of matter compatible with the local laws of physics. Atoms, viruses, people, dragons, what have you. The room you are in right now (or the atmosphere, if you’re outside) will be reconstructed, down to the slightest detail, an infinite number of times in the future. In the overwhelming majority of times that your local environment does get created, the rest of the universe will look like a high-entropy equilibrium state (in this case, empty space with a tiny temperature). All of those copies of you will think they have reliable memories of the past and an accurate picture of what the external world looks like — but they would be wrong. And you could be one of them.

That would be bad. …

The Higgs Boson vs. Boltzmann BrainsRead More »

The Higgs Boson vs. Boltzmann Brains Read More »

76 Comments

A Map of the Research Literature

August 17, 2013 / 12 Comments

The arxiv, started by Paul Ginsparg in 1991, was a pioneer for the Open Access movement in scientific publishing. Most (many?) working physicists, and an increasing number of scientists in other fields, take it for granted that they will share their research articles freely with everyone in the world by submitting to arxiv. The current submission rate is about 8,000 papers per month, and still growing linearly or possibly a bit faster.

In addition to providing fast and easy communication of new papers, the arxiv is a resource ripe for data-mining. Say hello to Paperscape, a project by Damien George of Cambridge and Rob Knegjens at Nikhef in the Netherlands. This fun (and possibly useful) new tool creates a categorized/zoomable/clickable/searchable map of every paper on the arxiv. Apparently it’s been around since March, but I only heard about it yesterday, possibly because of this post on physicsworld.com. So here’s the birds-eye view of what the arxiv looks like:

There is a lot of data displayed here in quite a dense way. The different colors represent different arxiv categories: condensed matter, astrophysics, and so on. High-energy physics dominates the map, in part because that was the first field to participate in arxiv in the first place. Each circle is an individual paper, with the size representing the number of times that paper has been cited (within arxiv). You can pick out some of the big hits in the field — the accelerating universe, cosmic microwave background observations, AdS/CFT, extra dimensions, and so on. The locations aren’t random, either; circles are placed in proximity depending on how often they cite each other. So the fact that contiguous regions all have the same color isn’t built into the mapping algorithm, it’s a consequence of the (perfectly predictable) fact that papers in the same field cite each other more than papers in other fields.

As you zoom in, the papers become more legible — when a circle becomes big enough, a word or phrase from the title appears, and eventually the author’s name. Here’s one of my papers, a bit standoffish from its surroundings:

You can also search for authors, title words, and so on. Of course the first thing any working physicist will do will search for themselves. Here I am, my life’s work reduced to handy graphical form:

Click for a bigger and more legible version — or just go search yourself, by typing “?a s.m.carroll” into the search box. (Much more fun that way.) The white circles are the search results. Scattered all over the place, to nobody’s surprise; but most of my papers (and definitely the ones with the biggest circles) lie in that mixed-color overlap between gravity/quantum cosmology, astrophysics, high energy formal theory, and high-energy phenomenology. Somewhat zoomed-in:

Very fun in a narcissistic sort of way, but once you’re done ego-surfing I imagine it will also be a useful tool. Hopefully most researchers are already aware of the important papers in their areas of interest, but maybe you can discover some apparently highly-cited work right next to yours that you hadn’t known about. Or, even better, some less-cited work that maybe deserves more attention. Certainly it could be useful to people trying to dive into fields in which they are not yet experts. There are also options to look for recent papers, trending work, and more. Of course there is a blog.

Congratulations to Damien George and Rob Knegjens for such an interesting project. I wonder if they will write a paper about it and post it to arxiv?

A Map of the Research Literature Read More »

12 Comments

Let’s Stop Using the Word “Scientism”

August 14, 2013 / 57 Comments

Steven Pinker has kicked up a cloud of dust with a seemingly mild claim, addressed to people in the humanities: Science Is Not Your Enemy. And he’s right, it’s not! Science is merely an extremely effective method for gaining empirical knowledge of the world, and empirical knowledge of the world should not strike fear into any self-respecting intellectual person. Or if it does, perhaps you should contemplate a different form of employment, like U.S. Senator.

The devil is in the details, of course, and plenty of people have objected to the specific ways in which Pinker has argued that science is your friend, and others have defended him. Here are takes by Jerry Coyne, Eric MacDonald, and Massimo Pigliucci. I don’t mean to add anything deep or comprehensive to the debate, but I do want to make a suggestion that, if adopted, would make the world a better place: the word “scientism” should be dropped from the vocabulary of this discussion.

Now (like Pinker), I am a descriptivist rather than a prescriptivist when it comes to language. Word usage is not “right” or “wrong,” it’s just “useful” or “unhelpful.” So the point here is that use of the word “scientism” is unhelpful, not that people are using the “wrong” definition. It’s unhelpful because it’s ill-defined, and acts as a license for lazy thinking. (It wasn’t too long ago that I acknowledged the potential usefulness of the term, but now I see the error of my ways.)

The working definition of “scientism” is “the belief that science is the right approach to use in situations where science actually isn’t the right approach at all.” Nobody actually quotes this definition, but it accurately matches how the word is used. The problem should be obvious — the areas in which science is the right approach are not universally agreed upon. So instead of having an interesting substantive discussion about a real question (“For what kinds of problems is a scientific approach the best one?”) we instead have a dopey and boring definitional one (“What does the word `scientism’ mean?”).

I don’t know of anyone in the world who thinks that science is the right tool to use for every problem. Pinker joins Alex Rosenberg, who has tried to rehabilitate the word “scientism,” claiming it as a badge of honor, and using it to mean a view that “the methods of science are the only reliable ways to secure knowledge of anything.” But even Alex firmly rejects the idea that science can be used to discover objective moral truths — and others think it can, a view which is sometimes labeled as “scientism.” You can see the confusion.

Someone might respond, “but `scientism’ is a useful shorthand for a set of views that many people seem to hold.” No, it’s not. Here are some possible views that might be described as “scientism”:

Science is the source of all interesting, reliable facts about the world.
Philosophy and morality and aesthetics should be subsumed under the rubric of science.
Science can provide an objective grounding for judgments previously thought to be subjective.
Humanities and the arts would be improved by taking a more scientific approach.
The progress of science is an unalloyed good for the world.
All forms of rational thinking are essentially science.
Eventually we will understand all the important questions of human life on a scientific basis.
Reductionism is the best basis for complete understanding of complicated systems.
There is no supernatural realm, only the natural world that science can investigate.

The problem is that, when you use the word “scientism,” you (presumably) know exactly what you are talking about. You mean to include some of the above supposed sins, but not necessarily all of them. But if you aren’t completely explicit about what you mean every time you use the term, people will misunderstand you.

Indeed, you might even misunderstand yourself. By which I mean, using vague words like this is an invitation to lazy thinking. Rather than arguing against the specific points someone else makes, you wrap them all up in a catch-all term of disapprobation, and then argue against that. Saves time, but makes for less precise and productive discussion.

Given that the only productive way to use a word like “scientism” — something vaguely sinister, ill-defined, used primarily as an accusation against people who would not describe themselves that way — would be to provide an explicit and careful definition every time the word is invoked, why use it at all? I’m not saying you can’t disagree with specific claims made by Pinker or anyone else. If you think people are making some particular mistake, that’s fine — just say what the mistake is.

I take the main point of Pinker’s piece to be the same as Feynman’s discussion of the beauty of a flower, or Dawkins’s Unweaving the Rainbow — science is not opposed to the humanities or the arts, but enhances them by giving us a deeper understanding. With that, I couldn’t agree more. We can disagree with some of the specific contentions in a constructive way, but lumping everything we don’t like into one catch-all word isn’t useful.

TL;DR: The word “scientism” doesn’t helpfully delineate a coherent position, it unhelpfully flattens important distinctions and creates a false target. We can do better.

Let’s Stop Using the Word “Scientism” Read More »

57 Comments

Quantum Mechanics Explained

August 13, 2013 / 23 Comments

Yesterday was Erwin Schrödinger’s birthday, as those of you who actually visit the Google home page would have noticed.

This auspicious event nudged me (a day late, admittedly) to do something I’ve been contemplating for a while now — explain the basic ideas of quantum mechanics the best way I know how, at an accessible level (no equations) but without any frustrating length limitations. Sure, you can do pretty well in just five words, but sometimes you need to be a little more expansive.

Fortunately, very little work was required, since I’ve already done it! This is what happens when you write popular books on physics. Depending on the subject, one of the early chapters is guaranteed to be an overview of either quantum mechanics or general relativity. When I wrote From Eternity to Here, I fooled everybody with an unprecedented step: I put my intro to QM late in the book, in Chapter 11. (The intro to GR was, admittedly, Chapter 5.)

I tried hard in that chapter to do justice to the important ideas of quantum mechanics — superpositions, entanglement, measurement, decoherence, probabilities — without getting bogged down in technical details. I glossed over the fact that amplitudes are complex numbers, although I certainly emphasized that they can be negative as well as positive. It laid some groundwork for the rest of the book, but that chapter itself didn’t really talk about (or rely on previous discussion of) entropy, cosmology, or the arrow of time.

So I’ve simply made it into its own web page, here freely available to all:

Quantum Mechanics Made Easy

It’s about 13,000 words — there’s a lot to explain. But now I have somewhere to point to if someone wants to know the basics.

Of course, physicists famously don’t quite agree about what quantum mechanics actually says. Naturally, I’m giving the version I think is right. At the end I try to distinguish what everyone agrees on from what is still conjectural, but this is certainly not the place to go for an overview of all the different interpretations. It’s just the particular view of one cheerful psi-ontologist.

Quantum Mechanics Explained Read More »

23 Comments

Philosophy, Physics, and How It All Fits Together

August 3, 2013 / 43 Comments

Richard Marshall at 3AM magazine has been doing a series of interviews with all kinds of thinkers, especially philosophers; some recent examples include Dan Dennett, Tim Maudlin, Rebecca Kukla, Alex Rosenberg, and Craig Callender. And I’m the latest subject. Given the venue, we talk as much (or more) about philosophy than about physics, and a lot about how they fit together.

Spoiler alert: I think it’s possible to have productive grown-up interactions between philosophy and science. I guess I’m just a radical bomb-thrower at heart.

Click through if this kind of thing floats your boat:

I think emergence is absolutely central to how naturalists should think about the world, and how we should find room for higher-level concepts from tables to free will in a way compatible with the scientific image. But “weak” emergence, not strong emergence. That is simply the idea that there are multiple theories/languages/vocabularies/ontologies that we can use to usefully describe the world, each appropriate at different levels of coarse-graining and precision. I always return to the example of thermodynamics (fluids, energy, pressure, entropy) and kinetic theory (collections of atoms and molecules with individual positions and momenta). Here we have two ways of talking, each perfectly valid within a domain of applicability, but with the domain of one theory (thermodynamics) living strictly inside the domain of the other (kinetic theory). Crucially, the “emergent” higher-level theory can exhibit features that you might naively think are ruled out by the lower-level rules; in particular, thermodynamics famously has an arrow of time defined by the Second Law (entropy increases in isolated systems), whereas the microscopic rules of the lower-level theory are completely time-symmetric and arrowless.

I think this example serves as a paradigm for how we can connect the manifest image to the scientific image. Sure, there’s nothing like “free will” anywhere to be found in the ultimate laws of physics. But that’s not the only question to ask; at the higher-level description, we should ask whether our best emergent theory of human beings includes the idea that they are (in the right circumstances) rational decision-making agents with freedom of action. Until we come up with a better description of human beings, I’m perfectly happy to say that free will is “real.” It’s not to be found in the most fundamental ontology, but it’s not incompatible with it either; it’s simply a crucial part of our best higher-level vocabulary.

Philosophy, Physics, and How It All Fits Together Read More »

43 Comments

Talking Back to Your Elders

July 29, 2013 / 59 Comments

When I was young and as yet unformed as a theoretical physicist, cosmology was in a transitional period. We had certainly moved beyond the relatively barren landscape of the 60’s and 70’s, when pretty much the only things one had to hang one’s hat on were very basic features like expansion, rough homogeneity, and the (existence of) the cosmic microwave background. By the late 80’s we were beginning to see the first surveys of large-scale structure, there was good evidence for dark matter, and the inflationary paradigm was somewhat developed. In the 90’s things changed quite rapidly, unbelievably so in retrospect. We detected primordial anisotropies in the CMB and began to study them in detail, large-scale-structure surveys really took off, we discovered the acceleration of the universe, and techniques like gravitational lensing matured into usefulness.

My students and postdocs will readily testify that I am fond of complaining how much harder it is to come up with interesting new ideas that aren’t already ruled out by the data.

In an interesting and provocative post, Peter Coles bemoans a generational shift among cosmologists: “When I was a lad the students and postdocs were a lot more vocal at meetings than they are now.” In particular, Peter is worried that people in the field (young and old) are “willing to believe too much,” and correspondingly unwilling to propose dramatic new ideas that might run counter to received opinion. Or even, presumably, just to express doubt that received opinion is on the right track. After all, even with all we’ve learned, there’s certainly much we don’t yet know.

I’m not sure whether there really has been a shift or not; there’s a big observational bias from the fact that I used to be one of those young folks, and now I am a wise old head. (Old, anyway.) But it’s completely plausible. Is it a bad thing?

There’s an argument to be made that widespread agreement with a basic paradigm is actually a good thing. People agree on what the important questions are and how to go about answering them. Ideas are held to a higher standard. Furthermore, it would be very hard to blame a young scientist who wanted to play by the rules rather than rocking the boat. It’s easy to say “challenge conventional wisdom!”, but the thing about conventional wisdom in a mature field is that it’s usually right. The exceptions are important and memorable (remember when everyone thought the cosmological constant was zero?), but most controversial new ideas are just wrong. Being wrong is an important part of the progress of science, but it’s hard to tell other people that they should be wrong more often.

At the end of the day, though, I agree with the spirit of Peter’s lament. I do think that the discourse within cosmology has become tamer and less willing to try out new ideas. Dark matter is well-established empirically, but we certainly don’t know that it’s WIMPs (or even axions). Inflation has had some successes, but we are very far indeed from knowing that it happened (and the problems with eternal inflation and predictability are extremely real). I have my own prejudices about what’s settled and what are interesting open questions, but the field would be healthier if youngsters would challenge people like me and make up their own minds.

Then again, you gotta eat. People need jobs and all that. I can’t possibly blame anyone who loves science and chooses to research ideas that are established and have a high probability of yielding productive results. The real responsibility shouldn’t be on young people to be bomb-throwers; it should be on the older generation, who need to be willing to occasionally take a bomb to the face, and even thank the bomb-thrower for making the effort. Who knows when an explosion might unearth some unexpected treasure?

Talking Back to Your Elders Read More »

59 Comments

Are Dark Matter Particles Lighter Than We Thought?

July 25, 2013 / 18 Comments

The 2010’s is known among the cognoscenti as the Dark Matter Decade. At least among those cognoscenti who are optimists by nature. After years of effort, experimentalists have improved the reach of their detectors to the point where we might be close to directly detecting dark matter (DM) particles — at least if the DM falls into the Weakly Interacting Massive Particle paradigm, or comes close to it for some reason. (Not every dark matter model does; axions are the obvious counterexample.) Jennifer summarizes the current situation in the latest issue of Quanta; some previous updates are from Matt Strassler and Résonaances.

There are two things going on. One is that the experiments, which look for energy being deposited by a (rare but predictable) interaction between dark matter particles and atomic nuclei, are now cutting into large regions of the predicted parameter space for weakly-interacting dark matter. So if the DM is WIMP-like, we have a great chance of seeing it before the decade is out.

The other is that there are already some hints that we have seen something. But those hints are confusing. It’s unclear whether they amount to the first tentative glimpses of most of the matter in the universe, or just statistical fluctuations in the detectors.

Here’s a figure summarizing the situation, adapted from a paper earlier this year from the CDMS experiment.

The horizontal axis is the mass of the DM particle in GeV (where a proton is about 1 GeV). The vertical axis is the strength with which the DM interacts with a proton or neutron. Lines are limits; anything above the line is supposedly ruled out. Colored regions are possible signals, if we optimistically interpret some of the data. The various limits come from CDMS’s Silicon detectors, CDMS’s Germanium detectors, a CDMS low-threshold analysis, EDELWEISS, XENON10, and XENON100. The possible signals come from CDMS’s Silicon detectors, DAMA, CoGeNT, and CRESST.

You can see why the purported hints are confusing. For one thing, they don’t really agree with each other (although they’re not too far apart). More importantly, the possible signals are apparently ruled out by some of the limits! XENON, in particular, seems incompatible even with CoGeNT and CDMS, while practically everything is incompatible with DAMA and CRESST. And no, you’re not reading the labels wrong; the recent CDMS results from their Silicon detectors are quoted both as a limit and as a signal. They see three events, where they would expect to see less than one. So the limits are what we can infer if those events are just a fluke, while the blue region is the best fit if they are actually dark matter.

Even though the various possible detections don’t completely agree with each other, they do share an intriguing property: they are pointing roughly to DM masses in the 5-15 GeV range. That is not where most people would have expected to find the dark matter. The mass isn’t precisely predicted, but typical WIMP models have masses in the 100-500 GeV range. So if this is indeed the dark matter, it’s noticeably lighter than people would have guessed. On the other hand, and in part because it’s not what was expected, it’s also a region of parameter space where the experiments are just a bit less reliable. It’s not too hard to imagine that there are backgrounds we haven’t completely taken into account, which would give the same kind of events that you might attribute to light dark matter. Rest assured that the experimenters are all over this issue.

Finally, there’s something potentially very intriguing about light dark matter. Remember that there’s about five or six times as much dark matter (by mass density) than ordinary matter in the universe. And almost all the mass of ordinary matter is in the form of nucleons (protons and neutrons). So if the dark matter particle is actually five or six GeV, it’s conceivable that there is precisely one dark matter particle per ordinary particle in the universe. And if that’s true, it’s irresistible to imagine that the origin of dark matter is somehow tied to the origin of ordinary matter — more particularly, to the asymmetry of matter and antimatter. If you could cook up a theory (and people have certainly been trying) where the dark particles carried anti-baryon number, the world would be a very interesting place. (Not that it’s not interesting already, but we would have an extra glimpse into just how interesting it is.)

Are Dark Matter Particles Lighter Than We Thought? Read More »

18 Comments