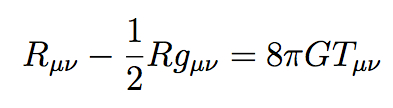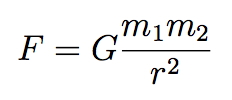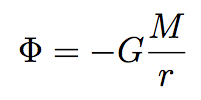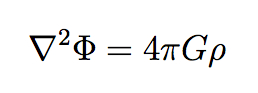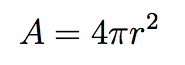Each year, the 14th of March is celebrated by scientifically-minded folks for two good reasons. First, it’s Einstein’s birthday (happy 135th, Albert!). Second, it’s Pi Day, because 3/14 is the closest calendrical approximation we have to the decimal expansion of pi, π =3.1415927….
Both of these features — Einstein and pi — are loosely related by playing important roles in science and mathematics. But is there any closer connection?
Of course there is. We need look no further than Einstein’s equation. I mean Einstein’s real equation — not E=mc2, which is perfectly fine as far as it goes, but a pretty straightforward consequence of special relativity rather than a world-foundational relationship in its own right. Einstein’s real equation is what you would find if you looked up “Einstein’s equation” in the index of any good GR textbook: the field equation relating the curvature of spacetime to energy sources, which serves as the bedrock principle of general relativity. It looks like this:
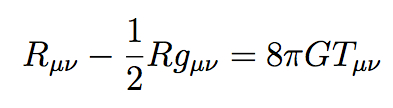
It can look intimidating if the notation is unfamiliar, but conceptually it’s quite simple; if you don’t know all the symbols, think of it as a little poem in a foreign language. In words it is saying this:
(gravity) = 8 π G × (energy and momentum).
Not so scary, is it? The amount of gravity is proportional to the amount of energy and momentum, with the constant of proportionality given by 8πG, where G is a numerical constant.
Hey, what is π doing there? It seems a bit gratuitous, actually. Einstein could easily have defined a new constant H simply be setting H=8πG. Then he wouldn’t have needed that superfluous 8π cluttering up his equation. Did he just have a special love for π, perhaps based on his birthday?
The real story is less whimsical, but more interesting. Einstein didn’t feel like inventing a new constant because G was already in existence: it’s Newton’s constant of gravitation, which makes perfect sense. General relativity (GR) is the theory that replaces Newton’s version of gravitation, but at the end of the day it’s still gravity, and it has the same strength that it always did.
So the real question is, why does π make an appearance when we make the transition from Newtonian gravity to general relativity?
Well, here’s Newton’s equation for gravity, the famous inverse square law:
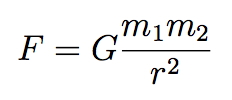
It’s actually similar in structure to Einstein’s equation: the left hand side is the force of gravity between two objects, and on the right we find the masses m1 and m2 of the objects in question, as well as the constant of proportionality G. (For Newton, mass was the source of gravity; Einstein figured out that mass is just one form of energy, and upgraded the source of gravity to all forms of energy and momentum.) And of course we divide by the square of the distance r between the two objects. No π’s anywhere to be found.
It’s a great equation, as physics equations go; one of the most influential in the history of science. But it’s also a bit puzzling, at least philosophically. It tells a story of action at a distance — two objects exert a gravitational force on each other from far away, without any intervening substance. Newton himself considered this to be an unacceptable state of affairs, although he didn’t really have a good answer:
That Gravity should be innate, inherent and essential to Matter, so that one body may act upon another at a distance thro’ a Vacuum, without the Mediation of any thing else, by and through which their Action and Force may be conveyed from one to another, is to me so great an Absurdity that I believe no Man who has in philosophical Matters a competent Faculty of thinking can ever fall into it.
But there is an answer to this conundrum. It’s to shift one’s focus from the force of gravity, F, to the gravitational potential field, Φ (Greek letter “phi”), from which the force can be derived. The field Φ fills all of space, taking some specific value at every point. In the vicinity of a single body of mass M, the gravitational potential field is given by this equation:
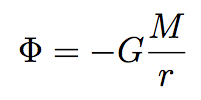
This equation bears a close resemblance to Newton’s original one. It depends inversely on the distance, rather than the distance squared, because it’s not the gravitational force directly; the force is given by the derivative (slope) of the field, which turns 1/r into 1/r2.
That’s nice, since we’ve replaced the spookiness of action at a distance with the pleasantly mechanical notion of a field filling all of space. Still no π’s, though.
But our equation only tells us what happens when we have a single body with mass M. What if we have many objects, each creating its own gravitational field, or for that matter a gas or fluid spread throughout some region? Then we need to talk about the mass density, or the amount of mass per each little volume of space, conventionally denoted ρ (Greek letter “rho”). And indeed there is an equation that relates the gravitational potential field to an arbitrary mass density spread throughout space, known as Poisson’s equation:
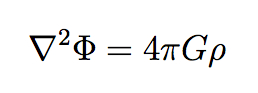
The upside-down triangle is the gradient operator (here squared to make the Laplacian); it’s a fancy three-dimensional way of saying how the field is changing through space (its vectorial derivative). But even more exciting, π has now appeared on the right-hand side! Why is that?
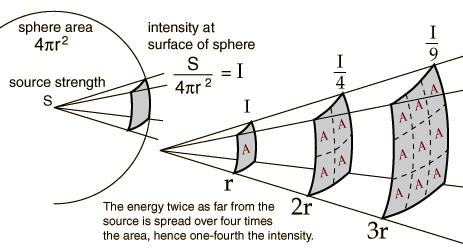
There is a technical mathematical explanation, of course, but here is the rough physical explanation. Whereas we were originally concerned (in Newton’s equation or the first equation for Φ) with the gravitational effect of a single body at a distance r, we’re now adding up all the accumulated effects of everything in the universe. That “adding up” (integrating) can be broken into two steps: (1) add up all the effects at some fixed distance r, and (2) add up the effects from all distances. In that first step, all the points at some distance r from any fixed location define a sphere centered on that location. So we’re really adding up effects spread over the area of a sphere. And the formula for the area of a sphere, of course, is:
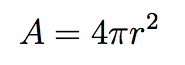
Seems almost too trivial, but that’s really the answer. The reason π comes into Poisson’s equation and not Newton’s is that Newton cared about the force between two specific objects, while Poisson tells us how to calculate the potential as a function of a matter density spread all over the place, and in three dimensions “all over the place” means “all over the area of a sphere” and then “adding up each sphere.” (We add up spheres, rather than cubes or whatever, because spheres describe fixed distances from the point of interest, and gravity depends on distance.) And the area of a sphere, just like the circumference of a circle, is proportional to π.
So then what about Einstein? Back in Newtonian gravity, it was often convenient to use the gravitational potential field, but it wasn’t really necessary; you could always in principle calculate the gravitational force directly. But when Einstein formulated general relativity, the field concept became absolutely central. The thing one calculates is not the force due to gravity (indeed, there’s a sense in which gravity isn’t really a “force” in general relativity), but rather the geometry of spacetime. That is fixed by the metric tensor field, a complicated beast that includes as a subset what we call the gravitational potential field. Einstein’s equation is directly analogous to Poisson’s equation, not to Newton’s.
So that’s the Einstein-Pi connection. Einstein figured out that gravity is best described by a field theory rather than as a direct interaction between individual bodies, and connecting fields to localized bodies involves integrating over the surface of a sphere, and the area of a sphere is proportional to π. The whole birthday thing is just a happy accident.