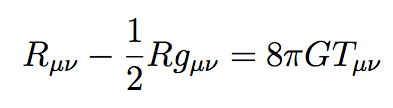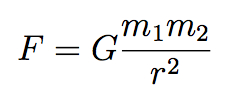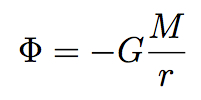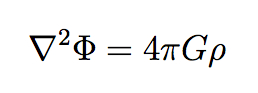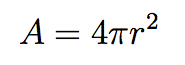Joe Polchinski’s Memories, and a Mark Wise Movie
Joe Polchinski, a universally-admired theoretical physicist at the Kavli Institute for Theoretical Physics in Santa Barbara, recently posted a 150-page writeup of his memories of doing research over the years.
Memories of a Theoretical Physicist
Joseph PolchinskiWhile I was dealing with a brain injury and finding it difficult to work, two friends (Derek Westen, a friend of the KITP, and Steve Shenker, with whom I was recently collaborating), suggested that a new direction might be good. Steve in particular regarded me as a good writer and suggested that I try that. I quickly took to Steve’s suggestion. Having only two bodies of knowledge, myself and physics, I decided to write an autobiography about my development as a theoretical physicist. This is not written for any particular audience, but just to give myself a goal. It will probably have too much physics for a nontechnical reader, and too little for a physicist, but perhaps there with be different things for each. Parts may be tedious. But it is somewhat unique, I think, a blow-by-blow history of where I started and where I got to. Probably the target audience is theoretical physicists, especially young ones, who may enjoy comparing my struggles with their own. Some disclaimers: This is based on my own memories, jogged by the arXiv and Inspire. There will surely be errors and omissions. And note the title: this is about my memories, which will be different for other people. Also, it would not be possible for me to mention all the authors whose work might intersect mine, so this should not be treated as a reference work.
As the piece explains, it’s a bittersweet project, as it was brought about by Joe struggling with a serious illness and finding it difficult to do physics. We all hope he fully recovers and gets back to leading the field in creative directions.
I had the pleasure of spending three years down the hall from Joe when I was a postdoc at the ITP (it didn’t have the “K” at that time). You’ll see my name pop up briefly in his article, sadly in the context of an amusing anecdote rather than an exciting piece of research, since I stupidly spent three years in Santa Barbara without collaborating with any of the brilliant minds on the faculty there. Not sure exactly what I was thinking.
Joe is of course a world-leading theoretical physicist, and his memories give you an idea why, while at the same time being very honest about setbacks and frustrations. His style has never been to jump on a topic while it was hot, but to think deeply about fundamental issues and look for connections others have missed. This approach led him to such breakthroughs as a new understanding of the renormalization group, the discovery of D-branes in string theory, and the possibility of firewalls in black holes. It’s not necessarily a method that would work for everyone, especially because it doesn’t necessarily lead to a lot of papers being written at a young age. (Others who somehow made this style work for them, and somehow survived, include Ken Wilson and Alan Guth.) But the purity and integrity of Joe’s approach to doing science is an example for all of us.
Somehow over the course of 150 pages Joe neglected to mention perhaps his greatest triumph, as a three-time guest blogger (one, two, three). Too modest, I imagine.
His memories make for truly compelling reading, at least for physicists — he’s an excellent stylist and pedagogue, but the intended audience is people who have already heard about the renormalization group. This kind of thoughtful but informal recollection is an invaluable resource, as you get to see not only the polished final product of a physics paper, but the twists and turns of how it came to be, especially the motivations underlying why the scientist chose to think about things one way rather than some other way.
(Idea: there is a wonderful online magazine called The Players’ Tribune, which gives athletes an opportunity to write articles expressing their views and experiences, e.g. the raw feelings after you are traded. It would be great to have something like that for scientists, or for academics more broadly, to write about the experiences [good and bad] of doing research. Young people in the field would find it invaluable, and non-scientists could learn a lot about how science really works.)
You also get to read about many of the interesting friends and colleagues of Joe’s over the years. A prominent one is my current Caltech colleague Mark Wise, a leading physicist in his own right (and someone I was smart enough to collaborate with — with age comes wisdom, or at least more wisdom than you used to have). Joe and Mark got to know each other as postdocs, and have remained friends ever since. When it came time for a scientific gathering to celebrate Joe’s 60th birthday, Mark contributed a home-made movie showing (in inimitable style) how much progress he had made over the years in the activities they had enjoyed together in their relative youth. And now, for the first time, that movie is available to the whole public. It’s seven minutes long, but don’t make the mistake of skipping the blooper reel that accompanies the end credits. Many thanks to Kim Boddy, the former Caltech student who directed and produced this lost masterpiece.
When it came time for his own 60th, Mark being Mark he didn’t want the usual conference, and decided instead to gather physicist friends from over the years and take them to a local ice rink for a bout of curling. (Canadian heritage showing through.) Joe being Joe, this was an invitation he couldn’t resist, and we had a grand old time, free of any truly serious injuries.

We don’t often say it out loud, but one of the special privileges of being in this field is getting to know brilliant and wonderful people, and interacting with them over periods of many years. I owe Joe a lot — even if I wasn’t smart enough to collaborate with him when he was down the hall, I learned an enormous amount from his example, and often wonder how he would think about this or that issue in physics.
Joe Polchinski’s Memories, and a Mark Wise Movie Read More »