Guest Post

Usually, technical advances in mathematical physics don’t generate a lot of news buzz. But last year a story in Quanta proved to be an exception. It relayed the news of an intriguing new way to think about quantum field theory — a mysterious mathematical object called the Amplituhedron, which gives a novel perspective on how we think about the interactions of quantum fields.

This is cutting-edge stuff at the forefront of modern physics, and it’s not an easy subject to grasp. Natalie Wolchover’s explanation in Quanta is a great starting point, but there’s still a big gap between a popular account and the research paper, in this case by Nima Arkani-Hamed and Jaroslav Trnka. Fortunately, Jaroslav is now a postdoc here at Caltech, and was willing to fill us in on a bit more of the details.

“Halfway between a popular account and a research paper” can still be pretty forbidding for the non-experts, but hopefully this guest blog post will convey some of the techniques used and the reasons why physicists are so excited by these (still very tentative) advances. For a very basic overview of Feynman diagrams in quantum field theory, see my post on effective field theory.

---

I would like to thank Sean to give me an opportunity to write about my work on his blog. I am happy to do it, as the new picture for scattering amplitudes I have been looking for in last few years just recently crystalized in the object we called Amplituhedron, emphasizing its connection to both scattering amplitudes and the generalization of polyhedra. To remind you, “amplitudes” in quantum field theory are functions that we square to get probabilities in scattering experiments, for example that two particles will scatter and convert into two other particles.

Despite the fact that I will talk about some specific statements for scattering amplitudes in a particular gauge theory, let me first mention the big picture motivation for doing this. Our main theoretical tool in describing the microscopic world is Quantum Field Theory (QFT), developed more than 60 years ago in the hands of Dirac, Feynman, Dyson and others. It unifies quantum mechanics and special theory of relativity in a consistent way and it has been proven to be an extremely successful theory in countless number of cases. However, over the past 25 years there has been an increasing evidence that the standard definition of QFT using Lagrangians and Feynman diagrams does not exhibit simplicity and sometimes even hidden symmetries of the final result. This has been most dramatically seen in calculation of scattering amplitudes, which are basic objects directly related to probabilities in scattering experiments. For a very nice history of the field look at the blog post by Lance Dixon who recently won together with Zvi Bern and David Kosower the Sakurai prize. There are also two nice popular articles by Natalie Wolchover – on the Amplituhedron and also the progress of understanding amplitudes in quantum gravity.

The Lagrangian formulation of QFT builds on two pillars: locality and unitarity, which means that the particle interactions are point-like and sum of the probabilities in scattering experiments must be equal to one. The underlying motivation of my work is a very ambitious attempt to reformulate QFT using a different set of principles and see locality and unitarity emerge as derived properties. Obviously I am not going to solve this problem but rather concentrate on a much simpler problem whose solution might have some features that can be eventually generalized. In particular, I will focus on on-shell (“real” as opposed to “virtual”) scattering amplitudes of massless particles in a “supersymmetric cousin” of Quantum Chromodynamics (theory which describes strong interactions) called N=4 Super Yang-Mills theory (in planar limit). It is a very special theory sometimes referred as “Simplest Quantum Field Theory” because of its enormous amount of symmetry. If there is any chance to pursue our project further we need to do the reformulation for this case first.

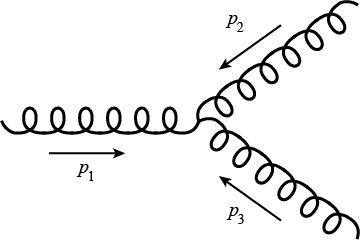
Feynman diagrams give us rules for how to calculate an amplitude for any given scattering process, and these rules are very simple: draw all diagrams built from vertices given by the Lagrangian and evaluate them using certain rules. This gives a function M of external momenta and helicities (which is spin for massless particles). The Feynman diagram expansion is perturbative, and the leading order piece is always captured by tree graphs (no loops). Then we call M a tree amplitude, which is a rational function of external momenta and helicities. In particular, this function only depends on scalar products of momenta and polarization vectors. The simplest example is the scattering of three gluons,

represented by a single Feynman diagram.

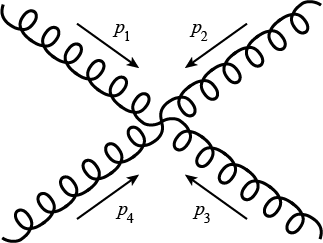
Amplitudes for more than three particles are sums of Feynman diagrams which have internal lines represented by factors P^2 (where P is the sum of momenta) in the denominator. For example, one part of the amplitude for four gluons (2 gluons scatter and produce another 2 gluons) is

Higher order corrections are represented by diagrams with loops which contain unfixed momenta – called loop momenta – we need to integrate over, and the final result is represented by more complicated functions – polylogarithms and their generalizations. The set of functions we get after loop integrations are not known in general (even for lower loop cases). However, there exists a simpler but still meaningful function for loop amplitudes – the integrand, given by a sum of all Feynman diagrams before integration. This is a rational function of helicities and momenta (both external and loop momenta) and it has many nice properties which are similar to tree amplitudes. Tree amplitudes and Integrand of loop amplitudes are objects of our interest and I will call them just “amplitudes” in the rest of the text.

While we already have a new picture for them, we can use the top-bottom approach and phrase the problem in the following way: We want to find a mathematical question to which the amplitude is the answer.

As a first step, we need to characterize how the amplitude is invariantly defined in a traditional way. The answer is built in the standard formulation of QFT: the amplitude is specified by properties of locality and unitarity, which translate to simple statements about poles (these are places where the denominator goes to zero). In particular, all poles of M must be sums of external (for integrand also loop) momenta and on these poles M must factorize in a way which is dictated by unitarity. For large class of theories (including our model) this is enough to specify M completely. Reading backwards, if we find a function which satisfies these properties it must be equal to the amplitude. This is a crucial point for us and it guarantees that we calculate the correct object.

Now we consider completely unrelated geometry problem: we define a new geometrical shape – the Amplituhedron. It is something like multi-dimensional polygon embedded in a particular geometrical space, called the Grassmannian. This has a very good motivation in the work done by me and my collaborators in last 5 years on relation between Grassmannians and amplitudes, but I will not explain it here in more details as it would need a separate blog post. Importantly, we can prove that the expression we get for a volume of this object satisfies properties mentioned above and therefore, we can conclude that the scattering amplitudes in our theory are directly related to the volume of Amplituhedron.

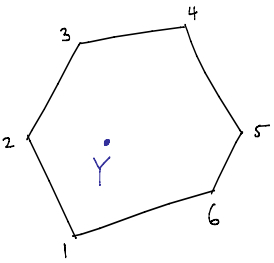This is a basic picture of the whole story but I will try to elaborate it a little more. Many features of the story can be show on a simple example of polygon which is also a simple version of Amplituhedron. Let us consider n points in a (projective) plane and draw a polygon by connecting them in a given ordering. In order to talk about the interior the polygon must be convex which puts some restrictions on these n vertices. Our object is then specified as a set of all points inside a convex polygon.

Now, we want to generalize it to Grassmannian. Instead of points we consider lines, planes, and in general k-planes inside a convex hull (generalization of polygon in higher dimensions). The geometry notion of being “inside” does not really generalize beyond points but there is a precise algebraic statement which directly generalizes from points to k-planes. It is a positivity condition on a matrix of coefficients that we get if we expand a point inside a polygon as linear combination of vertices. In the end, we can define a space of Amplituhedron in the same way as we defined a convex polygon by putting constraints on its vertices (which generalizes convexity) and also positivity conditions on the k-plane (which generalizes notion being inside). In general, there is not a single Amplituhedron but it is rather labeled by three indices: n,k,l. Here n stands for the number of particles, which is equal to a number of vertices, index k captures the helicity structure of the amplitude and it defines a dimensionality of a k-plane which defines a space. Finally, l is the number of loops which translates to the number of lines we have in our configuration space in addition to the k-plane. In the next step we define a volume, more precisely it is a form with logarithmic singularities on the boundaries of this space, and we can show that this function satisfies exactly the same properties as the scattering amplitude. For more details you can read our original paper.

This is a complete reformulation we were looking for. In the definition we do not talk about Lagrangians, Feynman diagrams or locality and unitarity. Our definition is purely geometrical with no reference to physical concepts which all emerge from the shape of Amplituhedron.

Having this definition in hand does not give the answer for amplitudes directly, but it translates the physics problem to purely math problem – calculating volumes. Despite the fact that this object has not been studied by mathematicians at all (there are recent works on the positive Grassmannian of which the Amplituhedron is a substantial generalization), it is reasonable to think that this problem might have a nice general solution which would provide all-loop order results.

There are two main directions in generalization of this story. The first is to try to extend the picture to full (integrated) amplitudes rather than just an integrand. This would definitely require more complicated mathematical structures as would deal now with polylogarithms and their generalizations rather than rational functions. However, already now we have some evidence that the story should extend there as well. The other even more important direction is to generalize this picture to other Quantum field theories. The answer is unclear but if it is positive the picture would need some substantial generalization to capture richness of other QFTs which are absent in our model (like renormalization).

The story of Amplituhedron has an interesting aspect which we always emphasized as a punchline of this program: emergence of locality and unitarity from a shape of this geometrical object, in particular from positivity properties that define it. Of course, amplitudes are local and unitary but this construction shows that these properties might not be fundamental, and can be replaced by a different set of principles from which locality and unitarity follow as derived properties. If this program is successful it might be also an important step to understand quantum gravity. It is well known that quantum mechanics and gravity together make it impossible to have local observables. It is conceivable that if we are able to formulate QFT in the language that does not make any explicit reference to locality, the weak gravity limit of the theory of quantum gravity might land us on this new formulation rather than on the standard path integral formulation. This would not be the first time when the reformulation of the existing theory helped us to do the next step in our understanding of Nature. While Newton’s laws are manifestly deterministic, there is a completely different formulation of classical mechanics – in terms of the principle of the least action – which is not manifestly deterministic. The existence of these very different starting points leading to the same physics was somewhat mysterious to classical physicists, but today we know why the least action formulation exists: the world is quantum-mechanical and not deterministic, and for this reason, the classical limit of quantum mechanics can’t immediately land on Newton’s laws, but must match to some formulation of classical physics where determinism is not a central but derived notion. The least action principle formulation is thus much closer to quantum mechanics than Newton’s laws, and gives a better jumping off point for making the transition to quantum mechanics as a natural deformation, via the path integral.

We may be in a similar situation today. If there is a more fundamental description of physics where space-time and perhaps even the usual formulation of quantum mechanics don’t appear, then even in the limit where non-perturbative gravitational effects can be neglected and the physics reduces to perfectly local and unitary quantum field theory, this description is unlikely to directly reproduce the usual formulation of field theory, but must rather match on to some new formulation of the physics where locality and unitarity are derived notions. Finding such reformulations of standard physics might then better prepare us for the transition to the deeper underlying theory.

The hunt for dark matter has been heating up once again, driven (as usual) by tantalizing experimental hints. This time the hints are coming mainly from outer space rather than underground laboratories, which makes them harder to check independently, but there’s a chance something real is going on. We need more data to be sure, as scientists have been saying since the time Eratosthenes measured the circumference of the Earth.

As I mentioned briefly last week, Katherine Freese of the University of Michigan has a new book coming out, The Cosmic Cocktail, that deals precisely with the mysteries of dark matter. Katie was also recently at the UCLA Dark Matter Meeting, and has agreed to share some of her impressions with us. (She also insisted on using the photo on the right, as a way of reminding us that this is supposed to be fun.)

---

Dark Matter Everywhere (at the biannual UCLA Dark Matter Meeting)

The UCLA Dark Matter Meeting is my favorite meeting, period. It takes place every other year, usually at the Marriott Marina del Rey right near Venice Beach, but this year on UCLA campus. Last week almost two hundred people congregated, both theorists and experimentalists, to discuss our latest attempts to solve the dark matter problem. Most of the mass in galaxies, including our Milky Way, is not comprised of ordinary atomic material, but instead of as yet unidentified dark matter. The goal of dark matter hunters is to resolve this puzzle. Experimentalist Dave Cline of the UCLA Physics Department runs the dark matter meeting, with talks often running from dawn till midnight. Every session goes way over, but somehow the disorganization leads everybody to have lots of discussion, interaction between theorists and experimentalists, and even more cocktails. It is, quite simply, the best meeting. I am usually on the organizing committee, and cannot resist sending in lots of names of people who will give great talks and add to the fun.

Last week at the meeting we were treated to multiple hints of potential dark matter signals. To me the most interesting were the talks by Dan Hooper and Tim Linden on the observations of excess high-energy photons — gamma-rays — coming from the Central Milky Way, possibly produced by annihilating WIMP dark matter particles. (See this arxiv paper.) Weakly Interacting Massive Particles (WIMPs) are to my mind the best dark matter candidates. Since they are their own antiparticles, they annihilate among themselves whenever they encounter one another. The Center of the Milky Way has a large concentration of dark matter, so that a lot of this annihilation could be going on. The end products of the annihilation would include exactly the gamma-rays found by Hooper and his collaborators. They searched the data from the FERMI satellite, the premier gamma-ray mission (funded by NASA and DoE as well as various European agencies), for hints of excess gamma-rays. They found a clear excess extending to about 10 angular degrees from the Galactic Center. This excess could be caused by WIMPs weighing about 30 GeV, or 30 proton masses. Their paper called these results “a compelling case for annihilating dark matter.” After the talk, Dave Cline decided to put out a press release from the meeting, and asked the opinion of us organizers. Most significantly, Elliott Bloom, a leader of the FERMI satellite that obtained the data, had no objection, though the FERMI team itself has as yet issued no statement.

Many putative dark matter signals have come and gone, and we will have to see if this one holds up. Two years ago the 130 GeV line was all the rage — gamma-rays of 130 GeV energy that were tentatively observed in the FERMI data towards the Galactic Center. (Slides from Andrea Albert’s talk.) This line, originally proposed by Stockholm’s Lars Bergstrom, would have been the expectation if two WIMPs annihilated directly to photons. People puzzled over some anomalies of the data, but with improved statistics there isn’t much evidence left for the line. The question is, will the 30 GeV WIMP suffer the same fate? As further data come in from the FERMI satellite we will find out.

What about direct detection of WIMPs? Laboratory experiments deep underground, in abandoned mines or underneath mountains, have been searching for direct signals of astrophysical WIMPs striking nuclei in the detectors. At the meeting the SuperCDMS experiment hammered on light WIMP dark matter with negative results. The possibility of light dark matter, that was so popular recently, remains puzzling. 10 GeV dark matter seemed to be detected in many underground laboratory experiments: DAMA, CoGeNT, CRESST, and in April 2013 even CDMS in their silicon detectors. Yet other experiments, XENON and LUX, saw no events, in drastic tension with the positive signals. (I told Rick Gaitskell, a leader of the LUX experiment, that I was very unhappy with him for these results, but as he pointed out, we can’t argue with nature.) Last week at the conference, SuperCMDS, the most recent incarnation of the CDMS experiment, looked to much lower energies and again saw nothing. (Slides from Lauren Hsu’s talk.) The question remains: are we comparing apples and oranges? These detectors are made of a wide variety of types of nuclei and we don’t know how to relate the results. Wick Haxton’s talk surprised me by discussion of nuclear physics uncertainties I hadn’t been aware of, that in principle could reconcile all the disagreements between experiments, even DAMA and LUX. Most people think that the experimental claims of 10 GeV dark matter are wrong, but I am taking a wait and see attitude.

We also heard about the hints of detection of a completely different dark matter candidate: sterile neutrinos. (Slides from George Fuller’s talk.) In addition to the three known neutrinos of the Standard Model of Particle Physics, there could be another one that doesn’t interact with the standard model. Yet its decay could lead to x-ray lines. Two separate groups found indications of lines in data from the Chandra and XMM-Newton space satellites that would be consistent with a 7 keV neutrino (7 millionths of a proton mass). Could it be that there is more than one type of dark matter particle? Sure, why not?

On the last evening of the meeting, a number of us went to the Baja Cantina, our favorite spot for margaritas. Rick Gaitskell was smart: he talked us into the $60.00 pitchers, high enough quality that the 6AM alarm clocks the next day (that got many of us out of bed and headed to flights leaving from LAX) didn’t kill us completely. We have such a fun community of dark matter enthusiasts. May we find the stuff soon!

This year’s Sakurai Prize of the American Physical Society, one of the most prestigious awards in theoretical particle physics, has been awarded to Zvi Bern, Lance Dixon, and David Kosower “for pathbreaking contributions to the calculation of perturbative scattering amplitudes, which led to a deeper understanding of quantum field theory and to powerful new tools for computing QCD processes.” An “amplitude” is the fundamental thing one wants to calculate in quantum mechanics — the probability that something happens (like two particles scattering) is given by the amplitude squared. This is one of those topics that is absolutely central to how modern particle physics is done, but it’s harder to explain the importance of a new set of calculational techniques than something marketing-friendly like finding a new particle. Nevertheless, the field pioneered by Bern, Dixon, and Kosower made a splash in the news recently, with Natalie Wolchover’s masterful piece in Quanta about the “Amplituhedron” idea being pursued by Nima Arkani-Hamed and collaborators. (See also this recent piece in Scientific American, if you subscribe.)

I thought about writing up something about scattering amplitudes in gauge theories, similar in spirit to the post on effective field theory, but quickly realized that I wasn’t nearly familiar enough with the details to do a decent job. And you’re lucky I realized it, because instead I asked Lance Dixon if he would contribute a guest post. Here’s the result, which sets a new bar for guest posts in the physics blogosphere. Thanks to Lance for doing such a great job.

—————————————————————-

“Amplitudes: The untold story of loops and legs”

Sean has graciously offered me a chance to write something about my research on scattering amplitudes in gauge theory and gravity, with my longtime collaborators, Zvi Bern and David Kosower, which has just been recognized by the Sakurai Prize for theoretical particle physics.

In short, our work was about computing things that could in principle be computed with Feynman diagrams, but it was much more efficient to use some general principles, instead of Feynman diagrams. In one sense, the collection of ideas might be considered “just tricks”, because the general principles have been around for a long time. On the other hand, they have provided results that have in turn led to new insights about the structure of gauge theory and gravity. They have also produced results for physics processes at the Large Hadron Collider that have been unachievable by other means.

The great Russian physicist, Lev Landau, a contemporary of Richard Feynman, has a quote that has been a continual source of inspiration for me: “A method is more important than a discovery, since the right method will lead to new and even more important discoveries.”

The work with Zvi and David, which has spanned two decades, is all about scattering amplitudes, which are the complex numbers that get squared in quantum mechanics to provide probabilities for incoming particles to scatter into outgoing ones. High energy physics is essentially the study of scattering amplitudes, especially those for particles moving very close to the speed of light. Two incoming particles at a high energy collider smash into each other, and a multitude of new, outgoing particles can be created from their relativistic energy. In perturbation theory, scattering amplitudes can be computed (in principle) by drawing all Feynman diagrams. The first order in perturbation theory is called tree level, because you draw all diagrams without any closed loops, which look roughly like trees. For example, one of the two tree-level Feynman diagrams for a quark and a gluon to scatter into a W boson (carrier of the weak force) and a quark is shown here.

We write this process as qg → Wq. To get the next approximation (called NLO) you do the one loop corrections, all diagrams with one closed loop. One of the 11 diagrams for the same process is shown here.

Then two loops (one diagram out of hundreds is shown here), and so on.

The forces underlying the Standard Model of particle physics are all described by gauge theories, also called Yang-Mills theories. The one that holds the quarks and gluons together inside the proton is a theory of “color” forces called quantum chromodynamics (QCD). The physics at the discovery machines called hadron colliders — the Tevatron and the LHC — is dominantly that of QCD. Feynman rules, which assign a formula to each Feynman diagram, have been known since Feynman’s work in the 1940s. The ones for QCD have been known since the 1960s. Still, computing scattering amplitudes in QCD has remained a formidable problem for theorists.

Back around 1990, the state of the art for scattering amplitudes in QCD was just one loop. It was also basically limited to “four-leg” processes, which means two particles in and two particles out. For example, gg → gg (two gluons in, two gluons out). This process (or reaction) gives two “jets” of high energy hadrons at the Tevatron or the LHC. It has a very high rate (probability of happening), and gives our most direct probe of the behavior of particles at very short distances.

Another reaction that was just being computed at one loop around 1990 was qg → Wq (one of whose Feynman diagrams you saw earlier). This is another copious process and therefore an important background at the LHC. But these two processes are just the tip of an enormous iceberg; experimentalists can easily find LHC events with six or more jets (http://arxiv.org/abs/arXiv:1107.2092, http://arxiv.org/abs/arXiv:1110.3226, http://arxiv.org/abs/arXiv:1304.7098), each one coming from a high energy quark or gluon. There are many other types of complex events that they worry about too.

A big problem for theorists is that the number of Feynman diagrams grows rapidly with both the number of loops, and with the number of legs. In the case of the number of legs, for example, there are only 11 Feynman diagrams for qg → Wq. One diagram a day, and you are done in under two weeks; no problem. However, if you want to do instead the series of processes: qg → Wqg, qg → Wqgg, qg → Wqggg, qg → Wqgggg, you face 110, 1253, 16,648 and 256,265 Feynman diagrams. That could ruin your whole decade (or more). [See the figure; the ring-shaped blobs stand for the sum of all one-loop Feynman diagrams.]

It’s not just the raw number of diagrams. Many of the diagrams with large numbers of external particles are much, much messier than the 11 diagrams for qg → Wq. Plus the messy diagrams tend to be numerically unstable, causing problems when you try to get numbers out. This problem definitely calls out for a new method.

Why care about all these scattering amplitudes at all? …

Guest Post: Lance Dixon on Calculating AmplitudesRead More »

In the last post I suggested that nobody should come to these parts looking for insight into the kind of work that was just rewarded with the 2012 Nobel Prize in Physics. How wrong I was! True, you shouldn’t look to me for such things, but we were able to borrow an expert from a neighboring blog to help us out. John Preskill is the Richard P. Feynman Professor of Theoretical Physics (not a bad title) here at Caltech. He was a leader in quantum field theory for a long time, before getting interested in quantum information theory and becoming a leader in that. He is part of Caltech’s Institute for Quantum Information and Matter, which has started a fantastic new blog called Quantum Frontiers. This is a cross-post between that blog and ours, but you should certainly be checking out Quantum Frontiers on a regular basis.

---

When I went to school in the 20th century, “quantum measurements” in the laboratory were typically performed on ensembles of similarly prepared systems. In the 21st century, it is becoming increasingly routine to perform quantum measurements on single atoms, photons, electrons, or phonons. The 2012 Nobel Prize in Physics recognizes two of the heros who led these revolutionary advances, Serge Haroche and Dave Wineland. Good summaries of their outstanding achievements can be found at the Nobel Prize site, and at Physics Today.

Serge Haroche developed cavity quantum electrodynamics in the microwave regime. Among other impressive accomplishments, his group has performed “nondemolition” measurements of the number of photons stored in a cavity (that is, the photons can be counted without any of the photons being absorbed). The measurement is done by preparing a Rubidium atom in a superposition of two quantum states. As the Rb atom traverses the cavity, the energy splitting of these two states is slightly perturbed by the cavity’s quantized electromagnetic field, resulting in a detectable phase shift that depends on the number of photons present. (Caltech’s Jeff Kimble, the Director of IQIM, has pioneered the development of analogous capabilities for optical photons.)

Dave Wineland developed the technology for trapping individual atomic ions or small groups of ions using electromagnetic fields, and controlling the ions with laser light. His group performed the first demonstration of a coherent quantum logic gate, and they have remained at the forefront of quantum information processing ever since. They pioneered and mastered the trick of manipulating the internal quantum states of the ions by exploiting the coupling between these states and the quantized vibrational modes (phonons) of the trapped ions. They have also used quantum logic to realize the world’s most accurate clock (17 decimal places of accuracy), which exploits the frequency stability of an aluminum ion by transferring its quantum state to a magnesium ion that can be more easily detected with lasers. This clock is sensitive enough to detect the slowing of time due to the gravitational red shift when lowered by 30 cm in the earth’s gravitational field.

With his signature mustache and self-effacing manner, Dave Wineland is not only one of the world’s greatest experimental physicists, but also one of the nicest. His brilliant experiments and crystal clear talks have inspired countless physicists working in quantum science, not just ion trappers but also those using a wide variety of other experimental platforms.

Dave has spent most of his career at the National Institute of Standards and Technology (NIST) in Boulder, Colorado. I once heard Dave say that he liked working at NIST because “in 30 years nobody told me what to do.” I don’t know whether that is literally true, but if it is even partially true it may help to explain why Dave joins three other NIST-affiliated physicists who have received Nobel Prizes: Bill Phillips, Eric Cornell, and “Jan” Hall.

I don’t know Serge Haroche very well, but I once spent a delightful evening sitting next to him at dinner in an excellent French restaurant in Leiden. The occasion, almost exactly 10 years ago, was a Symposium to celebrate the 100th anniversary of H. A. Lorentz’s Nobel Prize in Physics, and the dinner guests (there were about 20 of us) included the head of the Royal Dutch Academy of Sciences and the Rector Magnificus of the University of Leiden (which I suppose is what we in the US would call the “President”). I was invited because I happened to be a visiting professor in Leiden at the time, but I had not anticipated such a classy gathering, so had not brought a jacket or tie. When I realized what I had gotten myself into I rushed to a nearby store and picked up a tie and a black V-neck sweater to pull over my levis, but I was under-dressed to put it mildly. Looking back, I don’t understand why I was not more embarrassed.

Anyway, among other things we discussed, Serge filled me in on the responsibilities of a Professor at the College de France. It’s a great honor, but also a challenge, because each year one must lecture on fresh material, without repeating any topic from lectures in previous years. In 2001 he had taught quantum computing using my online lecture notes, so I was pleased to hear that I had eased his burden, at least for one year.

On another memorable occasion, Serge and I both appeared in a panel discussion at a conference on quantum computing in 1996, at the Institute for Theoretical Physics (now the KITP) in Santa Barbara. Serge and a colleague had published a pessimistic article in Physics Today: Quantum computing: dream or nightmare? In his remarks for the panel, he repeated this theme, warning that overcoming the damaging effects of decoherence (uncontrolled interactions with the environment which make quantum systems behave classically, and which Serge had studied experimentally in great detail) is a far more daunting task than theorists imagined. I struck a more optimistic note, hoping that the (then) recently discovered principles of quantum error correction might be the sword that could slay the dragon. I’m not sure how Haroche feels about this issue now. Wineland, too, has often cautioned that the quest for large-scale quantum computers will be a long and difficult struggle.

This exchange provided me with an opportunity to engage in some cringe-worthy rhetorical excess when I wrote up a version of my remarks. Having (apparently) not learned my lesson, I’ll quote the concluding paragraph, which somehow seems appropriate as we celebrate Haroche’s and Wineland’s well earned prizes:

“Serge Haroche, while a leader at the frontier of experimental quantum computing, continues to deride the vision of practical quantum computers as an impossible dream that can come to fruition only in the wake of some as yet unglimpsed revolution in physics. As everyone at this meeting knows well, building a quantum computer will be an enormous technical challenge, and perhaps the naysayers will be vindicated in the end. Surely, their skepticism is reasonable. But to me, quantum computing is not an impossible dream; it is a possible dream. It is a dream that can be held without flouting the laws of physics as currently understood. It is a dream that can stimulate an enormously productive collaboration of experimenters and theorists seeking deep insights into the nature of decoherence. It is a dream that can be pursued by responsible scientists determined to explore, without prejudice, the potential of a fascinating and powerful new idea. It is a dream that could change the world. So let us dream.”

If you happen to have been following developments in quantum gravity/string theory this year, you know that quite a bit of excitement sprang up over the summer, centered around the idea of “firewalls.” The idea is that an observer falling into a black hole, contrary to everything you would read in a general relativity textbook, really would notice something when they crossed the event horizon. In fact, they would notice that they are being incinerated by a blast of Hawking radiation: the firewall.

This claim is a daring one, which is currently very much up in the air within the community. It stems not from general relativity itself, or even quantum field theory in a curved spacetime, but from attempts to simultaneously satisfy the demands of quantum mechanics and the aspiration that black holes don’t destroy information. Given the controversial (and extremely important) nature of the debate, we’re thrilled to have Joe Polchinski provide a guest post that helps explain what’s going on. Joe has guest-blogged for us before, of course, and he was a co-author with Ahmed Almheiri, Donald Marolf, and James Sully on the paper that started the new controversy. The dust hasn’t yet settled, but this is an important issue that will hopefully teach us something new about quantum gravity.

---

Introduction

Thought experiments have played a large role in figuring out the laws of physics. Even for electromagnetism, where most of the laws were found experimentally, Maxwell needed a thought experiment to complete the equations. For the unification of quantum mechanics and gravity, where the phenomena take place in extreme regimes, they are even more crucial. Addressing this need, Stephen Hawking’s 1976 paper “Breakdown of Predictability in Gravitational Collapse” presented one of the great thought experiments in the history of physics. …

Guest Post: Joe Polchinski on Black Holes, Complementarity, and FirewallsRead More »

When it comes to microwaves from the sky, the primordial cosmic background radiation gets most of the publicity, while everything that originates nearby is lumped into the category of “foregrounds.” But those foregrounds are interesting in their own right; they tell us about important objects in the universe, like our own galaxy. For nearly a decade, astronomers have puzzled over a mysterious hazy glow of microwaves emanating from the central region of the Milky Way. More recently, gamma-ray observations have revealed a related set of structures known as “Fermi Bubbles.” We’re very happy to host this guest post by Douglas Finkbeiner from Harvard, who has played a crucial role in unraveling the mystery.

---

Planck, Gamma-ray Bubbles, and the Microwave Haze

“Error often is to be preferred to indecision” — Aaron Burr, Jr.

Among the many quotes that greet a visitor to the Frist Campus Center at Princeton University, this one is perhaps the most jarring. These are bold words from the third Vice President of the United States, the man who shot Alexander Hamilton in a duel. Yet they were on my mind as a postdoc in 2003 as I considered whether to publish a controversial claim: that the microwave excess called the “haze” might originate from annihilating dark matter particles. That idea turned out to be wrong, but pursuing it was one of the best decisions of my career.

In 2002, I was studying the microwave emission from tiny, rapidly rotating grains of interstellar dust. This dust spans a range of sizes from microscopic flecks of silicate and graphite, all the way down to hydrocarbon molecules with perhaps 50 atoms. In general these objects are asymmetrical and have an electric dipole, and a rotating dipole emits radiation. Bruce Draine and Alex Lazarian worked through this problem at Princeton in the late 1990s and found that the smallest dust grains can rotate about 20 billion times a second. This means the radiation comes out at about 20 GHz, making them a potential nuisance for observations of the cosmic microwave background. However, by 2003 there was still no convincing detection of this “spinning dust” and many doubted the signal would be strong enough to be observed.

The haze

In February 2003, the Wilkinson Microwave Anisotropy Probe (WMAP) team released their first results. …

Guest Post: Doug Finkbeiner on Fermi Bubbles and Microwave HazeRead More »