Conservation of energy is a somewhat sacred principle in physics, though it can be tricky in certain circumstances, such as an expanding universe. Quantum mechanics is another context in which energy conservation is a subtle thing — so much so that it’s still worth writing papers about, which Jackie Lodman and I recently did. In this blog post I’d like to explain two things:
- In the Many-Worlds formulation of quantum mechanics, the energy of the wave function of the universe is perfectly conserved. It doesn’t “require energy to make new universes,” so that is not a respectable objection to Many-Worlds.
- In any formulation of quantum mechanics, energy doesn’t appear to be conserved as seen by actual observers performing quantum measurements. This is a not-very-hard-to-see aspect of quantum mechanics, which nevertheless hasn’t received a great deal of attention in the literature. It is a phenomenon that should be experimentally observable, although as far as I know it hasn’t yet been; we propose a simple experiment to do so.
The first point here is well-accepted and completely obvious to anyone who understands Many-Worlds. The second is much less well-known, and it’s what Jackie and I wrote about. I’m going to try to make this post accessible to folks who don’t know QM, but sometimes it’s hard to make sense without letting the math be the math.
First let’s think about energy in classical mechanics. You have a system characterized by some quantities like position, momentum, angular momentum, and so on, for each moving part within the system. Given some facts of the external environment (like the presence of gravitational or electric fields), the energy is simply a function of these quantities. You have for example kinetic energy, which depends on the momentum (or equivalently on the velocity), potential energy, which depends on the location of the object, and so on. The total energy is just the sum of all these contributions. If we don’t explicitly put any energy into the system or take any out, the energy should be conserved — i.e. the total energy remains constant over time.
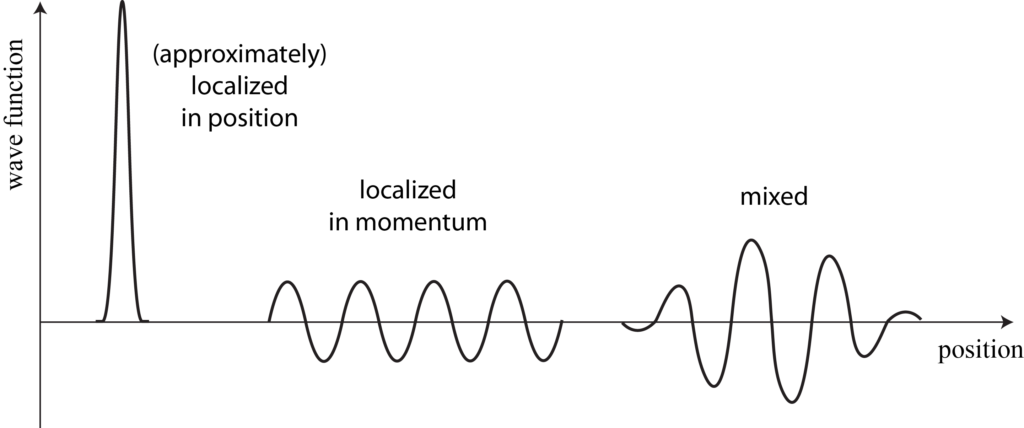
There are two main things you need to know about quantum mechanics. First, the state of a quantum system is no longer specified by things like “position” or “momentum” or “spin.” Those classical notions are now thought of as possible measurement outcomes, not well-defined characteristics of the system. The quantum state — or wave function — is a superposition of various possible measurement outcomes, where “superposition” is a fancy term for “linear combination.”
Consider a spinning particle. By doing experiments to measure its spin along a certain axis, we discover that we only ever get two possible outcomes, which we might call “spin-up” or “
” and “spin-down” or “
.” But before we’ve made the measurement, the system can be in some superposition of both possibilities. We would write 
, the wave function of the spin, as
![\[ (\Psi) = a(\uparrow) + b(\downarrow), \]](https://www.preposterousuniverse.com/blog/wp-content/ql-cache/quicklatex.com-99680f4c2d2711403d8013da6c15e01f_l3.png "Rendered by QuickLaTeX.com")
where 
and 
are numerical coefficients, the “amplitudes” corresponding to spin-up and spin-down, respectively. (They will generally be complex numbers, but we don’t have to worry about that.)
The second thing you have to know about quantum mechanics is that measuring the system changes its wave function. When we have a spin in a superposition of this type, we can’t predict with certainty what outcome we will see. All we can predict is the probability, which is given by the amplitude squared. And once that measurement is made, the wave function “collapses” into a state that is purely what is observed. So we have
![\[ (\Psi)_\mathrm{post-measurement} = \begin{cases} (\uparrow), & \mbox{with probability } |a|^2,\\ (\downarrow), & \mbox{with probability } |b|^2. \end{cases}\]](https://www.preposterousuniverse.com/blog/wp-content/ql-cache/quicklatex.com-8107a4b9ad0ecdf4d1c5352831392591_l3.png "Rendered by QuickLaTeX.com")
At least, that’s what we teach our students — Many-Worlds has a slightly more careful story to tell, as we’ll see.
We can now ask about energy, but the concept of energy in quantum mechanics is a bit different from what we are used to in classical mechanics. Classically, a single particle has a constant energy, given by the sum of its potential energy (which depends on its position) and its kinetic energy (which depends on its momentum). But in quantum mechanics, the state of the particle isn’t specified by position and velocity; those are just possible measurement outcomes. The state of the system is given by the wave function.
There are, however, special states called eigenstates, in which some particular observable has a definite value. So we have “position eigenstates,” for which the position is exactly defined, “momentum eigenstates,” for which momentum is exactly defined, and so on. There are no states for which both position and momentum are exactly defined — that would violate the Heisenberg uncertainty principle. And indeed, in most states neither one of them is exactly defined. But we can think of any state as a superposition of position eigenstates, or as a superposition of momentum eigenstates (but not both).
The same goes for energy, which is an observable quantity just like position or momentum. There are energy eigenstates, where the energy has a definite value, but neither position nor momentum do. And if you happen to be in an energy eigenstate, “energy conservation” is trivially true — the energy stays the same. But that’s a much less interesting statement than in classical mechanics, because energy eigenstates don’t evolve at all! A system with a definite energy just sits there, stationary and unevolving.
Fortunately, most states don’t have a definite energy, but rather are superpositions of different energy eigenstates. That’s good, because the system as a whole can then evolve. All the interesting evolution of quantum systems can actually be thought of as different energy eigenstates combining to give time-dependent answers to questions we could ask about other quantities like position or momentum.
But what can we say about energy conservation if a quantum state doesn’t even have a definite energy? Well, we can still associate an average energy 
to any particular quantum state, even if specific measurements might give answers that fluctuate around that central value. (For experts: the expectation value of the Hamiltonian.) If we think of an arbitrary quantum state as a weighted superposition of various specific-energy eigenstates, the average energy is just what it sounds like: the weighted average of the energies of all those eigenstates.
Let’s imagine that we’re in the state described above, a superposition of spin-up and spin-down. And let’s further imagine that the spin-up state is a state with definite energy (i.e. it’s an energy eigenstate) 
, and the spin-down state has a definite energy 
. Then the average energy is just a combination of both these values, weighted by the squares of the amplitudes:
![\[ \bar{E} = |a|^2E_\uparrow + |b|^2 E_\downarrow.\]](https://www.preposterousuniverse.com/blog/wp-content/ql-cache/quicklatex.com-5fc68edfbcd29b175a5d7a90f1601ce1_l3.png "Rendered by QuickLaTeX.com")
As long as the quantum system obeys the Schrödinger equation, you will be happy to hear that the average energy is precisely conserved. It doesn’t change over time. That’s the notion of “energy conservation” you have in quantum mechanics: the average or expected value stays constant, as long as you obey the Schrödinger equation.
Alas, there is a famous case in which quantum systems do not obey the Schrödinger equation, or at least they appear not to: when they are being measured. As we said above, what we teach our students is that wave functions collapse when they are observed; this collapse process is unpredictable, and doesn’t obey the Schrödinger equation. As a result, the average energy is not conserved in the process of quantum measurement. Indeed, as we can quickly see by comparing with the equations we started with, after we do the measurement the system will either have energy (if we measured spin-up) or it will have energy (if we measured spin-down). And in general, if those two values are unequal (and both and are non-zero), neither one of those will be the same as our original average .
This is all pretty straightforward, almost trivial! And indeed, I wouldn’t object if you thought that. But people like energy conservation, deep in their bones. So what I suspect is that, if you asked most working quantum physicists what was going on here, they would guess that the total energy of the universe actually is conserved, but you just weren’t keeping track of it accurately. After all, there needs to be some apparatus and observer who interact with the system in order to measure it. Perhaps whenever the energy changes in the system we observe, there is a compensating change in energy in the apparatus or the rest of the world, so that the total is conserved.
Not so, or at least not in quantum mechanics as we generally understand it. That’s what we show in the paper Jackie and I recently submitted.
Energy Non-Conservation in Quantum Mechanics
Sean M. Carroll and Jackie Lodman
We study the conservation of energy, or lack thereof, when measurements are performed in quantum mechanics. The expectation value of the Hamiltonian of a system can clearly change when wave functions collapse in accordance with the standard textbook (Copenhagen) treatment of quantum measurement, but one might imagine that the change in energy is compensated by the measuring apparatus or environment. We show that this is not true; the change in the energy of a state after measurement can be arbitrarily large, independent of the physical measurement process. In Everettian quantum theory, while the expectation value of the Hamiltonian is conserved for the wave function of the universe (including all the branches), it is not constant within individual worlds. It should therefore be possible to experimentally measure violations of conservation of energy, and we suggest an experimental protocol for doing so.
Basically what we do is to construct a complete toy model of both a system and a measuring apparatus, one sufficiently simple that we can keep track of the energy exactly. And we verify that the change in energy of the system has no necessary connection at all to the change in energy of the rest of the world. (As we explain in the paper, other people have pointed to this phenomenon before, but usually in the context of trying to avoid it; we are more celebratory, and suggest that people should be looking for this experimentally.)
So, if you’re a textbook/Copenhagen kind of person, the punchline is simple: energy is not conserved in quantum measurements. Really the only way out is to refuse to accept the “average energy” of a state as representing the true energy at all. That’s fine, as far as it goes. But in that case almost no states (i.e., no states other than energy eigenstates) will have a well-defined energy. And as we say in the paper, the average energy is a rigorous energy-like quantity that would be perfectly conserved if it weren’t for measurements. So the fact that measurements violate that conservation law is pretty interesting.
Now we can come to the Everettian perspective, which puts a very attractive spin on things. I won’t go too deeply into the Everettian formulation itself; see this delightful book, or this somewhat shorter blog post. The point is that in Everett, wave functions never collapse; all they ever do is obey the Schrödinger equation. What you and I think of as a “measurement” is just when a quantum system in a superposition becomes entangled with some macroscopic object (the “measuring apparatus”), which in turn becomes entangled with its environment (“decoherence”). When that happens, the different parts of the superposition become parts of separate worlds. So rather than our above superposition of spin-up and spin-down suddenly collapsing into one or the other, the state evolves smoothly into one describing two non-interacting copies of reality, one where the spin is up and the other where the spin is down.
The nice thing about this is: energy is completely conserved! Individual observers think that they witness the average energy changing, because they only live in one branch at a time. But in the “wave function of the universe” (the quantum state describing all branches at once), the average energy is a constant, since that wave function obeys the Schrödinger equation. The energy simply gets divided up between branches slightly differently as time goes on.
This story is very different than what you might often hear, namely that it’s Everett, not Copenhagen, that has a problem with energy conservation. After all, where does the energy come from to make all those worlds?
Hopefully this worry has been completely dissipated by the discussion above. The point is that there are two different senses of the word “energy”: the energy that observers within any branch (world) might attribute to the reality they see, and the total energy of all the branches combined. If a wave function describes a collection of many branches labeled 
, with amplitudes 
and average energies 
, the average energy of the whole shebang is
![\[\bar{E} = |a_1|^2E_1 + |a_2|^2E_2 + \cdots.\]](https://www.preposterousuniverse.com/blog/wp-content/ql-cache/quicklatex.com-402a83b1f1362789079af46a185e285a_l3.png "Rendered by QuickLaTeX.com")
So even though there are more and more branches as time evolves, the contribution of each branch to the total energy is weighted by the factors 
, and those numbers go down over time as branches split. The effects precisely cancel, so that the total energy of the universe (all branches included) is constant. It’s just that individual branches get “thinner” over time (their amplitudes get smaller), so they make smaller and smaller contributions to the total.
This “thinning” process is completely invisible from inside. You have no way of knowing what the amplitude of your particular branch is; it’s invisible to you. The fact that the amplitudes go down doesn’t mean that the world around you looks somehow less tangible or energetic. The energy you would calculate by adding up the individual energies of all the stuff in the universe (stars, planets, black holes, dark matter, etc) goes into the energy of your particular branch; there’s no reason for that number to systematically diminish over time. (Given the tiny changes in average energy that can happen at measurement events, the energy of your world as seen from inside will undergo a gradual random walk of gradually-diminishing steps, but honestly the changes are so incredibly tiny that you’d never notice.)
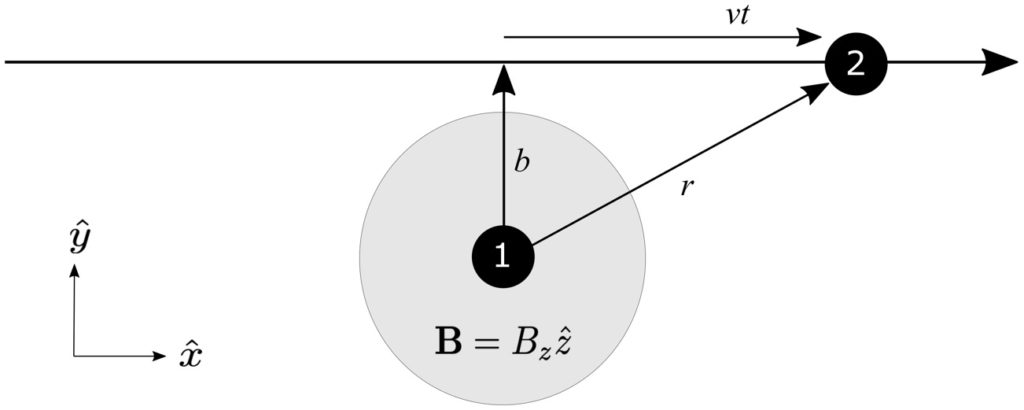
Is this change of the average energy of the universe (as seen by observers on individual branches) potentially observable in experiments? In principle, absolutely yes; in practice, maybe, but it would be hard. Not particle-accelerator-the-size-of-the-galaxy hard, but a challenge. This is the other thing that Jackie and I suggest in our paper. The trick is that (1) it’s extremely hard in practice to construct superpositions of very different energy states, so any hoped-for changes in average energy will be very tiny; and (2) any measurement generally spills a lot of energy all over the place, which is hard to keep track of. I won’t go into details, but we suggest a general protocol, and also a specific implementation where one spinning particle is kept stationary in a trap, while another travels by it and they become entangled. Then by measuring the spin of the moving particle, we can change the spin of the stationary one, hopefully changing its energy in the process.
I’m honestly not sure how feasible this kind of experiment is; that’s above my pay grade. But it’s a nice example of how thinking carefully about the foundations of quantum mechanics can lead to interesting ideas.
Great stuff! Is it possible to formulate this in terms of entropy? Inuitively, I think of the ever increasing number of Everettian branches as analogous to the ever increasing entropy of the universe. That makes me wonder if entanglement IS entropy increase (or is related in some other way) and, similarly, if “local” fluctuations in energy (on one Everettian branch) is similar to local fluctuations in entropy.
This question may be incredibly stupid as my formal study of quantum mechanics goes back to the previous millennium. Basically, my question is since we need to square a wave function to get a probability distribution, that means the wave function is the square root of the probability distribution, which has no correlation in reality that I can think of. So, since wave mechanics and matrix mechanics were shown to be equivalent, are these both just mathematical constructs that get us to physical reality (the probabilities) but are non-sensical when trying to make physical sense of what they represent, like complex numbers were thought to be until they found correlations between them and natural behaviors.
I do appreciate all you do for those of us struggling to keep up. You clearly are good at what you do.
Steve Ruis
Retired Professor of Chemistry
The trouble with all this is it doesn’t make sense to talk about the expectation value of the Hamiltonian with respect to a linear superposition as representing any kind of an energy of it, any more than it does to talk about the expectation value of the position operator for a state as representing its position.
Regarding MWI, what is it that actually delineates the amplitudes associated with the branches as the wave function splits off?
If the average energy of all branches is conserved, but the distribution of energy between branches could be unequal, then it’s possible that some few branchings are very unequal, even though for the most part the differences between branches are extremely small. There might exist universes descended from branches that are preponderately from the deficient side of gazillion branchings since the universe began, resulting in a universe with considerably less energy than its ancient ancestral parent. What effect, cosmologically speaking, might this have on observations of events in the distant past, such as those apparent in the CBR?
“no states other than energy eigenstates will have a well-defined energy” isn’t that perfectly reasonable? And not just for energy, but for every other physical observable too.
What will happen to the Scrödinger Wave Equation once it’s compatible with QG?
Do Physicists that prefer the Everettian view have any ideas.?
Interesting paper. I think (but am not sure) that I understand the general thrust.
I guess a key assumption is that the global universe is not in an energy eigenstate, which you justify by saying that, well, we see things happen so this must be true. But there are long-standing ideas that if you are within a quantum state, you can be in a stationary state and see have the illusion of dynamics- this is the Page-Wootters mechanism. Could this provide a loophole?
The violation of conservation laws by quantum measurements goes back to Wigner and subsequent refinement as the Wigner–Araki–Yanase theorem. It sets limits on how precise a measurement can be given a conservation law. You seem to be taking the complementary approach and asking how much violation of a conservation law can you get in a precise measurement. Do this fit together with the WAY theorem?
“… if those two values are unequal (and both a and b are non-zero), neither one of those will be the same as our original average \bar E”
Is it possible in this example that the collapse of the wavefunction is contingent on attaining energy conservation (i.e., E(post-measurement) = E(average pre-measurement) forcing either a = 0 or b = 0 at collapse)?
So, does this blog post and paper say the summation of the Everettian *IS* Newtonian (the energy is the energy, and is conserved), in a way Copenhagen can’t? (Remember the Can’t!)
I’ve always thought of Many Worlds as the “easy” way to view QM, but as otherwise equivalent to Copenhagen once the math is done. This shows me the benefit of Many Worlds isn’t merely that it is easier to comprehend, but that it actually makes the physics make sense, without the proverbial “and then something magical happens” step when quantum systems interact during measurement.
Am I getting the right gist from this?
What happened to the last sentence of the Arxiv PDF Acknowledgements?
Very interesting paper! Issues pointed out by Sean & Jackie in their arxiv paper are surely major hindrances to actual experimental demonstration of energy non-conservation. That’s why I think a different approach may be required. In particular, I think we need to show that a particular measurable phenomenon that we do observe would be actually impossible unless there was energy non-conservation (of course, within the framework of Standard Model).
This is above my pay grade too, but I note that from a naive view energy is conserved in quantum mechanics. Since it is a relativistic theory it aims to conserve laws such as conservation of energy. Specifically here quantum field theory integrates the Lagrangian density to get the action, so both energy and time are conserved. (I hadn’t thought of it, but classically you would add complementarity of energy and time to the dynamical complementarities of say momentum and position and now I see one reason why.)
I’m thus going to naively differ on some points and agree on others, since bringing in the unnecessary axiomatic machinery of “interpretations” and “wavefunctions of the universe” on top of the minimal and working “shut up and calculate” Copenhagen will result in that. And precisely quantum physics warns us, based on observations, against assuming extraneous (hidden) parameters.
I don’t see any problem with universal conservation of energy in a flat universe. The usual problem seems to be that general relativity doesn’t allow you to localize energy in all topologies, but here the energy density is zero over sufficiently large volumes by Einstein’s equations on a perfect fluid (gas) filled universe so there is no such problem. E.g. Wilczek’s path integral core theory [“The World of Everyday Experience, In One Equation” @ Preposterous Universe] works fine with localized additive fields, and could include both a slow roll scalar inflation field [“Planck 2018 results X. Constraints on inflation”, Planck Collaboration, A&A, 2020] and a tensor gravity field [“Quantum gravity as a low energy effective field theory”, John Donoghue, Scholarpedia, 2017] with no energy conservation problem.
There are many reasons why the observed flat universe of modern inflationary hot big bang cosmology seems reasonable to me, but here I’ll just point out that it gives us an immediate consistency test. An indefinite era of vacuum of a quantum inflation field is also zero energy density.
Returning to the claim that energy isn’t conserved during wavefunction collapse, it is akin to asking for wavefunction or state conservation in the same manner. I have to agree with you as well as Somdatta Bhattacharya that it doesn’t make obvious sense to talk of the expectation value of a superposition in this case. It is the same problem with mass in quantum gravity field theory above.
But, and I believe it is the 2nd time I relate to this paper that fit my naive taste, it looks like one can accept the wavefunction collapse as a relativistic effect from conserving the Planck constant in the same way that length contraction and time dilation is [“Answering Mermin’s challenge with conservation per no preferred reference frame”, Stuckey at al, Nature Scientific Reports, 2020]. Then in the same way that a consideration of a theory of a wavefunction of the universe would Monte Carlo sample outcomes to reconstruct the average energy after collapse I’m guessing we could do the same by repeating observations in quantum field physics.
I spotted the joker in your experiment (section III of the paper).
You are trying start with a system in an (approximate) energy eigenstate and then split the Universe into a high energy and a low energy branch, showing non-conservation.
You think your experiment does this by
1) Take an unpolarized proton. Since it is in a field-free region, the energy is not split based on the (mixed state) proton spin direction.
2) embed the proton in a magnetic field
3) measure the spin along the B-field direction, which can be done with arbitrarily low energy transfer
4) the Universe branch where the spin is up has a different energy than the branch where the spin is down.
However, when you do 2) you are entangling spin of the proton with the energy of the system that embeds the proton in the magnetic field.
If you call the magnetic field embedding system M which is in an initial state |M_0> then you go from
(a|↑>+b|↓>)|M_0>
before the embedding to
a|↑ M_↑>+b|↓ M_↓>
after the embedding, where M_↑ is the state of M after a spin-up proton has been inflicted on it.
Measuring the proton spin state tells you whether you are in the up-branch |↑ M_↑> or the down-branch.
However, both the up-branch and the down-branch have the same energy, because whatever energy difference there is in the proton is found in the opposite direction in M.[1] Thus if you start in an ~energy eigenstate, you end up in an ~energy eigenstate with no change in energy within any branch.
So energy is conserved in each branch of the universe.
[1] If the energy of M did not depend on whether it is used on a spin-up or a spin-down proton, then you could make a deterministic perpetual energy source (or its opposite) by just feeding it a steady diet of polarized protons and pulling out the spin-flip energy.
David, we thought of that worry (footnote on p. 6), but I don’t think it’s true. The spin of the proton won’t back-react so noticeably on the magnetic field that the two components have the same energy. If it did, spins wouldn’t precess in magnetic fields. (And what is the principle according to which the magnetic-field energy must exactly match the spin-coupling energy?)
And you can’t deterministically pull out the higher-energy component, for the same reason you can’t ever deterministically get one particular measurement outcome for a quantity that is in a superposition. Otherwise who needs to go to all this trouble — just take any system that is not in an energy eigenstate, and magically project onto high-energy components.
I do think that (1) our toy model in section II establishes beyond reasonable doubt that the effect is real, and (2) that our proposed experiment in section III is very likely not the most practical way to see it. I’m hoping that someone comes up with more feasible proposals.
“Then in the same way that a consideration of a theory of a wavefunction of the universe would Monte Carlo sample outcomes to reconstruct the average energy after collapse I’m guessing we could do the same by repeating observations in quantum field physics.”
Ha! Like the ‘old’ adage you know: “Anything a wavefunction of the universe can do, wavefunction collapse can do simpler.” 😉
Sean,
If you have a 2.3 tonne 26 Tesla magnet that you are doing the experiment with, then the spin of the proton won’t back-react ‘noticeably’ compared to however many megajoules you are storing in the field. However it will back-react by an amount of energy equal to the spin-flip energy.
(For the sake of this discussion, all conductors are super, all batteries are perfectly rechargeable, and all permanent magnets are eternal)
In the classical world, you can take a permanent bar magnet and put it in a solenoid and push current into it, where a given absolute value of current will give a field stronger or weaker depending on whether the solenoid and bar magnet fields are parallel or antiparallel. The electrical energy you put in (integrated current times back-EMF) is equal to the total change in energy the solenoid and magnet system ends up with which is different for the two cases. If you are using a battery-powered system you can drain the solenoid and charge your battery back up to its initial 100% state in either case. (If you flip the magnet when the solenoid is charged, the exerted or released mechanical energy to do this shows up as a difference in battery charge after draining the solenoid.) (I haven’t actually done the calculation that proves the equality, but the lack of working perpetual motion machines is pretty good evidence.)
This holds true if the permanent magnet is a proton whose spin is aligned with solenoid axis. It may require a zeptovoltmeter with a google-to-one dynamic range to measure the difference in back-EMF, but it is there.
So skipping to the quantum world, when you take a proton in a mixed state and put in the solenoid, your zeptovoltmeter will give you one of two values, which gives you a measurement of the proton spin, and that measurement tells you which branch you are now in.
Then you disconnect the zeptovoltmeter and make sure you have no other way of doing the measurement. When you turn on the current, your magnet is entangled with the proton spin as discussed in my previous comment. The universe doesn’t branch until you measure the spin, and that also tells you how much charge is left in your battery. But in either branch, the total energy is the same and you can drain the solenoid and get the battery back to 100%. Energy is conserved.
If this were not the case, then you could chose to put a pure ↑ proton in your apparatus and get the battery to 101%.
As for precession: that is if you have B field parallel to +Z and the proton has a prepared spin parallel to +X. With a fixed period the proton spin goes to +Y, -X, -Y, +X and repeats. The states among which it precesses all have the same energy spectrum.
David– To keep things simple, let’s just focus on the precession question. You claim that 1) the proton becomes maximally entangled with the magnetic field, in a state a|↑ M_↑>+b|↓ M_↓>, and 2) that the energy of the magnetic-field states exactly compensates that of the proton, so that the two terms in this superposition are both energy eigenstates with equal energy E. I don’t see why either one of those should be true, but let’s grant them for now.
Then both states evolve simply by picking up a multiplicative phase, exp{-i E t}. Since that phase is the same for both components, it’s just an overall common factor, and irrelevant to the dynamics. The system as a whole is entirely stationary, nothing physical is changing with time. So how can there be precession? (Usually precession happens because the spin-up and spin-down components are thought to have different energies, and therefore different phase factors, and therefore real time-dependent evolution.)
OK, I see where you were going with the precession example. In the conventional case of a proton in an external field, the field is not coherently entangled with the proton spin, and precession does occur.[1]
In my reply, M is the entire Mechanism which subjects the proton to the magnetic field. Consider the following cycle:
0) Prepare an original state where the proton is a pure-state ↑ in a field-free region, with the Mechanism in its ground state M_0.
1) Operate the Mechanism to get a ↑ in a field.
2) Flip the spin to ↓ and harvest the released energy.
3) Operate the Mechanism in reverse to get a ↓ in a field-free region.
4) Flip the spin (at no energy cost) and you are back in the original state 0), ready to repeat the cycle.
Each time through the cycle you harvest the spin-flip energy. Since this is all pure states only one Universe branch is involved, and you presumably believe that energy is conserved (no perpetual motion allowed if you aren’t branching). You deduce that it takes one spin-flip of net energy to operate the Mechanism forwards on a ↑ and in reverse on a ↓. (And zero net energy to operate both forwards and backwards on ↓.)
Therefore, you deduce that the Mechanism states M_↑ and M_↓ differ in energy by one spin-flip.
In other words, the two states |↑ M_↑> and |↓ M_↓> have the same total energy.
Therefore if you start with an unpolarized mixed state proton and the Mechanism in ground state
(a|↑>+b|↓>)|M_0>
then when you operate the mechanism forward
a|↑ M_↑>+b|↓ M_↓>
both a and b give you the same energy, and when you measure the spin to branch the Universe, both branches end up with the same amount of energy.
In other words, if you can’t violate energy conservation when you know the spin, you can’t violate it when you don’t know the spin.
[1] Very off-topic and nothing to do with this discussion, here is an example of a maximally entangled field that doesn’t cause precession. Start with a superconducting loop with zero current, and an unpolarized proton far away. Move the proton into the loop. The induced current and consequent magnetic field of the loop are maximally entangled with the proton spin. By symmetry, both spin-up and spin-down states have the same energy, and therefore no differential phase change and no precession.
If the system you observe plus the measurement aparatus plus the environment, i.e. the wave function of your toy universe as a whole, obeys some kind of Schrödinger equation (with a Hermitian Hamiltonian to be precise), then the whole shebang – as you call it – must be time-reversible. Do we have any experimental facts that underpin the assumption a measurement might be reversible?
David, I’m confused. The experiment we are proposing involves precisely “the conventional case of a proton in an external field, the field is not coherently entangled with the proton spin, and precession does occur.” In that case you don’t have a state a|↑ M_↑>+b|↓ M_↓> where both terms have the same energy. Are you suggesting that we are not allowed to start with the conventional case, for some reason?
I am saying that within each branch of the universe, energy is conserved in the entire system, where the system includes the proton, the magnetic field generator, the observer, and everything else that makes the experiment a closed, isolated system. But you have to consider all energy transfers within the system, e.g., the energy required to move the proton into the field.
If you do not consider all energy transfers and changes in the system, but only look at the energy of the proton once it is in the magnetic field, then energy is ‘not conserved’. But that is also true in the classical case. If you have a pure-state ↑ proton in a field-free region, then put it in a magnetic field, then it has a different amount of energy. If you take a rare-earth magnet in a field-free region, then put it in a magnetic field, that too changes the rare-earth magnet’s energy. Neither case violates conservation of energy.
Start with the un-Z-polarized proton (a|↑>+b|↓>) in the field-free region and with the system is originally in an energy eigenstate with energy at t=0 E_system0. (Just make a measurement the energy of the system before you start, with an accuracy that is much better than the spin-flip energy).
For book-keeping purposes you can split the energy into the energy of the ‘p’roton and the energy of the ‘r’est of the system.
E_system0 = E_p0 + E_r0
(where each component of energy and the sum is independent of the proton spin:
E_p0↑ = E_p0↓ at this time, likewise E_r0↑ = E_r0↓ and E_system0↑ = E_system0↓)
Now let the rest of the system move the proton into a magnetic field at time t=1. The rest of the system takes or releases some amount of energy that depends on the spin but (because you are not yet claiming that conservation of energy is violated) the total energy is unchanged and therefore the same for both spin states.:
E_system1↑ = E_system1↓
(E_p1↑ + E_r1↑) = (E_p1↓ + E_r1↓)
but E_p1↑ ≠ E_p1↓ and E_r1↑ ≠ E_r1↓
The energy of the proton is now in a mixed state, but the energy of the rest of the system is also in a mixed state, and the two energy states are maximally entangled.
(For your precession question: Yes, at this time the observer in the system can see the proton precess: E_p1↑ ≠ E_p1↓ so the two proton states will have changing relative phase. The rest of the system is also changing relative phase across the mixture, but the instruments aren’t looking at that.)
Now at t=2 you measure the spin of the proton to complete the experiment. With universe branching probabilities:
|a|^2: E_system2 = E_system1↑ = E_system0 ; E_p1 = E_p1↑ ; E_r1 = E_r1↑
|b|^2: E_system2 = E_system1↓ = E_system0 ; E_p1 = E_p1↓ ; E_r1 = E_r1↓
So E_system2 = E_system0 in each branch, and no observer sees any violation of energy conservation.
I hope, Sean, you are planning to respond, in a couple of weeks, once all we followers have had enough time to read and digest this blog; there seems like some great ideas out there; and you did that with the Biggest Ideas in the Universe; it really helps to cement these hard to understand concepts for us.
Classical theory stated something like energy can neither be created, nor destroyed, it only changes ‘form’—or something like that.. Some friends and I have discussed such, even though we are neither physicists nor mathematicians. I am a philosopher—an autodidact; another, psychologist, turned systems analyst; the third, a neuroscientist, formerly, physics major in school.. We play with notions about truth, infinity—other issues. On the old idea of energy: let us suppose our sun burned out. We would be iced, yes? Energy lost—to us. Other energy, in the universe would obtain—just not for us. Inasmuch as, quasi-theoretically, there must be energy , as long as there are sources for same. (stars, nebulae, gravity, black holes—whatever else…)
So, whether energy is neither created nor lost seems irrelevant.
I have written, still writing, on the truth enigma.. Story not yet finished. Fun, though.
Also have had fun with the infinity paradox: Infinity does not matter, in our current mathematics. If you cannot get there, it does not matter: there is no ‘there’ there.
Could the energy conservation on the quantum level be restored by including a quantum entanglement in the picture? If we produce two photons from an original spin-0 state, then we know that even if each of these photons individually has a random spin along any measurement axis with no hidden parameters inside (so there is classically no reason for the two random values to add up to some particular number), if we measure their spins along the same axis they will magically (by a “spooky action”) come out complementary so the total spin is conserved (zero). Now we could say the same about an energy measurement: although an outcome of an energy measurement of an individual particle is blurred by the uncertainty, there would be another particle (e.g. in the measurement apparatus, thus in the perfectly causal range) that somehow came into entanglement with a first one that – having it’s energy blurred out as well – would miraculously happen to measure to the energy value offset from it’s (classically expected) energy by amount just right to keep the total energy nicely conserved. Obviously, as the apparatus is macroscopic and so there are zillions and zillions of other particles buzzing around we can’t tell which one of them was actually entangled and restored the energy conservation. But if we could, we’d see that the total energy is conserved.