This year we give thanks for space. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, the Fourier Transform, Riemannian Geometry, the speed of light, the Jarzynski equality, and the moons of Jupiter.)
Even when we restrict to essentially scientific contexts, “space” can have a number of meanings. In a tangible sense, it can mean outer space — the final frontier, that place we could go away from the Earth, where the stars and other planets are located. In a much more abstract setting, mathematicians use “space” to mean some kind of set with additional structure, like Hilbert space or the space of all maps between two manifolds. Here we’re aiming in between, using “space” to mean the three-dimensional manifold in which physical objects are located, at least as far as our observable universe is concerned.
That last clause reminds us that there are some complications here. The three dimensions we see of space might not be all there are; extra dimensions could be hidden from us by being curled up into tiny balls (or generalizations thereof) that are too small to see, or if the known particles and forces are confined to a three-dimensional brane embedded in a larger universe. On the other side, we have intimations that quantum theories of gravity imply the holographic principle, according to which an N-dimensional universe can be thought of as arising as a projection of (N-1)-dimensions worth of information. And much less speculatively, Einstein and Minkowski taught us long ago that three-dimensional space is better thought of as part of four-dimensional spacetime.
Let’s put all of that aside. Our everyday world is accurately modeled as stuff, distributed through three-dimensional space, evolving with time. That’s something to be thankful for! But we can also wonder why it is the case.
I don’t mean “Why is space three-dimensional?”, although there is that. I mean why is there something called “space” at all? I recently gave an informal seminar on this at Columbia, and I talk about it a bit in Something Deeply Hidden, and it’s related in spirit to a question Michael Nielsen recently asked on Twitter, “Why does F=ma?”
Space is probably emergent rather than fundamental, and the ultimate answer to why it exists is probably going to involve quantum mechanics, and perhaps quantum gravity in particular. The right question is “Why does the wave function of the universe admit a description as a set of branching semi-classical worlds, each of which feature objects evolving in three-dimensional space?” We’re working on that!
But rather than answer it, for the purposes of thankfulness I just want to point out that it’s not obvious that space as we know it had to exist, even if classical mechanics had been the correct theory of the world.
Newton himself thought of space as absolute and fundamental. His ontology, as the philosophers would put it, featured objects located in space, evolving with time. Each object has a trajectory, which is its position in space at each moment of time. Quantities like “velocity” and “acceleration” are important, but they’re not fundamental — they are derived from spatial position, as the first and second derivatives with respect to time, respectively.
But that’s not the only way to do classical mechanics, and in some sense it’s not the most basic and powerful way. An alternative formulation is provided by Hamiltonian mechanics, where the fundamental variable isn’t “position,” but the combination of “position and momentum,” which together describe the phase space of a system. The state of a system at any one time is given by a point in phase space. There is a function of phase space cleverly called the Hamiltonian H(x,p), from which the dynamical equations of the system can be derived.
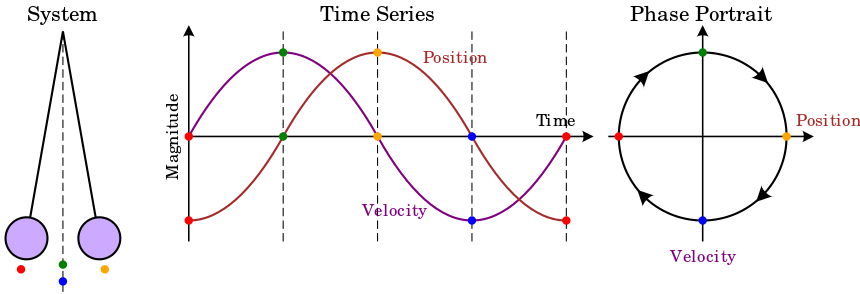
That might seem a little weird, and students tend to be somewhat puzzled by the underlying idea of Hamiltonian mechanics when they are first exposed to it. Momentum, we are initially taught in our physics courses, is just the mass times the velocity. So it seems like a derived quantity, not a fundamental one. How can Hamiltonian mechanics put momentum on an equal footing to position, if one is derived from the other?
The answer is that in the Hamiltonian approach, momentum is not defined to be mass times velocity. It ends up being equal to that by virtue of an equation of motion, at least if the Hamiltonian takes the right form. But in principle it’s an independent variable.
That’s a subtle distinction! Hamiltonian mechanics says that at any one moment a system is described by two quantities, its position and its momentum. No time derivatives or trajectories are involved; position and momentum are completely different things. Then there are two equations telling us how the position and the momentum change with time. The derivative of the position is the velocity, and one equation sets it equal to the momentum divided by the mass, just as in Newtonian mechanics. The other equation sets the derivative of the momentum equal to the force. Combining the two, we again find that force equals mass times acceleration (derivative of velocity).
So from the Hamiltonian perspective, positions and momenta are on a pretty equal footing. Why then, in the real world, do we seem to “live in position space”? Why don’t we live in momentum space?
As far as I know, no complete and rigorous answer to these questions has ever been given. But we do have some clues, and the basic principle is understood, even if some details remain to be ironed out.
That principle is this: we can divide the world into subsystems that interact with each other under appropriate circumstances. And those circumstances come down to “when they are nearby in space.” In other words, interactions are local in space. They are not local in momentum. Two billiard balls can bump into each other when they arrive at the same location, but nothing special happens when they have the same momentum or anything like that.
Ultimately this can be traced to the fact that the Hamiltonian of the real world is not some arbitrary function of positions and momenta; it’s a very specific kind of function. The ultimate expression of this kind of locality is field theory — space is suffused with fields, and what happens to a field at one point in space only directly depends on the other fields at precisely the same point in space, nowhere else. And that’s embedded in the Hamiltonian of the universe, in particular in the fact that the Hamiltonian can be written as an integral over three-dimensional space of a local function, called the “Hamiltonian density.”
![]()
where φ is the field (which here acts as a “coordinate”) and π is its corresponding momentum.
This represents progress on the “Why is there space?” question. The answer is “Because space is the set of variables with respect to which interactions are local.” Which raises another question, of course: why are interactions local with respect to anything? Why do the fundamental degrees of freedom of nature arrange themselves into this kind of very specific structure, rather than some other one?
We have some guesses there, too. One of my favorite recent papers is “Locality From the Spectrum,” by Jordan Cotler, Geoffrey Penington, and Daniel Ranard. By “the spectrum” they mean the set of energy eigenvalues of a quantum Hamiltonian — i.e. the possible energies that states of definite energy can have in a theory. The game they play is to divide up the Hilbert space of quantum states into subsystems, and then ask whether a certain list of energies is compatible with “local” interactions between those subsystems. The answers are that most Hamiltonians aren’t compatible with locality in any sense, and for those where locality is possible, the division into local subsystems is essentially unique. So locality might just be a consequence of certain properties of the quantum Hamiltonian that governs the universe.
Fine, but why that Hamiltonian? Who knows? This is above our pay grade right now, though it’s fun to speculate. Meanwhile, let’s be thankful that the fundamental laws of physics allow us to describe our everyday world as a collection of stuff distributed through space. If they didn’t, how would we ever find our keys?
I look forward to these every year. Never stop 🙂
Sean, just wanted to say that although I gave no formal training in your field (I’m 65) I have been interested in astrophysics since I was about 10(didn’t know what it was then!) & have read & learned & read & read…& I find your papers so easy to understand & your thinking easy to follow. So thank you !
Vicki Timms.
I give thanks to professor Carroll and all the others academia who have made it possible for an old firefighter like like me to start to comprehend how amazing our universe really is with out superstition .
Thanks for this, as usual! Happy Thanksgiving from Victoria, BC, in Canada (where we are way past our Thanksgiving celebrations)
I, too, give thanks for those who stretch my mind with lucid explanations. Another I enjoy is John Cook (https://www.johndcook.com/blog/).
While I always wish for more posts from Sean (please start another book…), it is always important to remember his wife, Jennifer Ouellette (https://cocktailpartyphysics.com/hello/) writes for a living. Who I was reading before she pointed me to Sean’s writing, back before she called him the Time Lord.
My favorite piece of her writing involves them both: Love Among the Equations (https://cocktailpartyphysics.com/love-among-the-equations/). Science writers seldom bring me to tears.
Something to consider. Space, by definition, is only 3 dimensions…it hence excludes Time. It therefore excludes Change (Time being the dimension referencing the objective fundament of Change…no Time = no Change).
So, without Time, Space is hence static.
Hi Sean,
“The derivative of the momentum is the acceleration, and the equation sets it equal to “the force divided by the mass,” just as Newton would have told you.”
The derivative of the momentum is the force, not the acceleration. 🙂 You get the acceleration when you divide the derivative of the momentum with the mass, and on the other side of the equation you then get force divided by mass. Which is what Newton says.
Just noting. And you may want to fix that sentence. 😉
Best, 🙂
Marko
Your stuff is baffling to me—but glorious, thank you!
Great post Sean, and happy thanksgiving!
At the moment I’m a bit sceptical about the usefulness of the Locality From the Spectrum paper. Whether or not a Hamiltonian looks k-local wrt some decomposition of Hilbert space seems to depend on the *precise* values of the spectrum. If we take a k-local Hamiltonian and perturb its eigenvalues slightly, it will almost always fail to stay k-local. But my gut feeling is that physics should depend continuously on values of parameters: we shouldn’t need to know the spectrum to infinite precision in order to make predictions.
Do you have any ideas about how the Locality From the Spectrum result might deal with this issue?
Thanks for all the great content – you’re a real inspiration to an aspiring physicist 🙂
It seems to me that there are three fundamental elements in the universe: spacetime, mass-energy, and motion. You can’t separate space and time; they came into existence together and are continuously being created in relation to each other. Nor can you separate mass and energy (which is why photons have momentum as well as particles). And in an expanding universe, nothing is stationary; everything is in motion. All three are captured in the Hamiltonian.
This Thanksgiving, we give thanks to Sean, who always gives us an interesting post on Thanksgiving.
vmarko is of course correct! I’ve fixed the post.
Sean,
You concluded the Thanksgiving message in part with:
“The answers are that most Hamiltonians aren’t compatible with locality in any sense, ….
Fine, but why that Hamiltonian? Who knows? This is above our pay grade right now, though it’s fun to speculate.”
One could speculate that quantum mechanics (QM) is by nature nonlocal. This is plainly evident in entanglement itself.
Even the term “nonlocal” stems from our classical values being imposed, unnaturally if you like, on QM.
That tradition actually started with Einstein, A., Podolsky, B. and Rosen, N., 1935, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”, Phys. Rev. 47, 777.
KC
Sean,
The type of approach adopted by Jordan Cotler, Geoffrey Penington, and Daniel Ranard is somewhat reminiscent of attempts (in general) to quantize classical space(time).
An alternative to address “why is there something called ‘space’ at all?”, consistent with your 2016 Thanksgiving message, is to simply note that the speed of light determines how far, in space, we could see. Rephrased, how much space are local to us.
One advantage of this approach is that in one fell swoop, both the space and the locality issues are jointly taken into consideration.
Possible applications of this approach are numerous. Take for example the “edge of the universe”. Does the universe have an edge? We don’t know. Now by using the speed of light, one could delimit the space inside the observable universe.
The question then becomes: Does the observable universe have an edge? Or, does something physically change at the edge of the observable universe? Again, we don’t know. But armed with a fixed speed of light, one could reason as follows.
When an observer moves to the edge of the observable universe, that edge becomes a new center. It is as if the observable universe has moved, over the distance of a radius, along with the observer. Viewed this way, nothing needs to physically change at the edge. But locality certainly moves with the observer.
Will briefly add causality and the expansion of the universe. Using light cone representation and world lines, causality is well depicted. So is locality. As such, if the edge of the observable universe is where things in space recede faster than light can reach back to us, we lose causal contact with them. Those things are also no longer local to us.
Will leave the implications of the above for now. Suffice it to note perhaps that when the worlds in Many-Worlds Interpretation are thought of as universes, it is easy to see why different worlds/universes are neither causal nor local to us.
KC
I’m just an amateur, but it seems like both the Newtonian, Hamiltonian and field-like descriptions given above and elsewhere assume a pre-existing set of positions, or coordinate frame. For instance:
“Newton…featured objects located in space, evolving with time. Each object has a trajectory, which is its position in space at each moment of time.”
‘Hamiltonian mechanics, where the fundamental variable isn’t “position,” but the combination of “position and momentum,”’
“field theory — space is suffused with fields, and what happens to a field at one point in space only directly depends on the other fields at precisely the same point in space”
I wonder if, instead, units of space/position are what is fundamental, and there’s only a coordinate system once there are more than one of these units. That is, they together form the coordinate system. And fields, energy and matter are just jiggling and/or relative movements of these units of space and location. The reason why interactions are local could be that a jiggling or moving unit will first interact with its neighboring units before this interaction can be transmitted to the other units. Time could just be a function of the number of changes these units go through. Maybe, these units could be called strings, membranes, loops or whatever? Just some speculations.
Overall, it seems like a pre-existing set of positions shouldn’t be assumed. Thanks.
Sean,
This year’s Thanksgiving message echoes your 2016 Atlantic Magazine article “All Physics Is Local” in concluding that quantum gravity will settle many questions, including those about locality and space.
Until we give thanks for quantum gravity come one November, on your question “why are
interactions local with respect to anything?” (“the question” in the remainder of this comment), Einstein’s spacetime based description works rather well to address locality.
As to why with respect to space, good question. Lacking an obvious answer provided by classical physics, one could try a quantum angle, in part to reflect the thinking that classical is emergent, likely from quantum.
In order to avoid redundancy, will refer to a comment which I made on June 2, 2019 in John Preskill’s blog “Quantum Information Meets Quantum Matter: Now Published!” (https://quantumfrontiers.com/2019/04/27/quantum-information-meets-quantum-matter-now-published/#comment-140051). It elaborated on a “Swiss cheese” model of the Universe.
Relevant to “the question”, the network of communicating “holes” in the block of cheese denotes communicating wormholes. If the equivalence between wormhole and entanglement is recognized, and classical cosmic structures are seen in the context of particles and quantum measurement (https://quantumfrontiers.com/2013/06/07/entanglement-wormholes/comment-page-2/#comment-82042), the interactions in “the question” are actually all non-local.
In short, by taking seriously the June comment, local interactions in space become non-local interactions in spacetime. That may seem like a sleight of hand. But as Robbert Dijkgraaf said in his “The End of Space and Time?” lecture: In quantum mechanics, anything you do fast enough is allowed.
Magic and tongue-in-cheek aside, have we answered “the question”? No, not using classical physics. But perhaps yes, in terms of quantum physics.
KC
Sean,
Other than being Dutch, there may be more to Dijkgraaf’s “Anything is allowed in quantum mechanics if you do it fast enough”.
Rephrased, “fast enough” can mean when it takes no time for something to occur. Or, time approaches zero. At an extreme, time drops out. Or, clocks run at the rate of zero.
(If time dropping out sounds familiar, that’s what happens with the Wheeler-DeWitt equation.)
In our universe served so well by spacetime, when time resigns, likely space is no longer an issue. In terms of speed of light that allowed Einstein to come up with spacetime, “zero space is traveled by a photon in zero second (clocks run at the rate zero)”.
One message could be: When thinking about quantum gravity, on the gravity side, we have spacetime. But on the quantum side, we may not (need to have either).
At the risk of overindulging (it’s Thanksgiving!), would point out that Einstein also told us what happens at a black hole: Clocks run at the rate zero.
KC
hmm
“Possible applications of this approach are numerous. Take for example the “edge of the universe”. Does the universe have an edge? We don’t know. Now by using the speed of light, one could delimit the space inside the observable universe.
The question then becomes: Does the observable universe have an edge? Or, does something physically change at the edge of the observable universe? Again, we don’t know. But armed with a fixed speed of light, one could reason as follows. ”
what if the observable universe were mobius shaped and within its nth cross section our milkyway exists in constant motion and what if we placed a rotating lighthouse in the middle of the unobservable donut hole of the mobius and assumed its flashing rate is at the speed of light. what would the implications be and what are the empirical constraints?
how malleable is a particle and its dimensionality?
onalimb,
Good questions about the observable universe, IF the universe is a mobius.
As for a particle’s malleability and dimensionality, in order not to stray afar, I would think one reasonable approach is to explore per accepted constraints laid down by the standard model of particles?
Best,
KC
“IF the universe is a mobius.”
that wasn’t the question. the question was what if the observable universe were mobius shaped?
it’s more of a thought experiment than a question. if one can not prove that the observable universe is not indeed mobius than your thought experiment :
https://quantumfrontiers.com/2018/11/25/theoretical-physics-has-not-gone-to-the-dogs/comment-page-1/#comment-117520
which you linked to in a reply to a comment on the Delayed Quantum Eraser post is, well, good, if the observable universe had edges and wasn’t mobius along with many assumptions. One needs to stray that far to posit such a thought experiment. so, it’s a bit contradictory to say:
“As for a particle’s malleability and dimensionality, in order not to stray afar, I would think one reasonable approach is to explore per accepted constraints laid down by the standard model of particles?” wouldn’t that be like holding a ruler up to the sky to measure the distance between the stars?
LGQ,
Thank you and onalimb for your interest in my thought experiment. Even though your questions arose from reading my September 21 comment in Sean’s “Notorious Delayed-Choice Quantum Eraser” blog, as they relate to the thought experiment, in part for housekeeping purposes, if you do not mind, will respond to you here as well.
Your “What empirical ways could this intangible switch be explained to reconcile the quantum & classical?” will be addressed in two parts.
The “intangible switch” refers to any measurement = entanglement = any interaction in the natural environment. As such, all three items, each by itself, need little explanation. As to why the three are grouped in this manner, I will be happy to elaborate if necessary.
As for “to reconcile the quantum & classical”, quantum reality is recognized to be the more fundamental reality (https://www.preposterousuniverse.com/blog/2018/01/17/beyond-falsifiability/comment-page-2/#comment-7295910552604315312), capable of giving rise to classical reality (https://www.preposterousuniverse.com/blog/2018/02/08/why-is-there-something-rather-than-nothing-2/comment-page-5/#comment-7295910552604315547).
And entanglement (aka measurement or natural interaction in the environment) is the mechanism mediating the emergence of classical reality. No claim is made that this reconciles quantum and classical. It is presented merely as one way for the two to work together.
Now to “What are the implications from the wave function evolving and what would that negate?”
That the wavefunction evolves is standard. The purpose is to account for all possible outcomes at measurement. What’s important to point out is that the wavefunction in this case is “nonphysical”, as required by the result of the thought experiment.
As such, there is no need to invoke a collapse (as in Copenhagen) or a splitting of worlds (as in Many-Worlds). Because there is nothing physical in the wavefunction to be disappeared by collapsing. Nor any physical worlds to split off, at measurement. Per unitarity, one measurement result is obtained. Or, one nonphysical quantum reality becomes physical reality. What happens to the rest? They remain nonphysical, awaiting the next measurement if you like.
In that sense, it negates (using your word) needing to have a Copenhagen vs. a Many-Worlds interpretation. It could potentially “unite” all interpretations by making all share a nonphysical wavefunction. That, by the way, also sidesteps whether the wavefundtion is ontic or epistemic.
A more complete description of how things work in a Universe with nonphysical quantum reality is available in a June 2, 2019 comment in John Preskill’s blog (https://quantumfrontiers.com/2019/04/27/quantum-information-meets-quantum-matter-now-published/#comment-140051).
Lastly, since the idea “real = physical” is so ingrained (https://quantumfrontiers.com/2019/01/27/humans-can-intuit-quantum-physics/comment-page-1/#comment-123863), lest a “nonphysical” quantum reality sounds unreal, will briefly describe the nature of a nonphysical quantum field.
If a physical particle is the result of local excitation of a nonphysical quantum field, before that particle is observed, the underlying quantum field is indifferent. In other words, what a given nonphysical quantum field manifests (at measurement), depends on the “tool” involved.
To illustrate, a stationary observer, one that is accelerating, a black hole, or two closely placed parallel plates, would yield, in the order of the tools listed, a particle, Unruh radiation, Hawking radiation and quantum fluctuations seen in the Casimir effect, all from the same nonphysical quantum field.
The above was touched on in Sean’s Gifford Lectures blog posted on November 23, 2016 (https://www.preposterousuniverse.com/blog/2016/11/23/gifford-lectures-on-natural-theology/#comment-7295910552604313840).
Incidentally, all four “tools” mentioned above are means to effect that “intangible switch” mentioned at the beginning of this reply.
Had your questions been misinterpreted, and to the extent this reply partially overlaps my comment on November 18, 2019 (https://www.preposterousuniverse.com/blog/2019/09/21/the-notorious-delayed-choice-quantum-eraser/#comment-7295910552604316840), my apologies.
Best,
KC
Thanks for taking the time to respond, Lee. Though your Dec 17 6:30 AM comment along with my reply regarding TQFT being reason behind the interest in knowing about the degree of malleability of a particle and its dimensionality are excluded, hopefully the sequence of logic is still intact.
“The ‘intangible switch’….. to work together.”
Yes, so basically following this representation and the four tools you mentioned that are means to effect the intangible switch, simply put, knowledge of topological properties might give rise to tools of similar effect. To represent it more obviously as a tool, think of the ‘intangible switch’, which could be rooted in the topology of particles and dimensionality, as Vieta jumping between quantum and classical.