Energy Conservation and Non-Conservation in Quantum Mechanics

Conservation of energy is a somewhat sacred principle in physics, though it can be tricky in certain circumstances, such as an expanding universe. Quantum mechanics is another context in which energy conservation is a subtle thing — so much so that it’s still worth writing papers about, which Jackie Lodman and I recently did. In this blog post I’d like to explain two things:

• In the Many-Worlds formulation of quantum mechanics, the energy of the wave function of the universe is perfectly conserved. It doesn’t “require energy to make new universes,” so that is not a respectable objection to Many-Worlds.
• In any formulation of quantum mechanics, energy doesn’t appear to be conserved as seen by actual observers performing quantum measurements. This is a not-very-hard-to-see aspect of quantum mechanics, which nevertheless hasn’t received a great deal of attention in the literature. It is a phenomenon that should be experimentally observable, although as far as I know it hasn’t yet been; we propose a simple experiment to do so.

The first point here is well-accepted and completely obvious to anyone who understands Many-Worlds. The second is much less well-known, and it’s what Jackie and I wrote about. I’m going to try to make this post accessible to folks who don’t know QM, but sometimes it’s hard to make sense without letting the math be the math.

First let’s think about energy in classical mechanics. You have a system characterized by some quantities like position, momentum, angular momentum, and so on, for each moving part within the system. Given some facts of the external environment (like the presence of gravitational or electric fields), the energy is simply a function of these quantities. You have for example kinetic energy, which depends on the momentum (or equivalently on the velocity), potential energy, which depends on the location of the object, and so on. The total energy is just the sum of all these contributions. If we don’t explicitly put any energy into the system or take any out, the energy should be conserved — i.e. the total energy remains constant over time.

There are two main things you need to know about quantum mechanics. First, the state of a quantum system is no longer specified by things like “position” or “momentum” or “spin.” Those classical notions are now thought of as possible measurement outcomes, not well-defined characteristics of the system. The quantum state — or wave function — is a superposition of various possible measurement outcomes, where “superposition” is a fancy term for “linear combination.”

Consider a spinning particle. By doing experiments to measure its spin along a certain axis, we discover that we only ever get two possible outcomes, which we might call “spin-up” or “” and “spin-down” or “.” But before we’ve made the measurement, the system can be in some superposition of both possibilities. We would write , the wave function of the spin, as

   

where and are numerical coefficients, the “amplitudes” corresponding to spin-up and spin-down, respectively. (They will generally be complex numbers, but we don’t have to worry about that.)

The second thing you have to know about quantum mechanics is that measuring the system changes its wave function. When we have a spin in a superposition of this type, we can’t predict with certainty what outcome we will see. All we can predict is the probability, which is given by the amplitude squared. And once that measurement is made, the wave function “collapses” into a state that is purely what is observed. So we have

   

At least, that’s what we teach our students — Many-Worlds has a slightly more careful story to tell, as we’ll see.

We can now ask about energy, but the concept of energy in quantum mechanics is a bit different from what we are used to in classical mechanics. Classically, a single particle has a constant energy, given by the sum of its potential energy (which depends on its position) and its kinetic energy (which depends on its momentum). But in quantum mechanics, the state of the particle isn’t specified by position and velocity; those are just possible measurement outcomes. The state of the system is given by the wave function.

There are, however, special states called eigenstates, in which some particular observable has a definite value. So we have “position eigenstates,” for which the position is exactly defined, “momentum eigenstates,” for which momentum is exactly defined, and so on. There are no states for which both position and momentum are exactly defined — that would violate the Heisenberg uncertainty principle. And indeed, in most states neither one of them is exactly defined. But we can think of any state as a superposition of position eigenstates, or as a superposition of momentum eigenstates (but not both).

The same goes for energy, which is an observable quantity just like position or momentum. There are energy eigenstates, where the energy has a definite value, but neither position nor momentum do. And if you happen to be in an energy eigenstate, “energy conservation” is trivially true — the energy stays the same. But that’s a much less interesting statement than in classical mechanics, because energy eigenstates don’t evolve at all! A system with a definite energy just sits there, stationary and unevolving.

Fortunately, most states don’t have a definite energy, but rather are superpositions of different energy eigenstates. That’s good, because the system as a whole can then evolve. All the interesting evolution of quantum systems can actually be thought of as different energy eigenstates combining to give time-dependent answers to questions we could ask about other quantities like position or momentum.

But what can we say about energy conservation if a quantum state doesn’t even have a definite energy? Well, we can still associate an average energy to any particular quantum state, even if specific measurements might give answers that fluctuate around that central value. (For experts: the expectation value of the Hamiltonian.) If we think of an arbitrary quantum state as a weighted superposition of various specific-energy eigenstates, the average energy is just what it sounds like: the weighted average of the energies of all those eigenstates.

Let’s imagine that we’re in the state described above, a superposition of spin-up and spin-down. And let’s further imagine that the spin-up state is a state with definite energy (i.e. it’s an energy eigenstate) , and the spin-down state has a definite energy . Then the average energy is just a combination of both these values, weighted by the squares of the amplitudes:

   

As long as the quantum system obeys the Schrödinger equation, you will be happy to hear that the average energy is precisely conserved. It doesn’t change over time. That’s the notion of “energy conservation” you have in quantum mechanics: the average or expected value stays constant, as long as you obey the Schrödinger equation.

Alas, there is a famous case in which quantum systems do not obey the Schrödinger equation, or at least they appear not to: when they are being measured. As we said above, what we teach our students is that wave functions collapse when they are observed; this collapse process is unpredictable, and doesn’t obey the Schrödinger equation. As a result, the average energy is not conserved in the process of quantum measurement. Indeed, as we can quickly see by comparing with the equations we started with, after we do the measurement the system will either have energy (if we measured spin-up) or it will have energy (if we measured spin-down). And in general, if those two values are unequal (and both and are non-zero), neither one of those will be the same as our original average .

This is all pretty straightforward, almost trivial! And indeed, I wouldn’t object if you thought that. But people like energy conservation, deep in their bones. So what I suspect is that, if you asked most working quantum physicists what was going on here, they would guess that the total energy of the universe actually is conserved, but you just weren’t keeping track of it accurately. After all, there needs to be some apparatus and observer who interact with the system in order to measure it. Perhaps whenever the energy changes in the system we observe, there is a compensating change in energy in the apparatus or the rest of the world, so that the total is conserved.

Not so, or at least not in quantum mechanics as we generally understand it. That’s what we show in the paper Jackie and I recently submitted.

Energy Non-Conservation in Quantum Mechanics

Sean M. Carroll and Jackie Lodman

We study the conservation of energy, or lack thereof, when measurements are performed in quantum mechanics. The expectation value of the Hamiltonian of a system can clearly change when wave functions collapse in accordance with the standard textbook (Copenhagen) treatment of quantum measurement, but one might imagine that the change in energy is compensated by the measuring apparatus or environment. We show that this is not true; the change in the energy of a state after measurement can be arbitrarily large, independent of the physical measurement process. In Everettian quantum theory, while the expectation value of the Hamiltonian is conserved for the wave function of the universe (including all the branches), it is not constant within individual worlds. It should therefore be possible to experimentally measure violations of conservation of energy, and we suggest an experimental protocol for doing so.

Basically what we do is to construct a complete toy model of both a system and a measuring apparatus, one sufficiently simple that we can keep track of the energy exactly. And we verify that the change in energy of the system has no necessary connection at all to the change in energy of the rest of the world. (As we explain in the paper, other people have pointed to this phenomenon before, but usually in the context of trying to avoid it; we are more celebratory, and suggest that people should be looking for this experimentally.)

So, if you’re a textbook/Copenhagen kind of person, the punchline is simple: energy is not conserved in quantum measurements. Really the only way out is to refuse to accept the “average energy” of a state as representing the true energy at all. That’s fine, as far as it goes. But in that case almost no states (i.e., no states other than energy eigenstates) will have a well-defined energy. And as we say in the paper, the average energy is a rigorous energy-like quantity that would be perfectly conserved if it weren’t for measurements. So the fact that measurements violate that conservation law is pretty interesting.

Now we can come to the Everettian perspective, which puts a very attractive spin on things. I won’t go too deeply into the Everettian formulation itself; see this delightful book, or this somewhat shorter blog post. The point is that in Everett, wave functions never collapse; all they ever do is obey the Schrödinger equation. What you and I think of as a “measurement” is just when a quantum system in a superposition becomes entangled with some macroscopic object (the “measuring apparatus”), which in turn becomes entangled with its environment (“decoherence”). When that happens, the different parts of the superposition become parts of separate worlds. So rather than our above superposition of spin-up and spin-down suddenly collapsing into one or the other, the state evolves smoothly into one describing two non-interacting copies of reality, one where the spin is up and the other where the spin is down.

The nice thing about this is: energy is completely conserved! Individual observers think that they witness the average energy changing, because they only live in one branch at a time. But in the “wave function of the universe” (the quantum state describing all branches at once), the average energy is a constant, since that wave function obeys the Schrödinger equation. The energy simply gets divided up between branches slightly differently as time goes on.

This story is very different than what you might often hear, namely that it’s Everett, not Copenhagen, that has a problem with energy conservation. After all, where does the energy come from to make all those worlds?

Hopefully this worry has been completely dissipated by the discussion above. The point is that there are two different senses of the word “energy”: the energy that observers within any branch (world) might attribute to the reality they see, and the total energy of all the branches combined. If a wave function describes a collection of many branches labeled , with amplitudes and average energies , the average energy of the whole shebang is

   

So even though there are more and more branches as time evolves, the contribution of each branch to the total energy is weighted by the factors , and those numbers go down over time as branches split. The effects precisely cancel, so that the total energy of the universe (all branches included) is constant. It’s just that individual branches get “thinner” over time (their amplitudes get smaller), so they make smaller and smaller contributions to the total.

This “thinning” process is completely invisible from inside. You have no way of knowing what the amplitude of your particular branch is; it’s invisible to you. The fact that the amplitudes go down doesn’t mean that the world around you looks somehow less tangible or energetic. The energy you would calculate by adding up the individual energies of all the stuff in the universe (stars, planets, black holes, dark matter, etc) goes into the energy of your particular branch; there’s no reason for that number to systematically diminish over time. (Given the tiny changes in average energy that can happen at measurement events, the energy of your world as seen from inside will undergo a gradual random walk of gradually-diminishing steps, but honestly the changes are so incredibly tiny that you’d never notice.)

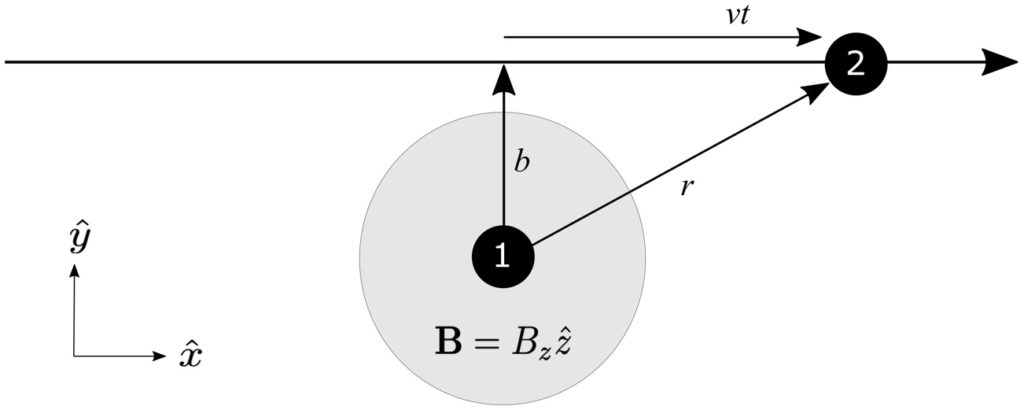
Is this change of the average energy of the universe (as seen by observers on individual branches) potentially observable in experiments? In principle, absolutely yes; in practice, maybe, but it would be hard. Not particle-accelerator-the-size-of-the-galaxy hard, but a challenge. This is the other thing that Jackie and I suggest in our paper. The trick is that (1) it’s extremely hard in practice to construct superpositions of very different energy states, so any hoped-for changes in average energy will be very tiny; and (2) any measurement generally spills a lot of energy all over the place, which is hard to keep track of. I won’t go into details, but we suggest a general protocol, and also a specific implementation where one spinning particle is kept stationary in a trap, while another travels by it and they become entangled. Then by measuring the spin of the moving particle, we can change the spin of the stationary one, hopefully changing its energy in the process.

I’m honestly not sure how feasible this kind of experiment is; that’s above my pay grade. But it’s a nice example of how thinking carefully about the foundations of quantum mechanics can lead to interesting ideas.