Note: It is in the nature of book-writing that sometimes you write things that don’t end up appearing in the final book. I had a few such examples for Something Deeply Hidden, my book on quantum mechanics, Many-Worlds, and emergent spacetime. Most were small and nobody will really miss them, but I did feel bad about eliminating my discussion of the “delayed-choice quantum eraser,” an experiment that has caused no end of confusion. So here it is, presented in full. It’s a bit too technical for the book, I don’t know what I was thinking!
Let’s imagine you’re an undergraduate physics student, taking an experimental lab course, and your professor is in a particularly ornery mood. So she forces you to do a weird version of the double-slit experiment, explaining that this is something called the “delayed-choice quantum eraser.” You think you remember seeing a YouTube video about this once.
In the conventional double-slit, we send a beam of electrons through two slits and on toward a detecting screen. Each individual electron hits the screen and leaves a dot, but if we build up many such detections, we see an interference pattern of light and dark bands, because the wave function passing through the two slits interferes with itself. But if we also measure which slit each electron goes through, the interference pattern disappears, and we see a smoothed-out distribution at the screen. According to textbook quantum mechanics that’s because the wave function collapsed when we measured it at the slits; according to Many-Worlds it’s because the electron became entangled with the measurement apparatus, decoherence occurred as the apparatus became entangled with the environment, and the wave function branched into separate worlds, in each of which the electron only passes through one of the slits.
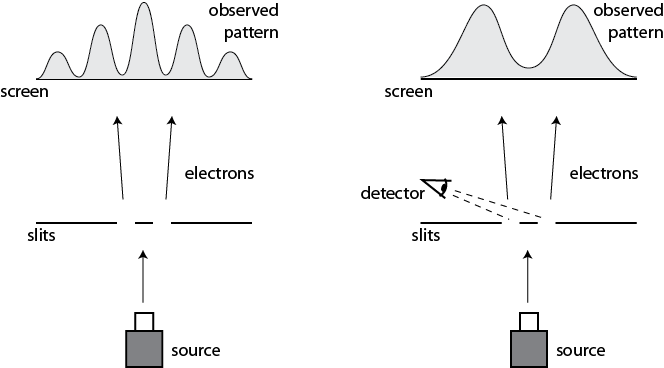
unless a detector measures which slit each electron goes through (right).
The new wrinkle is that we are still going to “measure” which slit the electron goes through, but instead of reading it out on a big macroscopic dial, we simply store that information in a single qubit. Say that for every “traveling” electron passing through the slits, we have a separate “recording” electron. The pair becomes entangled in the following way: if the traveling electron goes through the left slit, the recording electron is in a spin-up state (with respect to the vertical axis), and if the traveling electron goes through the right, the recording electron is spin-down. We end up with:
Ψ= (L)[↑] + (R)[↓].
Our professor, who is clearly in a bad mood, insists that we don’t actually measure the spin of our recording electrons, and we don’t even let them wander off and bump into other things in the room. We carefully trap them and preserve them, perhaps in a magnetic field.
What do we see at the screen when we do this with many electrons? A smoothed-out distribution with no interference pattern, of course. Interference can only happen when two things contribute to exactly the same wave function, and since the two paths for the traveling electrons are now entangled with the recording electrons, the left and right paths are distinguishable, so we don’t see any interference pattern. In this case it doesn’t matter that we didn’t have honest decoherence; it just matters that the traveling electrons were entangled with the recording electrons. Entanglement of any sort kills interference.
Of course, we could measure the recording spin if we wanted to. If we measure it along the vertical axis, we will see either [↑] or [↓]. Referring back to the quantum state Ψ above, we see that this will put us in either a universe where the traveling electron went through the left slit, or one where it went through the right slit. At the end of the day, recording the positions of many such electrons when they hit the detection screen, we won’t see any interference.
Okay, says our somewhat sadistic professor, rubbing her hands together with villainous glee. Now let’s measure all of our recording spins, but this time measure them along the horizontal axis instead of the vertical one. As we saw in Chapter Four, there’s a relationship between the horizontal and vertical spin states; we can write
[↑] = [→] + [←] ,
[↓] = [→] – [←].
(To keep our notation simple we’re ignoring various factors of the square root of two.) So the state before we do such a measurement is
Ψ = (L)[→] + (L)[←] + (R)[→] – (R)[←]
= (L + R)[→] + (L – R)[←].
When we measured the recording spin in the vertical direction, the result we obtained was entangled with a definite path for the traveling electron: [↑] was entangled with (L), and [↓] was entangled with (R). So by performing that measurement, we knew that the electron had traveled through one slit or the other. But now when we measure the recording spin along the horizontal axis, that’s no longer true. After we do each measurement, we are again in a branch of the wave function where the traveling electron passes through both slits. If we measured spin-left, the traveling electron passing through the right slit picks up a minus sign in its contribution to the wave function, but that’s just math.
By choosing to do our measurement in this way, we have erased the information about which slit the electron went through. This is therefore known as a “quantum eraser experiment.” This erasure doesn’t affect the overall distribution of flashes on the detector screen. It remains smooth and interference-free.
But we not only have the overall distribution of electrons hitting the detector screen; for each impact we know whether the recording electron was measured as spin-left or spin- right. So, instructs our professor with a flourish, let’s go to our computers and separate the flashes on the detector screen into these two groups — those that are associated with spin- left recording electrons, and those that are associated with spin-right. What do we see now?
Interestingly, the interference pattern reappears. The traveling electrons associated with spin-left recording electrons form an interference pattern, as do the ones associated with spin-right. (Remember that we don’t see the pattern all at once, it appears gradually as we detect many individual flashes.) But the two interference patterns are slightly shifted from each other, so that the peaks in one match up with the valleys in the other. There was secretly interference hidden in what initially looked like a featureless smudge.
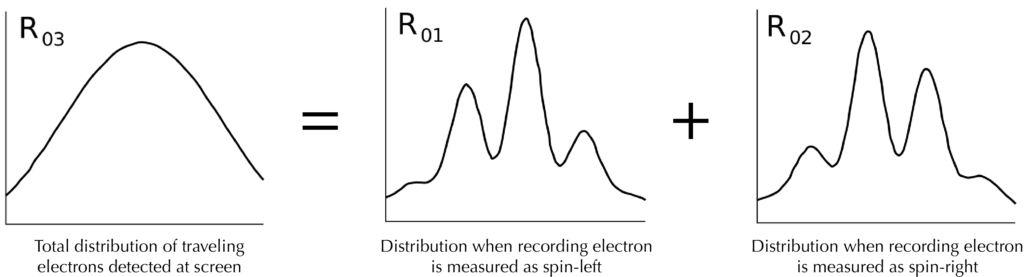
In retrospect this isn’t that surprising. From looking at how our quantum state Ψ was written with respect to the spin-left and -right recording electrons, each measurement was entangled with a traveling electron going through both slits, so of course it could interfere. And that innocent-seeming minus sign shifted one of the patterns just a bit, so that when combined together the two patterns could add up to a smooth distribution.
You professor seems more amazed by this than you are. “Don’t you see,” she exclaims excitedly. “If we didn’t measure the recording photons at all, or if we measured them along the vertical axis, there was no interference anywhere. But if we measured them along the horizontal axis, there secretly was interference, which we could discover by separating out what happens at the screen when the recording spin was left or right.”
You and your classmates nod their heads, cautiously but with some degree of confusion.
“Think about what that means! The choice about whether to measure our recording spins vertically or horizontally could have been made long after the traveling photons splashed on the recording screen. As long as we stored our recording spins carefully and protected them from becoming entangled with the environment, we could have delayed that choice until years later.”
Sure, the class mumbles to themselves. That sounds right.
“But interference only happens when the traveling electron goes through both slits, and the smooth distribution happens when it goes through only one slit. That decision — go through both slits, or just through one — happens long before we measure the recording electrons! So obviously, our choice to measure them horizontally rather than vertically had to send a signal backward in time to tell the traveling electrons to go through both slits rather than just one!”
After a short, befuddled pause, the class erupts with objections. Decisions? Backwards in time? What are we talking about? The electron doesn’t make a choice to travel through one slit or the other. Its wave function (and that of whatever it’s entangled with) evolves according to the Schrödinger equation, just like always. The electron doesn’t make choices, it unambiguously goes through both slits, but it becomes entangled along the way. By measuring the recording photons along different directions, we can pick out different parts of that entangled wave function, some of which exhibit interference and others do not. Nothing really went backwards in time. It’s kind of a cool result, but it’s not like we’re building a frickin’ time machine here.
You and your classmates are right. Your instructor has gotten a little carried away. There’s a temptation, reinforced by the Copenhagen interpretation, to think of an electron as something “with both wave-like and particle-like properties.” If we give into that temptation, it’s a short journey to thinking that the electron must behave in either a wave- like way or a particle-like way when it passes through the slits, and in any given experiment it will be one or the other. And from there, the delayed-choice experiment does indeed tend to suggest that information had to go backwards in time to help the electron make its decision. And, to be honest, there is a tradition in popular treatments of quantum mechanics to make things seem as mysterious as possible. Suggesting that time travel might be involved somehow is just throwing gasoline on the fire.
All of these temptations should be resisted. The electron is simply part of the wave function of the universe. It doesn’t make choices about whether to be wave-like or particle-like. But a number of serious researchers in quantum foundations really do take the delayed-choice quantum eraser and analogous experiments (which have been successfully performed, by the way) as evidence of retrocausality in nature — signals traveling backwards in time to influence the past. A form of this experiment was originally proposed by none other than John Wheeler, who envisioned a set of telescopes placed on the opposite side of the screen from the slits, which could detect which slit the electrons went through long after they had passed through. Unlike some later commentators, Wheeler didn’t go so far as to suggest retrocausality, and knew better than to insist that an electron is either a particle or a wave at all times.
There’s no need to invoke retrocausality to explain the delayed-choice experiment. To an Everettian, the result makes perfect sense without anything traveling backwards in time. The trickiness relies on the fact that by becoming entangled with a single recording spin rather than with the environment and its zillions of particles, the traveling electrons only became kind-of decohered. With just a single particle to worry about observing, we are allowed to contemplate measuring it in different ways. If, as in the conventional double- slit setup, we measured the slit through which the traveling electron went via a macroscopic pointing device, we would have had no choice about what was being observed. True decoherence takes a tiny quantum entanglement and amplifies it, effectively irreversibly, into the environment. In that sense the delayed-choice quantum eraser is a useful thought experiment to contemplate the role of decoherence and the environment in measurement.
But alas, not everyone is an Everettian. In some other versions of quantum mechanics, wave functions really do collapse, not just the apparent collapse that decoherence provides us with in Many-Worlds. In a true collapse theory like GRW, the process of wave- function collapse is asymmetric in time; wave functions collapse, but they don’t un- collapse. If you have collapsing wave functions, but for some reason also want to maintain an overall time-symmetry to the fundamental laws of physics, you can convince yourself that retrocausality needs to be part of the story.
Or you can accept the smooth evolution of the wave function, with branching rather than collapses, and maintain time-symmetry of the underlying equations without requiring backwards-propagating signals or electrons that can’t make up their mind.
We don’t observe the electrons passing through the slits, but observe the experiment from a distance. We see what appears to be a person observing the slit. Unknown to us, it was just a cardboard cutout, which is later removed while our attention is elsewhere. Still later, we go and observe the pattern of the electrons. Do we see interference or not?