Sir Michael Atiyah, one of the world’s greatest living mathematicians, has proposed a derivation of α, the fine-structure constant of quantum electrodynamics. A preprint is here. The math here is not my forte, but from the theoretical-physics point of view, this seems misguided to me.
(He’s also proposed a proof of the Riemann conjecture, I have zero insight to give there.)
Caveat: Michael Atiyah is a smart cookie and has accomplished way more than I ever will. It’s certainly possible that, despite the considerations I mention here, he’s somehow onto something, and if so I’ll join in the general celebration. But I honestly think what I’m saying here is on the right track.
In quantum electrodynamics (QED), α tells us the strength of the electromagnetic interaction. Numerically it’s approximately 1/137. If it were larger, electromagnetism would be stronger, atoms would be smaller, etc; and inversely if it were smaller. It’s the number that tells us the overall strength of QED interactions between electrons and photons, as calculated by diagrams like these.
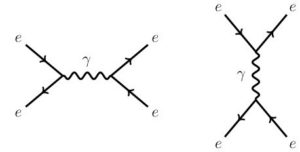As Atiyah notes, in some sense α is a fundamental dimensionless numerical quantity like e or π. As such it is tempting to try to “derive” its value from some deeper principles. Arthur Eddington famously tried to derive exactly 1/137, but failed; Atiyah cites him approvingly.
But to a modern physicist, this seems like a misguided quest. First, because renormalization theory teaches us that α isn’t really a number at all; it’s a function. In particular, it’s a function of the total amount of momentum involved in the interaction you are considering. Essentially, the strength of electromagnetism is slightly different for processes happening at different energies. Atiyah isn’t even trying to derive a function, just a number.
This is basically the objection given by Sabine Hossenfelder. But to be as charitable as possible, I don’t think it’s absolutely a knock-down objection. There is a limit we can take as the momentum goes to zero, at which point α is a single number. Atiyah mentions nothing about this, which should give us skepticism that he’s on the right track, but it’s conceivable.
More importantly, I think, is the fact that α isn’t really fundamental at all. The Feynman diagrams we drew above are the simple ones, but to any given process there are also much more complicated ones, e.g.
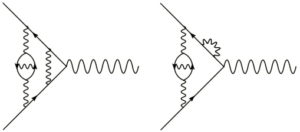And in fact, the total answer we get depends not only on the properties of electrons and photons, but on all of the other particles that could appear as virtual particles in these complicated diagrams. So what you and I measure as the fine-structure constant actually depends on things like the mass of the top quark and the coupling of the Higgs boson. Again, nowhere to be found in Atiyah’s paper.
Most importantly, in my mind, is that not only is α not fundamental, QED itself is not fundamental. It’s possible that the strong, weak, and electromagnetic forces are combined into some Grand Unified theory, but we honestly don’t know at this point. However, we do know, thanks to Weinberg and Salam, that the weak and electromagnetic forces are unified into the electroweak theory. In QED, α is related to the “elementary electric charge” e by the simple formula α = e2/4π. (I’ve set annoying things like Planck’s constant and the speed of light equal to one. And note that this e has nothing to do with the base of natural logarithms, e = 2.71828.) So if you’re “deriving” α, you’re really deriving e.
But e is absolutely not fundamental. In the electroweak theory, we have two coupling constants, g and g’ (for “weak isospin” and “weak hypercharge,” if you must know). There is also a “weak mixing angle” or “Weinberg angle” θW relating how the original gauge bosons get projected onto the photon and W/Z bosons after spontaneous symmetry breaking. In terms of these, we have a formula for the elementary electric charge: e = g sinθW. The elementary electric charge isn’t one of the basic ingredients of nature; it’s just something we observe fairly directly at low energies, after a bunch of complicated stuff happens at higher energies.
Not a whit of this appears in Atiyah’s paper. Indeed, as far as I can tell, there’s nothing in there about electromagnetism or QED; it just seems to be a way to calculate a number that is close enough to the measured value of α that he could plausibly claim it’s exactly right. (Though skepticism has been raised by people trying to reproduce his numerical result.) I couldn’t see any physical motivation for the fine-structure constant to have this particular value
These are not arguments why Atiyah’s particular derivation is wrong; they’re arguments why no such derivation should ever be possible. α isn’t the kind of thing for which we should expect to be able to derive a fundamental formula, it’s a messy low-energy manifestation of a lot of complicated inputs. It would be like trying to derive a fundamental formula for the average temperature in Los Angeles.
Again, I could be wrong about this. It’s possible that, despite all the reasons why we should expect α to be a messy combination of many different inputs, some mathematically elegant formula is secretly behind it all. But knowing what we know now, I wouldn’t bet on it.
Sorry for being off topic, but since you will in a few hours be on the Weekly Space Hangout of Fraser Cain, I have a question that might entertain the more general public there.
These five minutes in the video clip below explaining the essence of the mystery of quantum mechanics in terms of playing “20 questions” is fun. The point being that there is no right answer to begin with, but that the only important thing is that all the answers agree logically with one another. So the outcome depends on what questions are being asked, and that this is our “reality”. (Isn’t that how philosophers work, btw?):
https://youtu.be/q7v5NtV8v6I?t=2028
I also want to ask the hardest of all questions in philosophy. Is there in modern physics any (possible) refutation of solipsism, the idea that there is nothing “out there” but that it is all just a dream in my magic mind?
“If we had a more precise measurement of the fine structure constant, then we could compare Atiyah’s predicted number to the actual one.
How hard would it be to add more decimal points to our measurement of this constant?”
Pretty hard. But it is also important to add more decimal places to the traditional calculation, which is also pretty hard.
“Thank you, Sean, for calling bullshit on Atiyah’s claim.”
Probably the most polite bullshit claim ever! 😐
A famous paper by Beck, Bethe, and Riezler, recounted in “A Random Walk in Science” (1973), derived the fine structure constant thus:
This paper is a classic, the original reverse Sokal hoax, decades before the Bogdanov affair.
The original is in German. Fortunately, the point is not lost in translation.
I don’t think that it shows the editors’ sense of humour, though; I believe that they were duped.
While I share the general skepticism that warrants such a claim I wanted to give Atiyah the benefit of doubt and checked his own formulas to calculate the inverse of the fine-structure constant, using only his equations (1.1) and (7.1), both if which are elementary. I find that the value of 1/alpha following from these two equations is 0.16026… (which is very far from 137.035999…) so I am very confused about the main claim.
If anyone wants to cross-check, performing the infinite sum I get for the right hand side of (7.1) an exact expression in terms of first derivatives of PolyLogs w.r.t. to the first argument, which numerically evaluates to 0.05889. Explicitly, the r.h.s. of (7.1) yields (2+PolyLog'[1,1/2]+PolyLog'[-1,1/2])/ln[2], where PolyLog'[n,z] := (d/dk PolyLog[k,z])_{k\to n}.
I also disagree with the claim below (7.1) that the bounded sequence is monotonically increasing – it is not, at least for the usual interpretation of the symbols in (7.1).
If anyone has a comment or correction on this then please let me know. Note again that I made no attempt to check why (1.1) or (7.1) should be true in the first place – I merely checked that their combination does not give the right value of the fine structure constant.
Likely the Atiyah paper is not going to stand up to scrutiny. I also didn’t try to figure out all the math, but I don’t think I would argue against it with “its a function not a limit” or “its not fundamental” or “it doesn’t consider all the complex physics involved”. If he is right, his contribution will be along the line of Rydberg proposing a formula that worked, but had an undetermined constant later derived by Bohr with an oversimplified model and then later the full expression was derived from quantum theory. He is proposing an algorithm that should be able to predict more decimal places than are currently known. He claims he currently reproduces 9. If the method gives the remaining known digit that would be promising. Then if it correctly predicts presently unknown digits the way Rydberg’s formula predicted unknown lines, we’ll have a formula without a derivation. Likely it won’t pan out, but I don’t think it is clear thinking to argue it is misguided for not being a derivation when it only makes sense as a proposed formula.
I’m quite old, retired and old. But I had my Ph.D. in Theoretical Particle Physics in 1981 (since then I worked in IT).
At that time I worked on renormalization of QED and , more generally, of the Yang-Mill theories.
Your arguments are more sound to me than those of Atiyah.