Everyone is rightly excited about the latest gravitational-wave discovery. The LIGO observatory, recently joined by its European partner VIRGO, had previously seen gravitational waves from coalescing black holes. Which is super-awesome, but also a bit lonely — black holes are black, so we detect the gravitational waves and little else. Since our current gravitational-wave observatories aren’t very good at pinpointing source locations on the sky, we’ve been completely unable to say which galaxy, for example, the events originated in.
This has changed now, as we’ve launched the era of “multi-messenger astronomy,” detecting both gravitational and electromagnetic radiation from a single source. The event was the merger of two neutron stars, rather than black holes, and all that matter coming together in a giant conflagration lit up the sky in a large number of wavelengths simultaneously.
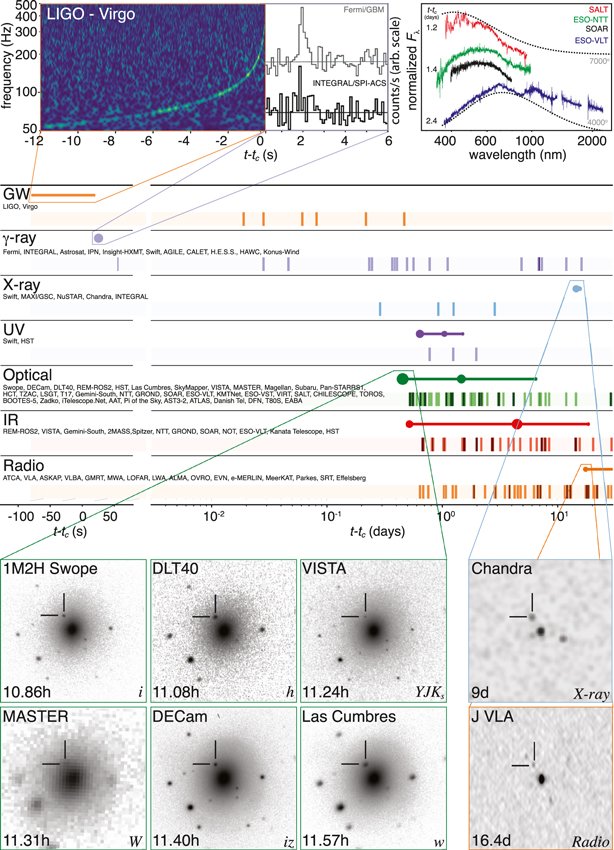 Look at all those different observatories, and all those wavelengths of electromagnetic radiation! Radio, infrared, optical, ultraviolet, X-ray, and gamma-ray — soup to nuts, astronomically speaking.
Look at all those different observatories, and all those wavelengths of electromagnetic radiation! Radio, infrared, optical, ultraviolet, X-ray, and gamma-ray — soup to nuts, astronomically speaking.
A lot of cutting-edge science will come out of this, see e.g. this main science paper. Apparently some folks are very excited by the fact that the event produced an amount of gold equal to several times the mass of the Earth. But it’s my blog, so let me highlight the aspect of personal relevance to me: using “standard sirens” to measure the expansion of the universe.
We’re already pretty good at measuring the expansion of the universe, using something called the cosmic distance ladder. You build up distance measures step by step, determining the distance to nearby stars, then to more distant clusters, and so forth. Works well, but of course is subject to accumulated errors along the way. This new kind of gravitational-wave observation is something else entirely, allowing us to completely jump over the distance ladder and obtain an independent measurement of the distance to cosmological objects. See this LIGO explainer.
The simultaneous observation of gravitational and electromagnetic waves is crucial to this idea. You’re trying to compare two things: the distance to an object, and the apparent velocity with which it is moving away from us. Usually velocity is the easy part: you measure the redshift of light, which is easy to do when you have an electromagnetic spectrum of an object. But with gravitational waves alone, you can’t do it — there isn’t enough structure in the spectrum to measure a redshift. That’s why the exploding neutron stars were so crucial; in this event, GW170817, we can for the first time determine the precise redshift of a distant gravitational-wave source.
Measuring the distance is the tricky part, and this is where gravitational waves offer a new technique. The favorite conventional strategy is to identify “standard candles” — objects for which you have a reason to believe you know their intrinsic brightness, so that by comparing to the brightness you actually observe you can figure out the distance. To discover the acceleration of the universe, for example, astronomers used Type Ia supernovae as standard candles.
Gravitational waves don’t quite give you standard candles; every one will generally have a different intrinsic gravitational “luminosity” (the amount of energy emitted). But by looking at the precise way in which the source evolves — the characteristic “chirp” waveform in gravitational waves as the two objects rapidly spiral together — we can work out precisely what that total luminosity actually is. Here’s the chirp for GW170817, compared to the other sources we’ve discovered — much more data, almost a full minute!
So we have both distance and redshift, without using the conventional distance ladder at all! This is important for all sorts of reasons. An independent way of getting at cosmic distances will allow us to measure properties of the dark energy, for example. You might also have heard that there is a discrepancy between different ways of measuring the Hubble constant, which either means someone is making a tiny mistake or there is something dramatically wrong with the way we think about the universe. Having an independent check will be crucial in sorting this out. Just from this one event, we are able to say that the Hubble constant is 70 kilometers per second per megaparsec, albeit with large error bars (+12, -8 km/s/Mpc). That will get much better as we collect more events.
So here is my (infinitesimally tiny) role in this exciting story. The idea of using gravitational-wave sources as standard sirens was put forward by Bernard Schutz all the way back in 1986. But it’s been developed substantially since then, especially by my friends Daniel Holz and Scott Hughes. Years ago Daniel told me about the idea, as he and Scott were writing one of the early papers. My immediate response was “Well, you have to call these things `standard sirens.'” And so a useful label was born.
Sadly for my share of the glory, my Caltech colleague Sterl Phinney also suggested the name simultaneously, as the acknowledgments to the paper testify. That’s okay; when one’s contribution is this extremely small, sharing it doesn’t seem so bad.
By contrast, the glory attaching to the physicists and astronomers who pulled off this observation, and the many others who have contributed to the theoretical understanding behind it, is substantial indeed. Congratulations to all of the hard-working people who have truly opened a new window on how we look at our universe.
Frances– I think the general areas are just “general relativity” and “theoretical astrophysics.” These are both big areas, especially the latter, but there’s an enormous amount of research involved in these kinds of discoveries, and it’s all helpful — stellar structure, nucleosynthesis, radiative transfer, particle physics, plasma physics, cosmology, etc.
This has changed now, as we’ve launched the era of “multi-messenger astronomy,”…
[Small sigh…]
In some respects, “multi-messenger astronomy” dates to the 1950s/1960s, with the direct detection of particles from the solar wind (various Soviet satellites), and then with the detection of solar neutrinos in the mid-1960s.
Even if you want to exclude the Sun from “astronomy” as some sort of special case, multi-messenger astronomy certainly dates to the late 1980s. (Unless you want to argue that SN 1987A never happened?)
Another “direct” method for measuring the Hubble Constant is using time delays of brightness variations between multiply lensed image (of the same background source) in a gravitational lens system. These have generally produced estimates of H_0 between 50 and 100. (There are unfortunately a lot of assumptions about the mass distribution of the lensing system that have to be made (as well as assuming that the background source is pointlike), which is probably why there’s so much variation.)
“Another “direct” method for measuring the Hubble Constant is using time delays of brightness variations between multiply lensed image (of the same background source) in a gravitational lens system. “
Yes. I helped write a paper on this, and also talked about some of the uncertainties due to other cosmological parameters as well as the fact that the universe is not completely homogeneous at this conference.
One can, of course, use gravitational lensing to determine other cosmological parameters as well. I’m an author or co-author and several such papers; the JVAS analysis probably gives the best flavour.
Why do so few talk about this anymore? Basically because systematic uncertainties are much larger than those of more modern tests such as the m–z relation from type-Ia supernovae (where it seems that we don’t have to worry about small-scale inhomogeneities and can even say something about how dark matter is distributed), the CMB, and BAO.
Of course, back when this work (determining cosmological parameters via gravitational lensing), none of the more precise tests had produced any interesting results, and for a while gravitational lensing actually had the lead. This is probably now of interest mostly to historians of science, though. I was even on a paper using lensing to set a lower limit on the cosmological constant. OK, the limit was negative, but it might be the first paper to set such a limit which didn’t turn out to be based on data which were later shown to be too imprecise or just wrong. What was the first paper to actually set limits on the cosmological constant from observational data? Does anyone know of an older one than the one by Solheim?
Interestingly, the time-delay paper linked to above concluded that the Hubble constant was 69. How right we were, and that 20 years ago!
To be fair, the actual claim was 69+13/-19 km/s/Mpc at 95 per cent confidence. Later work showed that at least the error estimate and perhaps the value itself were wrong, or at least should be modified in a better analysis (which, of course, has been done). We nevertheless got the right answer since various errors in different directions cancelled. However, in the words of Henry Norris Russell, “A hundred years hence all this work of mine will be utterly superseded: but I am getting the fun of it now. “
Sean or Scott Hughs,
Can the mass of each NS, or the total combined mass of the binary system, be derived from the GW chirp, perhaps in conjunction with other EM data, in a way that it couldn’t be derived with only EM data? Or only the rate of change of the mass quadrupole.
Darrell Ernst: The EM data alone from an event like this doesn’t tell us too much specifically about the masses involved. Basically, we know a lot of material went “boom” or “splat.” The fact that there are lots of models suggesting ways to produce short-hard gamma ray burst explosions points to the fact that from the EM measurements alone, some of the key pieces needed to constrain models was missing. The light curves afterwards tell us quite a bit about the material that was created by r-process nucleosynthesis (e.g., from the radioactive decay of heavy elements), including roughly how much mass was ejected from the system. So that’s partial information, but leaves out a lot of details, especially regarding the total mass of the system.
The minute and a half of chirping inspiral encodes a certain combination of the masses of the two neutron stars (the “chirp mass,” so-called because it controls the rate at which the binary’s frequency chirps) to high precision — GW170817 has a chirp mass of 1.188 solar masses, with roughly 0.3% error bars. There’s a moderately wide range of individual neutron star masses that are consistent with this chirp mass, which is why the reported individual neutron star masses span a somewhat wide range. The results also depend upon what kind of binary models one uses. When you examine the papers you’ll see different numbers depending on whether the models allow “high spins” or assume “low spins.” Low spins are consistent with binary neutron stars that are observed as radio pulsars in the galaxy, and so there’s a strong plausibility case that nature likes this. However, the laws of physics don’t forbid high spins, so its worth examining that case too and seeing how things change.
Scott,
Thank you for the explanation and taking the time to write it. I appreciate it.
Darrell, you’re welcome! (I once participated in blog discussions quite a bit, but basically took a hiatus a few years ago. Discussions like this remind me of how fun it can be.)
I’ve been an ill-informed cynic on this LIGO business. Basic questions from someone not too bright or well-informed. I’m wondering how good the three interferometer arrays, without other detectors but combined, are considered to be at directionality? Is the assumed correspondence to the same event based primarily on time alignment with the other signals or on spectral content of the event as expected/modeled, or both?
Simon Packer: by themselves, the GW interferometers pin down source position to a fairly large chunk of sky. GW170817 was localized to a part of the sky that was about 20 square degrees in size, which is something like 40 times the size of the full moon. This is one of the reasons we like to think of GWs as sound-like, and the detectors as ear-like: When we hear something, we get a rough idea of where that something is, so we turn our heads and look to try to pin it down more precisely. Similarly, the LIGO-Virgo localization was good enough that we could point telescopes. It only took a few minutes before optical telescopes found a large galaxy in the region of GW localization that showed a bright light source that had not been present earlier (shown in the images that Sean reproduces here).
You ask about the basis for the assumed correspondence, bringing up a couple of reasons why it might make sense. The best reason I can give you is “all of the above, plus more.” It’s the time alignment; the fact that the event was smack in the GW localization region; the fact that the GW data properties only fit if the event comes from two merging neutron stars, and the event has many of the predicted electromagnetic features we expect from two merging neutron stars.
Thanks Scott.
I take it you are close to the project. BTW I make 20 square degrees to be nearer 100 full moons in subtended area. Anyway a few degrees across. Do all these events so far have GW spectral content in the same frequency window (i.e. low audio frequency)? I assume the arrays and instrumentation are optimized for a certain bandpass based on anticipated event models?
Simon Packer: Whoops, you’re dead right on the area … the full moon is roughly 1/4 a square degree. I should have caught that when I proofread my comment before hitting submit!
Yes, all of the events measured so far have spectral support in what turns out to be low audio. The sensitive band of terrestrial GW detectors is controlled on the low end by ground vibrations, and on the high end by photon counting statistics. Below about 5 or 10 Hz, vibrations of the Earth will overwhelm any GW signal. (That’s true even with a perfect vibration isolation system because it turns out that the detectors can couple *gravitationally* to ground vibrations! I studied this as part of my PhD work.) Above a few thousand Hertz, and the graininess of photons in the laser beam comes into play. When we measure a signal at frequency f, we effectively average the signal for a time 1/f. When we average our measurements for short time intervals, the fact that a laser beam contains discrete photons becomes important: one interval might have a billion photons, the next a few thousand fewer, then next a few thousand more, etc. These fluctuations act as a source of noise, limiting sensitivity at high frequency.
With technology dictating low audio as the sweet spot for terrestrial detectors, the question became “What sources can we see (or hear) in the window we can use?” Thankfully, nature was kind, and it turned out things with masses from about 1 sun up to a hundred or so suns generate signals in the band of detectors like LIGO and Virgo.
If you want to look (or listen) to a different band, you’ve got to change how you do the measurements. Objects with millions of solar masses (like the black holes in the cores of galaxies) are expected to have interactions that generate really strong GWs, but at much lower frequencies: roughly 0.0001 Hz up to 0.1 Hz. Such signals correspond to sources with orbital periods of hours or minutes. There’s no way to make an Earth-bound detector that can measure this, so people are thinking of ways to make such measurements using spacecraft. This has led to LISA, the Laser Interferometer Space Antenna (see sci.esa.int/lisa and lisa.nasa.gov), a mission that is quite dear to me – a good chunk of my career has been spent thinking about LISA sources and LISA astronomy. Hopefully it will fly before I retire; space astrophysics missions are not for the impatient.
A technique which we expect will allow us to probe processes involving even more massive black holes that we see in the cores of galaxies is based on very long-term timing of highly regular signals from radio pulsars. There’s an active community of researchers working right now to find signals with periods of months or even years by monitoring radio pulsars over many years (decades in some cases). The American collaboration working on this is the “North American Nanohertz Observation for Gravitational Waves,” or “NANOGrav” (nanograv.org).
Much like in telescope-based astronomy, the constraint of being on the Earth’s surface dictates what the detectors can see (or hear). Optical telescopes see through our atmosphere; it’s harder to see through in other wave bands, and impossible in some (e.g. in x-rays). To see in x-rays, we have to go to space. For GWs, we can hear the audio band GWs with terrestrial detectors like LIGO and Virgo. But, there’s a lot of science at much lower frequencies, so we either need to go into space with LISA, or use “detectors” made out of astronomical objects like pulsars.
Thanks again for the comprehensive reply. I find the cosmology fascinating and know little about it.
I appreciate the band-pass restrictions based on unavoidable physics at HF and seismic at LF.
The following assumes I know roughly how you did this with LIGO. I was questioning a little the signal extraction not knowing how far down it is in level compared to a 90 degree interferometer phase shift and where the maximum practical noise floor is. As soon as you decide on a phase difference signal pass-band, you are presumably implementing a data filter in DSP. A fast roll-off filter will generally produce time domain ringing on any impulse, at a frequency near the cutoff. With the signal being near the noise floor, random noise can produce excitation with occasional strongly defined spectral content in the short term. Is everyone now truly confident that the detection stats are correct and the events truly significant? Some had doubts over this. Is the magnitude of the astrophysical events comparable to the anticipated design limit?
(I once worked for a company which made a military switchmode power supply that had to coast on stored charge when the attached receiver required highest sensitivity. EM environment is noisy these days).
Hi Simon: I’m not one of the people who is deep in the guts of the data analysis, so I’m not really the right person to answer these questions (I’m a theorist who focuses on modeling sources and thinking about what kind of general detector characteristics one needs to measure sources). A lot of the details germane to answering your questions can be found in the various papers the collaboration has published, but it’s not really in my wheelhouse.
In lieu of a detailed answer on the DSP aspects (for which I might be able to choke out an answer, but I’m just not confident in getting the details right), I’ll just comment that the astrophysical events are not unexpected. The major surprise seems to be that they are in line with the more optimistic end of astrophysical estimates that were made before advanced LIGO started operating. For example, catching a binary neutron star merger that is “only” about 40 megaparsecs away is a bit surprising. Either the rates are higher than our best astrophysical estimates suggested they would be, or we got lucky and caught one that is closer to us than we expect is typical. If the latter, then we’ll probably have a bunch more such events in the next observing run. Time will tell.
Whoops, error in my previous comment: If the _former_ (ie if the rates are higher than we had thought), then we’ll probably have a bunch more events in the next observing run.
Thanks Scott
I appreciate your time and straightforward responses. I know efforts have been made to open up the data processing to general examination and I haven’t looked at it all carefully. It’ll certainly be interesting to see what the future brings with the detectors.
I once heard that, when multiple people come up with the same idea, it usually means they stole it from someone else, or it was an inevitable natural conclusion based on the ongoing march of science.