This year we give thanks for an area of mathematics that has become completely indispensable to modern theoretical physics: Riemannian Geometry. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, gauge symmetry, Landauer’s Principle, and the Fourier Transform. Ten years of giving thanks!)
Now, the thing everyone has been giving thanks for over the last few days is Albert Einstein’s general theory of relativity, which by some measures was introduced to the world exactly one hundred years ago yesterday. But we don’t want to be everybody, and besides we’re a day late. So it makes sense to honor the epochal advance in mathematics that directly enabled Einstein’s epochal advance in our understanding of spacetime.
Highly popularized accounts of the history of non-Euclidean geometry often give short shrift to Riemann, for reasons I don’t quite understand. You know the basic story: Euclid showed that geometry could be axiomatized on the basis of a few simple postulates, but one of them (the infamous Fifth Postulate) seemed just a bit less natural than the others. That’s the parallel postulate, which has been employed by generations of high-school geometry teachers to torture their students by challenging them to “prove” it. (Mine did, anyway.)
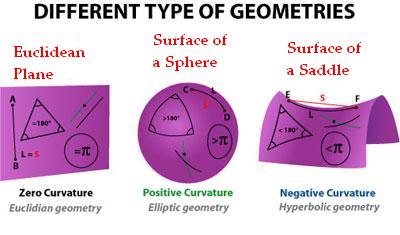
It can’t be proved, and indeed it’s not even necessarily true. In the ordinary flat geometry of a tabletop, initially parallel lines remain parallel forever, and Euclidean geometry is the name of the game. But we can imagine surfaces on which initially parallel lines diverge, such as a saddle, or ones on which they begin to come together, such as a sphere. In those contexts it is appropriate to replace the parallel postulate with something else, and we end up with non-Euclidean geometry.
Historically, this was first carried out by Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Lobachevsky, both of whom developed the hyperbolic (saddle-shaped) form of the alternative theory. Actually, while Bolyai and Lobachevsky were the first to publish, much of the theory had previously been worked out by the great Carl Friedrich Gauss, who was an incredibly influential mathematician but not very good about getting his results into print.
The new geometry developed by Bolyai and Lobachevsky described what we would now call “spaces of constant negative curvature.” Such a space is curved, but in precisely the same way at every point; there is no difference between what’s happening at one point in the space and what’s happening anywhere else, just as had been the case for Euclid’s tabletop geometry.
Real geometries, as takes only a moment to visualize, can be a lot more complicated than that. Surfaces or solids can twist and turn in all sorts of ways. Gauss thought about how to deal with this problem, and came up with some techniques that could characterize a two-dimensional curved surface embedded in a three-dimensional Euclidean space. Which is pretty great, but falls far short of the full generality that mathematicians are known to crave.
 Fortunately Gauss had a brilliant and accomplished apprentice: his student Bernard Riemann. (Riemann was supposed to be studying theology, but he became entranced by one of Gauss’s lectures, and never looked back.) In 1853, Riemann was coming up for Habilitation, a German degree that is even higher than the Ph.D. He suggested a number of possible dissertation topics to his advisor Gauss, who (so the story goes) chose the one that Riemann thought was the most boring: the foundations of geometry. The next year, he presented his paper, “On the hypotheses which underlie geometry,” which laid out what we now call Riemannian geometry.
Fortunately Gauss had a brilliant and accomplished apprentice: his student Bernard Riemann. (Riemann was supposed to be studying theology, but he became entranced by one of Gauss’s lectures, and never looked back.) In 1853, Riemann was coming up for Habilitation, a German degree that is even higher than the Ph.D. He suggested a number of possible dissertation topics to his advisor Gauss, who (so the story goes) chose the one that Riemann thought was the most boring: the foundations of geometry. The next year, he presented his paper, “On the hypotheses which underlie geometry,” which laid out what we now call Riemannian geometry.
With this one paper on a subject he professed not to be all that interested in, Riemann (who also made incredible contributions to analysis and number theory) provided everything you need to understand the geometry of a space of arbitrary numbers of dimensions, with an arbitrary amount of curvature at any point in the space. It was as if Bolyai and Lobachevsky had invented the abacus, Gauss came up with the pocket calculator, and Riemann had turned around a built a powerful supercomputer.
Like many great works of mathematics, a lot of new superstructure had to be built up along the way. A subtle but brilliant part of Riemann’s work is that he didn’t start with a larger space (like the three-dimensional almost-Euclidean world around us) and imagine smaller spaces embedded with it. Rather, he considered the intrinsic geometry of a space, or how it would look “from the inside,” whether or not there was any larger space at all.
Next, Riemann needed a tool to handle a simple but frustrating fact of life: “curvature” is not a single number, but a way of characterizing many questions one could possibly ask about the geometry of a space. What you need, really, are tensors, which gather a set of numbers together in one elegant mathematical package. Tensor analysis as such didn’t really exist at the time, not being fully developed until 1890, but Riemann was able to use some bits and pieces of the theory that had been developed by Gauss.
Finally and most importantly, Riemann grasped that all the facts about the geometry of a space could be encoded in a simple quantity: the distance along any curve we might want to draw through the space. He showed how that distance could be written in terms of a special tensor, called the metric. You give me segment along a curve inside the space you’re interested in, the metric lets me calculate how long it is. This simple object, Riemann showed, could ultimately be used to answer any query you might have about the shape of a space — the length of curves, of course, but also the area of surfaces and volume of regions, the shortest-distance path between two fixed points, where you go if you keep marching “forward” in the space, the sum of the angles inside a triangle, and so on.
Unfortunately, the geometric information implied by the metric is only revealed when you follow how the metric changes along a curve or on some surface. What Riemann wanted was a single tensor that would tell you everything you needed to know about the curvature at each point in its own right, without having to consider curves or surfaces. So he showed how that could be done, by taking appropriate derivatives of the metric, giving us what we now call the Riemann curvature tensor. Here is the formula for it:
This isn’t the place to explain the whole thing, but I can recommend some spiffy lecture notes, including a very short version, or the longer and sexier textbook. From this he deduced several interesting features about curvature. For example, the intrinsic curvature of a one-dimensional space (a line or curve) is alway precisely zero. Its extrinsic curvature — how it is embedded in some larger space — can be complicated, but to a tiny one-dimensional being, all spaces have the same geometry. For two-dimensional spaces there is a single function that characterizes the curvature at each point; in three dimensions you need six numbers, in four you need twenty, and it goes up from there.
There were more developments in store for Riemannian geometry, of course, associated with names that are attached to various tensors and related symbols: Christoffel, Ricci, Levi-Civita, Cartan. But to a remarkable degree, when Albert Einstein needed the right mathematics to describe his new idea of dynamical spacetime, Riemann had bequeathed it to him in a plug-and-play form. Add the word “time” everywhere we’ve said “space,” introduce some annoying minus signs because time and space really aren’t precisely equivalent, and otherwise the geometry that Riemann invented is the same we use today to describe how the universe works.
Riemann died of tuberculosis before he reached the age of forty. He didn’t do bad for such a young guy; you know you’ve made it when you not only have a Wikipedia page for yourself, but a separate (long) Wikipedia page for the list of things named after you. We can all be thankful that Riemann’s genius allowed him to grasp the tricky geometry of curved spaces several decades before Einstein would put it to use in the most beautiful physical theory ever invented.
A triangle should be re defined in the new geometry. It is the angles turned through … In all planes ..3dimensionally
Start at North Pole ..head south to equator ..in one straight line .
You have moved on a curve thro 90 Degrees … Just by going in a straight line
Turn left 90 At the equator… Go one quarter round then face north
You have moved thro another 90
Now go north to pole … You walk in astraight line …but also you turn 90. Over curve of earth
That is 3 X 90
Plus the 3 X 90
So you really move thro 6 X 90 = 540 degrees
Of movement in 3 D
But you have gone through 360 degrees of earth curvature
So 540 – 360 = 180
There is your triangle
Internal angles 180
But re define triangle …or stipulate dimensions of curvature
Simple eh
For those who would like to know more about Riemann, at least to get from alpha to zeta, I recommend the popular biography “Prime Obsession”, by John Derbyshire.
With Derbyshire’s account mentioned, I think it only fair to point out 3 other popular accounts of Riemann’s most important finding:
“The Music of the Primes” by Marcus du Sautoy
“Stalking the Riemann Hypothesis” by Dan Rockmore
“The Riemann Hypothesis” by Karl Sabbagh
All have different strengths and weaknesses, and all are written for a general audience.
Thank you Dr. Carroll for another cool article! As an amateur physics enthusiast I love to read about the personal stories of these great thinkers as much as trying to appreciate their vast contributions.
Great post Sean.
Have you ever visited the Mathematics and Physics museums at the University of Göttingen? I live pretty close to it, and it is really an amazing collection that shows you how these people visualized these types of things before computers ( http://modellsammlung.uni-goettingen.de/ )
(In case anyone doesn’t know what Göttingen has to do with math and physics, it was (and still is) the home to a long, illustrious line of physicists, mathematicians, and chemists, including Georg Riemann, Carl Gauß, Max Born, Hermann Minkowski, Werner Heisenberg, David Hilbert, Max Planck, Karl Schwarzschild, Felix Klein, Wolfgang Pauli, Enrico Fermi, Irving Langmuir, Wilhelm Weber, J. Robert Oppenheimer, Alfred Clebsch, James Franck, Max von Laue, John von Neumann, Otto Wallach, Friedrich Wöhler, Walther Nernst, Richard Courant, Peter Debye, Constantin Carathéodory, Hans Dehmelt, Peter Dirichlet, Manfred Eigen, Carl Glaser, Maria Goeppert-Mayer, Otto Hahn, Edmund Landau, Carl Runge, and many others (not to mention the doctors, biologists, writers, poets, etc).)
One could add that the impact of Riemannian geometry in physics goes beyond general relativity: If I understand correctly, gauge theory is centered around the notion of connection on principal bundles, which is a generalization of the Levi-Civita connection and parallel transport of Riemannian geometry. (That part of Riemannian geometry was only developed after he died, though.)
Since they found that the rate of exponential expansion of the universe is increasing, does that mean that elliptic geometry is going to be completely useless? I was under the impression that studies done on the curvature of the universe have shown that a closed universe would need elliptic geometry and an open universe would require use of hyperbolic geometry. Then a universe which had the exponential rate of expansion stay the same would require Euclidean Geometry. Then watching a video about how they received the noble prize for that discovery, they just mention that the type of geometry doesn’t even matter, because the distances were so large that it wasn’t significant (which seems really counter intuitive). Then they only tested the rate of expansion using Euclidean Geometry. Really couldn’t help but think, “shame on them”. We got all of these “useless” geometries that no one even cares to use, even when doing experiments which could determine the shape of the universe…
Dead at 40!? With a beard like that? And I used to think t I was jealous of his mathematical accomplishments…
I’ve been reading your Thanksgiving posts every year for the past decade. They are truly one of the most pleasant things I look forward to every holiday season. May this tradition lasts as long as it can be! Maybe one day these can all become a book, or something to immortalize the writings for generations ahead!
Thanks again, for another excellent piece!
Sean, I second Harold’s appreciation of your Thanksgiving posts, assuming this one is fairly typical. For me, the real nugget was the 7 sentences beginning with “Finally and most importantly,…”. They gave me the (ok, perhaps illusory:-) feeling that I understood Reimannian geometry about as well as any layperson, whereas 2 minutes earlier I’d been pretty clueless. I’m motivated to find similar such nuggets on other topics – and I know just where to begin looking:-)
Glad people like the posts!
Another wonderful post, thank you Sean.
As mentioned in the linked talk about Einstein, sometimes theory and research may not make their usefulness apparent in their time, here is a another great example of how science and humanity have benefited by the somewhat unheralded work of (unfairly) lesser known pioneers.
They say that mathematics has always been far more advanced than physics, and physics has always just been making use of advancements in mathematics later on to try to catch up to it. Who knows? One day our great grandchildren will find it more useful, and he will be hailed as one of the biggest contributors in future modern physics. Then I guess someone would have to keep the story alive in order for that to happen, so they wouldn’t have to reference something hundreds of years old, lol.
I still think it would be interesting if someone discovered that the exponential expansion rate of the universe wasn’t increasing in hyperbolic space or something. That would be a real brain bender… Then I think this topic has been a little over done in a lot of books designed for laymen.
We dpn’t doThanksgiving in Oz, but I will certainly buy into giving thanks to Riemannian Geometry.
Incidentally, here is a gentle but thorough treatment of tensor analysis from NASA that I found useful:
http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20050175884.pdf
Here is a very nice illustration of the various projections of non-Euclidean spaces onto Euclidean space: https://www.youtube.com/watch?v=eGEQ_UuQtYs