Last week I had the pleasure of giving a seminar to the philosophy department at the University of North Carolina. Ordinarily I would have talked about the only really philosophical work I’ve done recently (or arguably ever), deriving the Born Rule in the Everett approach to quantum mechanics. But in this case I had just talked about that stuff the day before, at a gathering of local philosophers of science.
So instead I decided to use the opportunity to get some feedback on another idea I had been thinking about — our old friend, the claim that The Laws of Physics Underlying Everyday Life Are Completely Understood (also here, here). In particular, given that I was looking for feedback from a group of people that had expertise in philosophical matters, I homed in on the idea that quantum field theory has a unique property among physical theories: any successful QFT tells us very specifically what its domain of applicability is, allowing us to distinguish the regime where it should be accurate from the regime where we can’t make predictions.
The talk wasn’t recorded, but here are the slides. I recycled a couple of ones from previous talks, but mostly these were constructed from scratch.
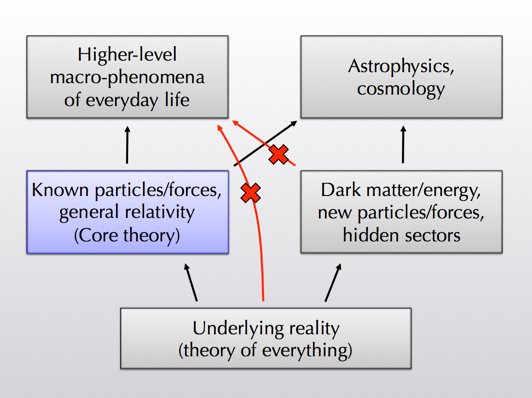
The punchline of the talk was summarized in this diagram, showing different regimes of phenomena and the arrows indicating what they depend on:
There are really two arguments going on here, indicated by the red arrows with crosses through them. These two arrows, I claim, don’t exist. The physics of everyday life is not affected by dark matter or any new particles or forces, and its only dependence on the deeper level of fundamental physics (whether it be string theory or whatever) is through the intermediary of what Frank Wilczek has dubbed “The Core Theory” — the Standard Model plus general relativity. The first argument (no new important particles or forces) relies on basic features of quantum field theory, like crossing symmetry and the small number of species that go into making up ordinary matter. The second argument is more subtle, relying on the idea of effective field theory.
So how did it go over? I think people were properly skeptical and challenging, but for the most part they got the point, and thought it was interesting. (Anyone who was in the audience is welcome to chime in and correct me if that’s a misimpression.) Mostly, since this was a talk to philosophers rather than physicists, I spent my time doing a pedagogical introduction to quantum field theory, rather than diving directly into any contentious claims about it — and learning something new is always a good thing.
Bostontola,
Yes, well, Galileo is dead, so we cannot possible know what he would do. Rhetorical question, of course.
It is possible that a newer, more general theory will agree with all evidence gathered so far, but will make a novel prediction for gravity-induced motion inside ordinary bodies of matter. For gravitational purposes, your “definition” of everyday life thus implicitly excludes the insides of ordinary bodies of matter. Or else you presume to know beforehand that current theories will agree with what we would find when we finally get around to testing gravity inside ordinary bodies of matter (Galileo’s experiment).
But all this quibbling is tiresome and inconclusive. Why not let Nature do the talking? The “limits of our knowledge” are blemished by the huge gap in our empirical knowledge of gravity. By pointing this out I hope that the curiosity of some readers may have been piqued. Someday, somebody will see fit to perform Galileo’s experiment. Given its relatively low expense and its feasibility, it seems silly for physicists to wait any longer. Why be satisfied with a guess as to the experiment’s result when we could replace the guesswork with an empirical fact?
Finally, wouldn’t it be cool to see an utterly fundamental demonstration of gravity in action that no human has ever seen before? Wouldn’t it be beautiful to behold? Alas, the childlike sense of wonder seems to have gotten sadly rare.
I feel that Quantum Theory needs to look at the Mathematics that it is using. It uses Equations just because they provide the ‘right’ answer. But these equations are basically nonsense from a mathematical point of view.
An example is:
1+2+3+4+ … =. – 1/12
@David
I think the developers of quantum theory where a little more picky than that. According to Brian Green, they have not agreed on a correct way to deal with infinite series. It has been held back from string theory as well. It has been mentioned in Brian Greens new book that finding a correct way to add infinite series together could help find out a lot in string theory. Then I have also heard of some ways that they can be added together, and adding all the whole numbers could get you something like -1/12. Then even though it is taught to be correct by some people, it really has not be proven to be right. You can get a range of different answers by choosing to add or subtract different sets of number or by changing the order of operations. Most likely, -1/12 is the wrong answer, even though it can be found through some process. The process it was found would just be wrong. I mean look at it. It is -1/12, and your adding positive whole numbers!
Then in this video. It claims it is used in string theory. Then look at the first example. S =1-1+1-1+1… = 1/2
You would start with 1 and then you would get either 1 or 0 depending where you ended, so they take the average of 0 and 1 to get 1/2. Say you started with a negative one instead of the positive one. You would get -1/2, because you would either get -1 or 0 depending where you ended. The average of 1/2 and -1/2 would then be 0… It just depends where you want to start or finish. Funny though, it would seem like you could get the right answer taking the average of both averages of start and finish locations. An easier way would be just taking the average of 1 and -1.
https://www.youtube.com/watch?v=w-I6XTVZXww
herb wiggins, MD: “Frankly, the laws of physics are NOT understood, and may never be. Godel’s Incompleteness Theorem, also misnamed “Godel’s Proof”, shows this cannot be the case using recursive, reiterative logic and maths, of which physics is replete with examples.”
I’m not so sure you can apply Godel’s Theorems to physics, though I once thought so.
The problem is that the theorems apply in the context of mathematical theories that are at least as comprehensive as Peano arithmetic. My understanding is that it does not necessarily apply to less comprehensive systems. Is the Universe that comprehensive? If the Universe is finite (and also only finitely divisible), then there is an upper bound to numbers that it can comprehend. (We can describe Graham’s number, for example, but it is entirely possible — and in my mind, very likely — that our Universe of only 10^80 or so particles can never actually compute it, yet it is still in the reach of Peano arithmetic. The multiverse, on the other hand, may be large enough to do that.)
Therefore it may be (but is not necessarily) the case that all questions of physics are, in principle, decidable, and that there is, in principle, a comprehensive theory of physics. At best, it is an open question.
You’ve stated in both “The Particle at the End of the Universe” and your great courses lecture “The Higgs Boson and Beyond” that one of the issue you encounter is background “noise”. I believe in the great courses lecture you even made a point to stress that where the higgs sits is really THE spot where the background is the worst. Would you please elaborate on why you stressed that point?
Would extinction events count as everyday??
Lisa Randall and Matthew Reece, “Dark Matter as a Trigger for Periodic Comet Impacts,”
Phys. Rev. Lett. 112, 161301 (2014)
“Would extinction events count as everyday?”
I hope not. I had plans for the rest of the day.
As mentioned previously, the Big Bang doesn’t count either. Just stuff we could expect to encounter any day.
Sean,
Great stuff. I have a suggestion for your next talk with philosophers – give your views on Jenann Ismael’s talk “On Why We See the Past as Fixed and the Future as Something We Can Bring About by Will: the View Through the Lenses of Physics” (starts at 00:56). It’s a video, sadly, but worth your time I think. Ismael also wrote a paper I think you’ll like, which anticipates the move you and Chip Sebens made about Self-Locating Uncertainty as the source of probability in EQM. Which isn’t related, but might convince you that she’s worth a listen.
Paul– Thanks for those links. I know Jenann, and think she’s well worth listening to!