Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
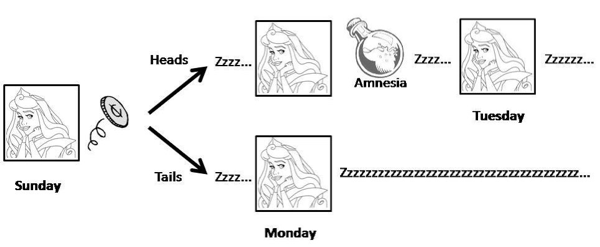
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
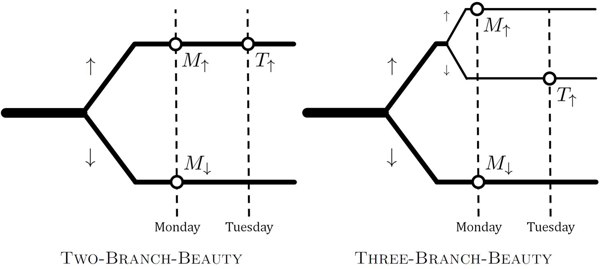
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
Logicophilosophicus, you deduced betting conventions from a “universal understanding” that is itself an external proposition to the problem. It’s a non sequitur, again analogies are not helping your argument. Stick with the math, which is the formal translation of the problem. As for my statement, yes I meant to say “already transpired,” haha, don’t know why I said the opposite. Clearly an actual bet usually takes place before the chances have played out.
My understanding of P(H|I) is exactly as calculated in my very first comment. It’s equal to P(I|H)*P(H)/P(I). P(I|H) is clearly the probability of the interview given the coin flip is heads, which is equal to 1 in this problem. P(I)=3/4 since P(I|Wake_1 & H) = 1, P(I|Wake_1 & T) = 1, P(I|Wake_2 & H)= 1, P(I|Wake_2 & T) = 0. So using arithmetic, I’m dividing 1/2 by 3/4, which is 2/3.
Philosophicus, you wrote:
“p(H|I) seems to be the probability of getting a heads result given that an interview has already taken place. How does the protocol allow that sequence? There’s more that a hint of time travel there.”
Thanks, that insight makes everything perfectly clear. I can now state with full confidence that “The Sleeping Beauty problem is a probability puzzle that separates people into two groups: those who understand conditional probability, and halfers.”
You also wrote this:
“To reason backwards in time is a little odd, but just because SB can’t tell the difference between these three actually quite distinct interviews cannot make the I in the second branch lead back to an H in the first branch (we can’t jump from one branch to another); nor especially can it make the two I’s in the first branch lead back to two H’s, creating a third branch out of nowhere. Reasoning back in time from, say, the second I in the Heads branch leads back through the first I to the single H.”
Thanks to that masterful deconstruction, we can now dismiss the whole silly “science” of forensics and empty the prisons of those it has wrongly been used to convict.
As nobody with a grasp of conditionalization has answered any of my three challenges with a viable defense of halferism, the thirder position is unvanquished. Game, set, match. My work here is done.
George Ellis, provided the measurement guarantees that the pre-measurement state is unchanged by the measurement and as long as the Hamiltonian is not separable in the observables corresponding to the apparatus, environment, observer, and target, then you cannot break up the tensor products to analyze unitary evolution. It is certainly possible that:
U(t-t’)(|up> + |dn>)⊗|A_o> = (|up>⊗|A_up> + |dn>⊗|A_dn>)
This can very well be a result of unitary evolution. The state,
(|up> + |dn>)⊗|A_o>, can be uniquely recovered by time reversal of
(|up>⊗|A_up> + |dn>⊗|A_dn>) under the same unitary operator. In this case, clearly the unitary operator U cannot be decomposed onto U_spin and U_apparatus unitary operators.
However when coupling to the environment and assuming a general initial state (mixed or coherent superposition), asserting that the nondiagonal entries vanish is not as defensible.
Regarding Logicophilosophicus, I didn’t even notice his interpretation that P(H|I) is “heads following an interview” in time. Rest assured, I think LP has acknowledged his unfamiliarity with conditional probabilities.
Correction to/clarification of above, meant to say it’s not as defensible that the off-diagonal entries (when traced over the environment) vanish.
p(H|I) – which “I”?
You both needed to look at those independent branches. There is no die or coin or roulette wheel where the 3 I’s are presented for selection and have similar connections to H. The I in the T->I branch precludes H. The second I in the H… branch is 100% dependent on H->I…
The SB and the BS both know that the fact of waking does not change the probability of Heads, because they experience the confusion but also know the protocol. You are both apparently incapable of realising that the conclusion that H is always more probable than tails is paradoxical, which as Euclid could tell you means that (assuming the symbolic manipulation obeys the rules) means that the premisses are at fault (GIGO).
I pointed out that you both attribute assertions to me which are the opposite of what I stated, but get no explanation. I asked for some fairly straightforward explanations but you prefer to be abusive.
Well, boys, enjoy. I’m out of here.
[Ironically, the typical problem with forensic evidence is the conditional probability fallacy. Not that that is the problem here.]
Logicophilosophicus, there’s no abuse here, I’m not disliking your comments solely because I disagree with them, I’m not disliking them at all actually. Conditional probability has nothing to do with time in the same sense logical inference does not. I preceding H/T is not a problem. Again, the problem is not asking you to determine the probability of a coin flip given this experiment, that is clearly 1/2 no matter what. The problem is asking you to determine the most likely outcome given the sampling scheme SB undergoes in the experiment. There is no reason why this is necessarily 1/2 independent of whatever the experiment is. We’re not saying an absolute coin flip has higher odds of Heads because of how you observe it, we’re saying that how you selectively count the result of coin flips will affect the apparent odds you measure.
Daniel, I think when he mentioned “conditional logic fallacy”, he was intending to mean the base rate fallacy. I don’t know why he thinks that is ironic. The base rate fallacy is a fallacy committed by those who don’t understand conditionals, not by those who do (unless they are careless). So it is ironic that he brought it up, but it is not ironic in the context of valid arguments about conditionality.
I don’t know what statement I attributed to him that he did not actually make so I can’t respond to that accusation.
On the whole, he is committing a petitio principii fallacy, as shown by his last post:
“You are both apparently incapable of realising that the conclusion that H is always more probable than tails is paradoxical, which as Euclid could tell you means that (assuming the symbolic manipulation obeys the rules) means that the premisses are at fault (GIGO).” Translation: The logical conclusion is inconsistent with halferism; halferism is correct (therein lies the petitio ptincipii); this means that the logical conclusion that halferism is wrong must be based on erroneous premises; therefore, halferism must be right after all.
Had he wished to engage in an honest argument, he could challenge any of the anti-halfer assumptions, independently of conclusions. This has been tried: I have seen an article advocating rejection of the assumption that one can conditionalize on temporally indexed discoveries (or as a corollary, losses of information such as what SB experiences). Certainly he could have gone that route, but ultimate acceptance requires changing the standard axioms of probability and so would require a stronger case than was made in that article.
Richard, I was forgetting the name of that fallacy, thanks! Like I said in a previous comment, he assumed the conclusion from the beginning. Still, it reaffirmed my understanding of it by tackling these fallacies, so I got something from the discussion whether it was honest or not.
I’m interested in Ellis’s post above more right now actually, wondering how justified orthogonality of the environment really is for a measurement where the measured object’s state is not changed by the measurement. For a weak measurement, one where the measured state would not be influenced, I definitely would think e1 and e2 would be highly correlated with each other and e0 except in the quantum numbers that correspond to the apparatus and observer states.
Amazing how much this has stirred up. We have only four outcomes possible. new information is knowing that she is awake thus only three outcomes are possible. Asking her the probability among each of four choices before she sleeps and asking her the probability when she knows only three equally probable choices remain changes her subjective probability from 1/4 to 1/3. Why is that wrong or difficult?
Pingback: Sleeping Beauty is smarter than most physicists | The Furloff
The correct probabilities
P(Tails given Tuesday) = 1
P(Tails given Monday) = 0.5
P(Heads given Monday) = 0.5
This is a pretty straightforward calculation.
http://thefurloff.com/2014/08/14/sleeping-beauty-is-smarter-than-most-physicists/
Pingback: Sleeping Beauty is strange but is still smarter | The Furloff
Hal, that blog has to justify why P(M)=2*P(T). See my calculation in my first comment for a correct application of conditional probabilities to the problem. I assumed P(M)=P(Tu), but P(I|M)=/=P(I|T), as in, I assumed that interviewing was a different set in the venn diagram than the days themselves. That Venn Diagram in that blog is too hastily put together, P(M)=P(Tu) in the experiment if you remove SB’s biased sampling from the problem. SB’s sampling should be yet another circle on the diagram overlapping H, T, M, Tu circles. The setup of the problem is thus incorrect as laid out in that blog.
Hal, Daniel’s points are correct.
I showed (Aug. 7, 3:46 pm post above) that the halfer position leads to an inconsistency (the conclusion that no interview can take place on Tuesday), given only the following assumptions, which most people will agree are reasonable given the problem statement:
p(H|MI) = 0.5
p(T|MI) = 0.5
(i.e., it should be equally probable that the toss was heads or tails, if SB is interviewed on a Monday, and these outcomes are mutually exclusive and exhaustive under that condition).
p(H|TuI) = 1.0
p(T|TuI) = 0.0
(i.e., it should be certain that the toss was heads and not tails, if SB is being interviewed on Tuesday).
I did not prove that the thirder position is correct. In fact, the above assumptions are not sufficient to show that it is. I did, however, show that the thirder assumption avoids the contradiction that the halfer assumption leads to. To prove the thirder position, you need the additional assumption that
p(M|I) = 2 * p(Tu|I)
although I think most people would also grant that this assumption is reasonable (twice as many interviews will take place on Monday as on Tuesday, given a large number of trials of the experiment).
Conditioning on interviews rather than days of the week allows for proper normalization of the calculated probabilities; it is not correct to say that Monday is twice as likely as Tuesday.
Richard
You don’t actually need that additional assumption (re-link).
Phayes,
I do see an assumption in your second set of equations:
Pr(Mon|.) = Pr(Mon|Heads, .) Pr(Heads|.) + Pr(Mon|Tails, .) Pr(Tails|.)
= Pr(Heads|.) + (1/2)*(1 – Pr(Heads|.))
(Heads/Tails roles are interchanged between your document and Sean’s statement of the problem.)
This requires that Pr(M|T,.) = 1/2, which is not explicitly given nor can it be derived from other givens. (Sure, it’s intuitively obvious, but we should declare our obvious intuitions as assumptions.) I believe it is equivalent to my additional assumption, although I don’t have time for the derivation right now.
Richard,
Yes it’s an assumption – at least it is if you regard the application of the principle of indifference here as an assumption rather than as a consequence of a consistency requirement [á la Jaynes, chap. II].
Richard, I derived the thirder position using only the following probability assignments:
P(Wake|Mon) = 1
P(Wake|H and Tue) = 1
P(Wake|T and Tue) = 0
P(H) = P(T) = 1/2
P(Mon) = P(Tue) =1/2
If the last one is the assumption you speak of, I’m not sure I’d agree that it’s an assumption. The days are a random variable in this problem with equal likelihood from the perspective of the experimenters (though ignoring their memories).
Pingback: Sleeping Beauty and the Importance of Wednesday | The Furloff
I have provided some more explanation of the correct calculation and what happens when Wednesday is excluded.
One thing I want to comment on. There appears to be a lot of confusion about how to include Tuesday into the calculation. The problem statement is pretty clear, the probabilities conditioned on Tuesday depend on whether Sleeping Beauty has been told its Tuesday. This is entirely from Sleeping Beauty’s vantage point. The probabilities would be different from an external observer’s vantage point who knew exactly what day it was. Sleeping Beauty has no knowledge of whether it is Monday or Tuesday unless she is told.
The other point of confusion, which I address in the article below is that Sleeping Beauties belief of the probability of heads is 50% unless she is told what day it is. The probability of a fair coin is not dependent on the day.
http://thefurloff.com/2014/08/15/sleeping-beauty-and-the-importance-of-wednesday/
Hal, you haven’t included SB in your Venn diagram at all though, you’ve skipped to collapsing it to her point of view. You have to build the Venn diagram as outlined by the experiment first, then draw SB’s circle overlapping the correct regions. You’ve skipped this step.
phayes,
Yes, I regard indifference as an assumption, for the sake of completeness. The argument I gave renders the halfer position inconsistent with the assumptions I originally gave, and compels the thirder position with the additional assumption. If halfers want to refute the thirder position, they only must deny one of the assumptions (including this one). If they want to assert their own position, they must deny one of my original assumptions — denying the indifference principle as applied to M/Tu probabilities is not sufficient for that purpose.
I don’t know of any argument that the principle of indifference is mandated for consistency, so my support for the principle of indifference is simply on the basis of common sense.
Daniel:
“P(Wake|Mon) = 1
P(Wake|H and Tue) = 1
P(Wake|T and Tue) = 0
P(H) = P(T) = 1/2
P(Mon) = P(Tue) =1/2”
Well, I would prefer to see things conditioned on interviews (or at least, on SB being awake), but I will assume that underlies these implicitly. Your first equation follows
directly from the problem statement. So do the second and third. The fourth is in the problem statement if the problem calls for a fair coin, but by convention I think we can agree that it is the intent if not stated otherwise.
I find p(M) = p(Tu) = 1/2 to be a little more problematic, since it doesn’t condition on being awake or being interviewed. I went with “p(M|I) = 2 * p(Tu|I)” to avoid questions about measures and normalization, or of how sampling bias is handled in the calculation (it expresses the bias explicitly and gives the same result). Phayes’s assumption “Pr(M|T,.) = 1/2” likewise avoids such issues. (By the way, I assume his “.” is the same as my “I”, and I know he is using H and T in the reverse sense of Sean’s version.) But yes, I would label it an assumption and not a given condition, lest someone comes along with a nonstandard notion of probability. Then they are free to deny it, but let them justify the denial.
Daniel,
I think its pretty clear in the problem statement that we are interviewing SB and not the interviewer.
Hal, in your third article you wrote:
“This means the probability of heads or tails given Monday changes dramatically.
P(H|M) = P(H & M)/P(M) = 0.5/0.66 = 0.75
P(T|M) = P(T & M)/P(M) = 0.167/0.66 = 0.25
The reason for the shift is that we are no longer allowed to consider P(T & M) to be a simple product of P(T) x P(M) . The correlations between the two mutually exclusive sets are too strong.”
This is the kind of error trap you can fall into when you don’t condition on the sampling criterion (what I called “I” for interview). You argued that P(H&M) = 0.5 because you did not allow for the equal overlaps (assuming indifference 🙂 between H and M and between H and Tu. That SB is not awake to witness the latter case, so that there is no “I” in “H and Tu”, is what brings the probabilities for the remaining combinations to 1/3 each when you conditionalize properly.
A Wednesday awakening isn’t relevant to SB’s calculation at all, assuming she will be told it’s Wednesday and no interview will take place on that day. Then when she is interviewed on Monday or Tuesday, she knows it isn’t Wednesday and does the calculation just as if there will be no Wednesday for her.
A question for halfers [perhaps some variant of this already appears in the thread]: Suppose that we change the SB puzzle, but only in the protocol for Tuesday after tails (T/t). The new protocol is that she is awakened as in the other cases, but, after a pause of a minute, is put back to sleep (but only on T/t). Again, she knows the full protocol in advance. In the first minute after awakening, she assigns equal probabilities for M/h, T/h, M/t, T/t. After a minute, if she is still awake, she excludes T/t and is left with equal probabilities for M/h, M/t, T/h. So in this case the 1/3 is correct. Do you agree with this result for the modified problem? If so, how can the changed protocol for T/t affect her relative weightings of the other three cases?
The main halfer argument is that when she awakens she gets no new information. But she does: by awakening she learns that the current situation is not T/t. In the modified puzzle, she gets the exact same information but in a different way.