Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
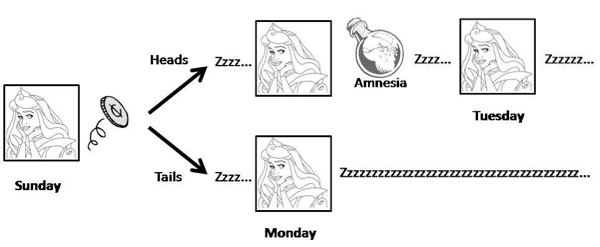
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
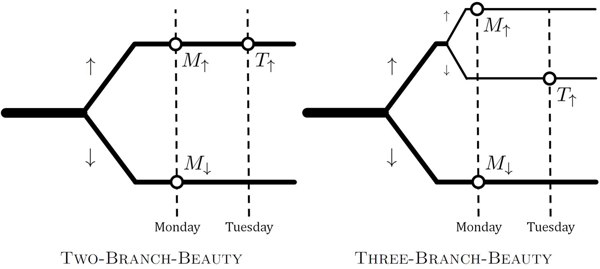
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
There’s been so much discussion, I’m not sure if this alternative procedure has been discussed:
Rules are similar, but with only one possible awakening. If the coin comes up heads, then she is woken and interviewed once on Monday. If the coin is tails, she is not woken up on Monday. If she is interviewed she is asked “What is the probability you would assign that the coin came up tails?”. Either way, on Wednesday she is woken up and told what happened. End of rules.
I hope we can agree that if interviewed she will be 100% sure it is heads, so the credence she gives to it being tails is 0?
By implication, this supports the P=1/3 answer to the question, as phrased on this blog (other blogs may have different versions!).
br,
You miss the point – basically you have written Monday’s business out of the protocol. Tuesday was always going to be definitive: result revealed. Monday was always going to be free of information about the toss result. The SB problem asks us to see what probabilistic conclusions, if any, she can draw from situations where Monday and Tuesday, or Before and After, are indistinguishable. Without that confusion there is no problem.
All these problems have evolved from the analysis of games of chance beginning in the 17th century. The point of assigning a probability is to determine the appropriate action – that’s as true of deciding which medicine to take as it is of deciding which card to bet on. Thirders think that SB’s decision to bet is influenced by her Monday-Tuesday confusion, and they are right, just not in the way they think. She should attempt to make a bet based on the known probabilities (assuming that the odds offered are favourable) whenever she is asked, so that she does not miss the opportunity to profit. She knows a Tuesday bet is impossible, but she just attempts to place a bet whenever asked, and thus always succeeds in making a (Monday) bet. She never gets to place two bets in the Heads timeline. In your scenario, she never gets to place one bet. In any related scenario, the probabilities (the ones she is asked to assign) are “in the coin”, not the protocol. Thirders are wrong.
Yes, my previous post was not exactly helpful – so I just downvoted it! 🙂
I came up with this statement though:
“I know the coin is fair so will come up heads in 1/2 of the trials. If I receive a dollar for each correct guess to the question ‘Is the coin I’m holding heads or tails?’, then remembering the structure of the trial (=information!) I should always pick heads, 100:0, to maximise profit. However I won’t be correct in all the guesses – with this strategy I believe 1/3 of the guesses will be wrong, averaged over many trials”.
Receiving money can be replaced by ‘maximising the number of truthful statements I make in my life’, a more noble aim. Then one needs to interpret the question “What is the probability you would assign that the coin came up tails?”, which is different than the one I just posed ‘Is the coin I’m holding heads or tails?’. The question ‘what is the probability…?’ can indeed be seen as a question about the coin, which has P=1/2 and knowledge of the structure of the trial won’t change this, whereas the betting question ‘Is the coin heads or tails?’ will be affected by the structure of the trial – as to maximise profit she will guess heads 100% but be wrong 1/3 of the time, which some might interpret to mean P=1/3. So this is a problem that can distinguish ‘pure’ probability from ‘betting’ probability?
Which I reckon makes thirders wrong, as P=1/3 doesn’t answer the question! (ducks for cover!)
Logicophilosophicus,
Please don’t insult my intelligence by suggesting that your “guess right or die” scenario was a fair bet. In fact she doesn’t even receive a payoff for guessing right. But more to the point, clearly she is under extreme duress if she accepted such terms. Or maybe she doesn’t want to live in the first place. After all it is a dreary life if the only thing that ever happens in it is you sleep or are being interviewed.
If you want to find a bookmaker who will offer a fair bet, find one who doesn’t have inside information (such as whether today is day 1 or day 2 of the experiment). For example, try the outside witness I talked about in an earlier post.
I made three separate cases for the thirder position. None require any assumptions about fair or favorable bets (I really don’t like to apply the gambling argument, since it is too easy to make mistakes similar to yours; Bayesian thinking is not so error-prone). Feel free to respond to any or all of them if you think you can make the halfer case as to why each is wrong. If there is such a case, I want to know what it is.
L-P, you wrote (emphasis mine):
“You miss the point – basically you have written Monday’s business out of the protocol. Tuesday was always going to be definitive: result revealed. Monday was always going to be free of information about the toss result. The SB problem asks us to see what probabilistic conclusions, if any, she can draw from situations where Monday and Tuesday, or Before and After, are indistinguishable. Without that confusion there is no problem.”
Revealing the result of the flip on Tuesday never was part of the experiment. It is not relevant to SB’s answer, unless the reveal comes before she has to answer. And if she knows in advance that it will be revealed before she is asked (after all, she is told the full protocol of the experiment, remember?), then not being told before an answer is demanded is a sure signal that it is Monday. So if there is a reveal, it must be after she has given the answer, in which case it does not influence the answer. You are either changing the rules of the game or to intentionally confuse readers by muddying the waters with a false statement.
Then: “She knows a Tuesday bet is impossible, but she just attempts to place a bet whenever asked, and thus always succeeds in making a (Monday) bet. She never gets to place two bets in the Heads timeline.”
Being offered a bet on Monday but not Tuesday is another tip-off as to what the result of the flip was. If we want to include betting in the protocol (though it’s superfluous), the bet needs to be offered on both days, otherwise she doesn’t have the necessary ignorance for the experiment to be meaningful. The “bookmaker” in that case is the experimenter, and I am sure the cost was written into the research grant application, so you don’t need to assume the experimenter is “generous”.
Logicophilosophicus, you’re stuck in informal language, seriously, write out a formal calculation, your error has been outlined at least 5 different ways so far and your response is only to shift the language. The logic of your argument is to restate the true odds are 50-50 thus the thirders will not make their bets. If you’re going to make an informal argument, stop asserting it’s 50-50 before making your point. Derive that it’s 50-50, you haven’t done that yet.
Your analysis of her “true life odds” are from an unbiased point of view. SB is biased as we’ve already established, she has two chances to guess heads if it is heads. You seem to be under the impression that the coin determines whether she lives or dies….but that’s not quite true. In that sense her life odds are 50-50, but as long as she gets an interview as outlined in the problem, provided the flip is heads she has another chance to guess.
Let’s assume she’s not guessing optimally, i.e. guessing randomly. Following the protocol, what happens when you wake her on Monday and she guesses Tails but on Tuesday guesses Heads? Do you kill her? If she was betting, she’d take a loss on Monday but recoup her loss on Tuesday, she’d break even. If she guessed Heads on both days, then she’d gain twice. If the flip was Tails and thus she was interviewed only on Monday, then on guessing heads she’d lose once. So 50% of the time she gains twice as much as she loses the other 50% of the time. That’s 2:1 odds last I checked.
If you decide that you’re going to kill her if she guesses wrongly even once, then her life odds are 50-50, but if you allow any correct guess to save her, then her odds are 2:1. I was hoping you would derive this yourself by finally analyzing it, and I’m still giving you the chance as all of this has been informal (but logically valid). I hoped the apparent contradiction I laid out would have grabbed your interest but instead you took it literally. There are no true odds, depending on how her life is decided, it’s either halfer or thirder. Betting is always thirder though.
Questions for halfers:
1. See my earlier variation on the experiment, using boxes of iron or gold. Is your answer for this experiment 1/3? If not, then why not? If so, then what difference can you point to between this and the classic SB experiment to explain the difference in your answers?
2. See my post in which I introduced the idea of an outside witness. Should the witness assign a probability of 2/3 to heads? If not, then why not? If so, then what difference can you point to between the witness’s state of mind and SB’s state of mind to explain the difference in their answers?
3. See my post in which I calculate p(Tu|I) assuming, respectively, the halfer and thirder positions. How do you reconcile the halfer position with its implication that the probability of an interview happening on Tuesday is 0?
I do hope to hear from a halfer who is willing to engage in answering these questions. I am eager to know how such problems are resolved in the halfer world.
Thanks.
From http://en.wikipedia.org/wiki/Sleeping_Beauty_problem we have the problem:
“–Sleeping Beauty volunteers to undergo the following experiment and is told all of the following details: On Sunday she will be put to sleep. Once or twice, during the experiment, Beauty will be wakened, interviewed, and put back to sleep with an amnesia-inducing drug that makes her forget that awakening. A fair coin will be tossed to determine which experimental procedure to undertake: if the coin comes up heads, Beauty will be wakened and interviewed on Monday only. If the coin comes up tails, she will be wakened and interviewed on Monday and Tuesday. In either case, she will be wakened on Wednesday without interview and the experiment ends. Any time Sleeping Beauty is wakened and interviewed, she is asked, “What is your belief now for the proposition that the coin landed heads?”–”
If the experiment is repeated one thousand times then, on average, she will be awakened and asked about her belief fifteen hundred times during the experiments. On average, five hundred of those fifteen hundred times she is asked (i.e. one third of the times) the coin will have landed heads and so the proposition “the coin landed heads” will be true. On average, one thousand of those fifteen hundred times she is asked (i.e. two thirds of the times) the coin will have landed tails and so the proposition “the coin landed heads” will be false.
So sleeping beauty knows several facts. She knows that in repeated trials of the experiment, on average, one out of every three times she is awakened the proposition “the coin landed heads” will be true. She knows she was just awakened. So it is reasonable for her to give one third as an answer. She also knows that in repeated trials of the experiment, on average, one out of every two times that the experiment is run the proposition “the coin landed heads” will be true. She knows the experiment is being run. So it is reasonable for her to give one half as an answer. Her answer to the question should be: My belief is that, on average, the proposition is true one out of every two times the experiment is run and, on average, one out of every three times I am awakened and asked my belief about it.
L
Sean,
We could really use another post here, else everyone will keep beating this one to death. How about a list of the papers you’ve most enjoyed recently?
I just finished “From Eternity to Here”. Every page (at least once, sometimes more, despite the tiny font). Every endnote (despite the microscopic font, favorite: 273). Even a selected sampling of the bibliography (great choices, nice touch including the Buffyverse).
My arm-waving is now far more nuanced concerning entropy and black holes, thermodynamics, de Sitter / Minkowski / anti-de Sitter space, various multi-verses and baby-verses, the inflaton, and the critical importance of (and problems with) low-entropy initial conditions.
What I think I enjoyed most was your friendly conversational tone, as though you were explaining this over dinner. Next is your ability to foresee where a reader could have problems, and patiently provide ways through them, all without ever sounding condescending or rushed. I’m amazed at how little math you included, yet you still managed to communicate the “feel” in a meaningful and constructive way. Lucid and inviting.
Then I made certain my clocks were all on time. Whatever that is.
Its funny that my comment – that the sleeping beauty problem has nothing to do with quantum mechanics – got voted down. Its funny because of all the 184 comments here, not ONE of them is about quantum mechanics. Yet that was the whole point of Sean’s post; he claims he was able to solve the problem by appealing to quantum mechanics. So everyone kind of tacitly agrees with me that the problem has nothing to do with quantum, but won’t admit it.
Sorry for the length of this post.
Suppose we let SB perform the coin toss on Sunday. She catches the coin in the palm of one hand and then covers up the coin with the palm of the other hand. It doesn’t matter if she sees the result of the toss since we assume that being put to sleep erases her memory of the result. When SB is awakened according to the standard protocol, we ask her, “What’s the probability that if you uncover the coin in your hand you will see a tails?”. Now SB knows that in a large number of repetitions of the experiments, 1/3 of the time she is awakened she will be holding a tails in her hand. So, she naturally answers the question, “the probability that I will see tails if I uncover the coin is 1/3”.
Even a halfer should agree with that. But, a halfer will argue that the question we are now asking SB is not the same question as stated in Sean’s statement of the problem. In the original statement, the question asked of SB is, “What is the probability you would assign that the coin came up tails?” The halfer interprets Sean’s question as not being equivalent to the question about uncovering the coin when awakened.
A halfer might argue as follows. In one half of all experiments the result of the coin toss will be heads and in the other half of the experiments the coin will be tails. Since SB knows that she is in an experiment anytime she is awakened, she gives a 50-50 chance that the coin came up tails.
The halfer can go on and assign probabilities to the individual awakening events. But the halfer assigns these probabilities based on considering a randomly selected experiment out of a large set of repeated experiments. Let E1 and E2 denote the two awakening events that would occur following a heads and let E3 be the one awakening event that would follow a tails. In one half of the set of all experiments, E1 and E2 (but not E3) will occur sometime during the experiment. And in the other half of the set, E3 (but not E1 or E2) will occur during the experiment. So, she can say that for an experiment picked at random, E3 will have a probability of 1/2 of occurring during the experiment. (E1 and E2 will also each have a probability of 1/2 of occurring sometime during the experiment.) E3 occurs if and only if the coin came up tails, so she claims that the probability that the coin toss came up tails is 1/2.
If SB is a halfer, then when she is awakened she realizes she is in one of the events E1, E2, or E3. But she has no way to know which event she is in. Since she knows that she is in a particular experiment, she assigns a probability of 1/2 that she is in event E3. She also assigns a probability of 1/2 that she will experience both E1 and E2 in this experiment. If she is an experiment where both E1 and E2 (and not E3) occur, then she knows that when she is awakened she cannot tell if it is E1 or E2. So, she assumes a 50-50 chance of being in E1 or E2 if she is awakened in an experiment in which both E1 and E2 will occur. So, the overall probability that she would assign to being awakened in event E1, say, would be 1/2 * 1/2 = 1/4 . The first 1/2 factor is the probability of being in an experiment where events E1 and E2 will occur, and the second factor of 1/2 is the probability of being in E1 out of the set {E1, E2}. So, on any awakening, she would assign a probability of 1/4 of being in event E1. Likewise, 1/4 for E2.
If upon any awakening she is asked for the probability that the coin came up heads, she would say the answer is the sum of the probability that the current awakening is an E1 event plus the probability that the current awakening is an E2 event. Thus, the probability that the coin was heads is 1/4 + 1/4 = 1/2.
Moreover, the halfer-SB can use her probabilities to come to the same conclusion as the thirder-SB in regard to the scenario where SB holds the coin in her hand. If SB uncovers the coin in her hand every time she is awakened, the halfer will deduce that she will see tails 1/3 of the times she is awakened in a large number of repeated experiments.
Tom Snyder,
The halfer in your post is making the usual mistake in this discussion: Regarding the experiment as either Monday or Tuesday, but not both (in case of Heads). This is the only justification she has for “picking” one of these possibilities and multiply their chance by 0.5 (to arrive at 1/4).
The SB experiment has the specific property that it actually matters whether you go
–> pick experiment –> then pick one interview
or
–> pick all interviews, one by one while memory drugged
and the wording is unambiguous in that it specifies the second procedure.
A couple of further proofs that the halfer is wrong:
1) The math you give, dear halfer, fits perfectly if the experiment is EITHER Monday OR Tuesday. Do you really claim that it wouldn’t make a difference if we instead chance the experiment to BOTH Monday AND Tuesday? (All this assuming SB’s drugged point of view, as in the actual SB formulation.)
2) The simple proof that 50% must be too low for Heads is that, given Monday, the chance for Heads is 50%, given Tuesday, it’s 100%, and there is a non-zero chance it’s Tuesday. (And notice that this proof works exactly because we have BOTH. If we had either/or, the chance for Heads given Monday would only be 1/3.)
Daniel Kerr,
Your first comment way back was: “The trick is to realize there are 4 cases here, heads and Monday, tails and Monday, heads and Tuesday, tails and Tuesday. They each have 1/4 probability, but sleeping beauty only “samples” 3 of these cases, as she is not awake for tails and Tuesday. So of the 3 cases she sees, two of them are heads and if she wants to make money from betting, she’d better bet on heads.”
Let me EXACTLY paraphrase that to describe the version of Bertrand’s Box where the experimenter peeks and ALWAYS extracts a gold coin first to show the subject. (The 2 boxes we shall call H and T contain H:Gold+Gold and T:Gold+Silver.) This version is equivalent to the SB protocol.
“The trick is to realize there are 4 cases here, H and Gold(1), T and Gold, H and Gold(2), T and Silver. So of the three cases she sees, two of them are H and if she wants to make money from betting, she’d better bet on H.”
Wrong. Do you see what you’ve done? Pulling out the second gold coin IDENTIFIES the box as A – there is nothing to bet on any more; just as waking SB on Tuesday identifies the timeline as heads. This was already pointed out to you: only in a fairytale land of bookmakers who take bets after the result – i.e. not in ANY real world – does a Tuesday bet have any meaning. Reality is a zero sum game.
Well, you conjured up such a world. Instead of having to find a bookmaker, SB is to be GIVEN $1 each time she “guesses” correctly. Now you are able to say she should “guess” heads, thus winning $2 the half of the time she is right, rather than $1 if she “guessed” tails.
Wrong. Do you see what you’ve done this time? You have changed the problem so that the experimenters have a payoff of $2 set aside for CHOOSING (definitely NOT guessing or “giving credence to”) heads and only $1 for CHOOSING tails. When SB says “heads” she does not “assign probabilities” to heads and tails in the ratio 2:1; she CHOOSES the 50:50 chance with the higher payoff – the ratio 2:1 is in the payoff table, not the coint toss probabilities. The Tuesday dollar is an extra freebie.
Back in the fifth comment in this discussion, Joe Polchinski endorsed “the result 1/3 unless the additional constraint is imposed that she can only bet on Monday, which is changing the problem…” I shall EXACTLY paraphrase that to reflect the real world: The correct assignment of probability to tails, given a true coin and the stated protocol, is “1/2 unless the additional constraint is imposed that a bookmaker must take a bet on Tuesday (BUT only on heads, and after the result is published), which is changing the problem…” If the non-naturalistic element of a post-result bet is not stated in the problem, it is ridiculous to assume that the correct answer depends on importing it. (In the real world, even the withdrawal of a horse AFTER the bets are laid reduces the payoff – “Tattersall’s Rule 4” I believe. But if the withdrawal is known, there can be no bets to win on a one-horse race.)
I haven’t mentioned the induced amnesia element at all in that analysis, because it is not relevant to the odds. Consider: without amnesia, SB could bet either way on Monday with equal chances of success, while on Tuesday she is only allowed to bet if heads came up, i.e. there is no “bet”; with amnesia, she can maximise her payoff by saying “heads 2/3” because she will get access to the possible Tuesdsay freebie, plus the result of Monday’s fair bet (where heads was as good as tails anyway).
These results are not artefacts of plain language which the correct symbolism would somehow explode – the correct symbolism only works with correct inputs (GIGO). The correct symbolism is, in any case, the payoff matrix.
DN, etc,
Unless you can come up with a real-world scenario where the 2:1 assignment of probability has useful CONSEQUENCES (i.e. outperforms 50:50 in any APPLICATION) your assignment is wrong. The proof of the pudding.
Whoops. I omitted the paraphrase of this sentence:
“They each have 1/4 probability, but sleeping beauty only ‘samples’ 3 of these cases, as she is not awake for tails and Tuesday.”
becomes:
“They each have 1/4 probability, but sleeping beauty only ‘samples’ 3 of these cases as the experimenter is committed to showing the Gold coin, i.e. disallowed from revealing the Silver, when box T has been selected.”
Logicophilosophicus, my patience grows thin for reading informal arguments. Many mathematical calculations have been provided in these comments and result in the thirder result. My informal explanations are interpreting these calculations, they are not arguments in themselves. So as you attack my attempts to translate mathematical truth into informal language to convey understanding, you’re not attacking the argument at all. Ultimately your argument lies in showing how the calculation is in error. I have yet to see that and as such my interest in and ability to be persuaded by your arguments is rapidly diminishing.
I will just say, in your analysis above, you clearly reject the notion of a conditional probability. You don’t understand that the pay-off is a result of a probability weight and is completely compatible with the coin odds being 50-50. Of course she goes with the 50% chance that has a higher payoff and that’s because she gets to bet twice. Your analysis seems to omit that if she guesses randomly the extra payoff is not free. The extra payoff is received only if she guesses correctly both times for a coin flip of heads.
And arguments like this are not satisfactory:
“Wrong. Do you see what you’ve done? Pulling out the second gold coin IDENTIFIES the box as A – there is nothing to bet on any more; just as waking SB on Tuesday identifies the timeline as heads. This was already pointed out to you: only in a fairytale land of bookmakers who take bets after the result – i.e. not in ANY real world – does a Tuesday bet have any meaning. Reality is a zero sum game.”
First of all, your analogy doesn’t hold as in the original SB she can’t remember previous interviews. The second gold is tantamount to her having the knowledge that it’s Tuesday. You said yourself this is irrelevant to the problem, I don’t understand why you would choose an analogy that makes it absolutely integral to her state of knowledge and one where the analogy doesn’t hold as she has to know that it’s indeed Tuesday/Gold(2).
The correct analogy is to say that she has no memory of the coin she has already drew and she doesn’t know how many coins are still left in the box, then it’s described by the same mathematical calculation you have yet to address.
Daniel Kerr,
“…she goes with the 50% chance that has a higher payoff and that’s because she gets to bet twice. Your analysis seems to omit that if she guesses randomly the extra payoff is not free. The extra payoff is received only if she guesses correctly both times for a coin flip of heads.”
If she gets to bet twice then “the additional constraint is imposed that a bookmaker must take a bet on Tuesday… after the result is published” which is a non-naturalistic condidition. She does not get to bet twice unless you impose that strange condition. Money may not be as important as life itself, but this is just as strange as the idea you suggested earlier, that if she had two lives to lose etc etc.
Please clarify “not free” – where does the extra dollar come from? A bookmaker prepared to take a bet on a one-horse race? Or is it built into the known protocol? Let me put this differently. Suppose the protocol includes this sentence: “Your assignment of a probability is taken to mean that you would be as happy to place as not to place a bet on that result (H or T) at those odds against that result on the universal understanding that a bet is only acceptable before the result is published.”
You say my box analogy is inappropriate because she would have to be unaware whether a coin had already been shown. No. The indistinguishability of Monday and Tuesday is analogous to the indistinguishability of the coins. G(1) does not mean “the first gold coin to be taken from the box”: it is the identity of the coin (e.g., if you like, a microscopic number scratched into its surface). The temporal distinction between M and T, concealed by induced amnesia, is fully analogous to the physical distinction between G(1) and G(2), concealed by perfect similarity of manufacture.
GIGO refers to the fact that your calculation may be impeccable – I haven’t checked – but since there is some “garbage in” there is necessarily “garbage out”.
[edit: I missed a point. You wrote that “the second gold is tantamount to her having knowledge that it is Tuesday” – but the point is that that “the second gold is fully analogous to the fact that on Tuesday EVERYONE ELSE knows that it is Tuesday, that the result is heads, that no bet can be placed.” SB knows that on ONE of her awakenings in a heads-timeline no bet is possible, and she factors that knowledge into her assignment.]
L-P,
You wrote:
“Back in the fifth comment in this discussion, Joe Polchinski endorsed “the result 1/3 unless the additional constraint is imposed that she can only bet on Monday, which is changing the problem…” I shall EXACTLY paraphrase that to reflect the real world: The correct assignment of probability to tails, given a true coin and the stated protocol, is “1/2 unless the additional constraint is imposed that a bookmaker must take a bet on Tuesday (BUT only on heads, and after the result is published), which is changing the problem…””
You are misapplying Joe’s statement. Joe correctly said that adding a constraint that bets are only accepted on Monday is “changing the problem”. The original problem does not have the constraint. So when you start with that constraint in place (to get a probability of 1/2), and remove it to allow SB to place a bet on Tuesday if she is awake, then the result of 1/3 isn’t from “changing the problem”, it is from returning to the problem as originally formulated.
You are persistent in artificially requiring that the only bookmaker that SB is allowed to place a bet with must be one who is both (a) in possession of inside information that SB does not have and (b) motivated to maximize profit. Of course, SB would not accept a bet at 2:1 odds from such a bookmaker, if she knows the bookmaker fits this description. That is because knowing that the bookmaker is offering the bet at all tips SB off to the fact that it is Monday, with the result that she now should not accept the bet because it is not a fair bet. But that is not the state of her knowledge at the time the interview takes place in the original experiment.
I already gave two examples of fair bookmakers – one who fails to meet condition (a) and one who fails to meet condition (b). Any representation of SB’s assignment of probability by way of fair betting odds needs to assume a fair bookmaker, not one using inside information to serve a profit motive.
I went back to find your gold coin argument. It is indeed analogous to the SB problem, but it also fails to support the halfer position. Once you formalize the probabilities, it is easy to see why.
H = heads
T = tails
Au = the evidence of seeing a gold coin
Au1 = this instance is the first instance of seeing a gold coin
Au2 = this instance is the second instance of seeing a gold coin
The “1” and “2” indices are hidden variables from SB’s point of view, but she understands that
p(H|Au) = p(H|Au1) * p(Au1|Au) + p(H|Au2) * p(Au2|Au)
p(T|Au) = p(T|Au1) * p(Au1|Au) + p(T|Au2) * p(Au2|Au)
Noting that:
p(H|Au1) = 0.5
p(T|Au1) = 0.5
p(H|Au2) = 1.0
p(T|Au2) = 0.0
leads to this:
p(H|Au) = 0.5 * p(Au1|Au) + 1.0 * p(Au2|Au)
p(T|Au) = 0.5 * p(Au1|Au) + 0.0 * p(Au2|Au)
The second equation shows that p(Au1|Au) = 2 * p(T|Au), so substitution into the first equation gives:
p(H|Au) = p(T|Au) + p(Au2|Au)
Conditional probabilities (like other probabilities) cannot be negative. This means that either the second gold coin can never be shown (p(Au2|Au) = 0), or p(H|Au) is greater than p(T|Au). But in the case of heads, the second gold coin is required to be shown, so p(Au2|Au) is greater than zero, and the halfer position that p(H|Au) = p(T|Au) is disproven.
Logicophilosophicus, as I said before, my patience ran thin. Your argument against the betting analogy is that a bookmaker wouldn’t take a bet for an event that has not yet transpired. This is a non sequitur and I really have no response to that. You say there’s garbage in, and I’ve asked you multiple times to correct my probability assignments, and you haven’t yet. Instead you resort to poorly formed analogies to make your points. Perhaps this works in some circles, but I like logic and frankly, analogies explicitly don’t necessarily preserve logical invariance, so you’re not making an argument.
p(H|I) seems to be the probability of getting a heads result given that an interview has already taken place. How does the protocol allow that sequence? There’s more that a hint of time travel there. Using normal Games Theory practice, I would draw a tree diagram and base any strategy on probabilities based on total enumeration. In this really simple scenario we have just two branches,
H->I->I->?
and
T->I->?
To reason backwards in time is a little odd, but just because SB can’t tell the difference between these three actually quite distinct interviews cannot make the I in the second branch lead back to an H in the first branch (we can’t jump from one branch to another); nor especially can it make the two I’s in the first branch lead back to two H’s, creating a third branch out of nowhere. Reasoning back in time from, say, the second I in the Heads branch leads back through the first I to the single H.
There was an old Bhutanese Sherpa who spent his summers escorting climbers from the tourist centre T to the hill camp H. The tourists arrived by plane on the Saturday, were driven as far as possible to T, and on Sunday morning began the arduous trek to H, which they reached on Tuesday evening. The old BS would accompany returning climbers from H to T, which was just as hard terrain, but took a day less. Often he would wake, still exhausted and confused, and wonder for a moment whether he was half way down, or a third of the way up, or two thirds of the way up. But he never once reasoned that in the long run he would end up at H twice as often as T…
Richard,
“I went back to find your gold coin argument. It is indeed analogous to the SB problem, but it also fails to support the halfer position. Once you formalize the probabilities, it is easy to see why…
Au1 = this instance is the first instance of seeing a gold coin
Au2 = this instance is the second instance of seeing a gold coin”
Well I went back to my argument because I was sure I deliberately and explicitly said something entirely different…
“G(1) does not mean ‘the first gold coin to be taken from the box’: it is the identity of the coin (e.g., if you like, a microscopic number scratched into its surface). The temporal distinction between M and T, concealed by induced amnesia, is fully analogous to the physical distinction between G(1) and G(2), concealed by perfect similarity of manufacture.”
Daniel Kerr,
“Logicophilosophicus, as I said before, my patience ran thin. Your argument against the betting analogy is that a bookmaker wouldn’t take a bet for an event that has NOT YET transpired. This is a non sequitur and I really have no response to that.”
I believe I actually asserted the very opposite:
“But what you have totally failed to take into account is that SB’s induced confusion over the day – Monday or Tuesday – is entirely confined to SB’s mind. If you can find me a bookmaker so improbably generous as to take a bet on the winner AFTER the stewards have ruled on the photofinish, I’ll get rich, too.”
As I indicated in my reply to Richard, I thought I did have an understanding of conditional probability: p(I|H) is the probability of an interview, given that the result was (i.e. in the past) heads. I think p(I|T)=1, and p(I|H)=1. What is your understanding? And what does p(H|I) imply?
(BTW, just a quibble: The statement about when a bet can be accepted is just, as I stated, a “universal understanding”. I didn’t deduce it, illogically or otherwise, from other propositions, so whatever else it is, it cannot be a “non sequitur”. If you actually “like logic”, that is an odd mistake to make. Well, universal except for one or two people here. That was EXACTLY the thrust of my “What is an a posteriori probability?” remark.)
As several commentators have said, this post and the discussion here essentially deals with intriguing classical probabilities, not quantum theory. If we return to quantum theory and the Everett proposal as in the last post, the key statement there is:
“Like the textbook formulation, Everettian quantum mechanics also comes with a list of postulates. Here it is:
1. Quantum states are represented by wave functions, which are vectors in a mathematical space called Hilbert space.
2. Wave functions evolve in time according to the Schrödinger equation.”
But that is *not* what happens in the steps set out in the inset calculation later in that post. There are four steps in that process. I leave out the common factor of (1/ \sqrt{2}), which makes no difference, and give both the written description of the process, and the short summary given in the diagram (square brackets)
1. Everything is in its starting state, before the measurement:
Observer: |O_o>, electron: (|up> + |dn>), Apparatus: |A_o>, environment:|e_o> .
2. The apparatus interacts with the system to be observed and becomes entangled. (“Pre-measurement.”) [Apparatus measures]:
|O_o> (|up> + |dn>) |A_o>|e_o> -> |O_o> (|up>|A_up> + |dn>|A_dn>) |e_o> ) (1)
3. The apparatus becomes entangled with the environment, branching the wave function. (“Decoherence.”) [Decoheres]:
|O_o> (|up>|A_up> + |dn>A_dn>) |e_o> -> |O_o> (|up>|A_up>|e_up>| + |dn>|A_dn>| e_dn>) (2)
4. [Self -locating uncertainty]:
|O_o>(|up>|A_up>|e_up>| + |dn>|A_dn>| e_dn> ) = |O_o>|up>|A_up>|e_up> + |O_o>|dn>|A_dn>| e_dn> (3)
5. The observer reads off the result of the measurement from the apparatus. [Measurement complete]:
|O_o>|up>|A_up>|e_up> + |O_o>|dn>|A_dn>| e_dn> -> |O_up>|up>|A_up>|e_up> + |O_dn>|dn>|A_dn>| e_dn> (4)
The overall process is thus
|O_o> (|up> + |dn>) |Ao>|eo> -> |O_up>|up>|A_up>|e_up> + |O_dn>|dn>|A_dn>| e_dn> (5)
and so the wave function has split into the two possible options (with equal weights).
Now the intriguing point is that, despite statement 2. above, at no point in this set of steps is the Schrodinger equation used. On the contrary, this process involves a series of three irreversible, hence non-unitary, projections.
Take step (1). By the linearity of quantum theory (|up> + |dn>) |A_o> = (|up> |A_o>+ |dn>|A_o>), so the essential dynamics is
(|up> |A_o>+ |dn>|A_o>) -> (|up>|A_up> + |dn>|A_dn>) (6)
This is in fact double non-unitary projection, each projection occurring with numerical factor unity, so representing equal probabilities of these two projections:
|A_o> -> |A_up>, |A_o> -> |A_dn>. (7)
This is irreversible (and hence non-unitary) because you can’t determine the initial state |A_o> from the final states |A_up> and |A_dn>. The information needed to determine |A_o> simply isn’t there at the end. Essentially the same happens at stages (2), which is irreversible projection of |e_o>, and stage (4), which is irreversible projection of |O_o>. Stage (3) does not involve projection and does not have to be inferred by means of some philosophical assumption (“Self -locating uncertainty”): it just follows straightforwardly from the linearity of quantum theory.
Now one might try to follow the decoherence route and say, things are in fact unitary, so while there are indeed other terms in these equations, they are not shown because they are so incredibly small that we can neglect them and effectively get the progression above by use of the Schrödinger equation alone, even though the dynamics (1)- (4) is non-unitary. There are extra very small terms in these equations that have been deleted because they are of no consequence.
But it is precisely that step of deleting these very small terms that makes the whole dynamics irreversible and hence non unitary. This is essentially the same as in the case of the claim that if we could reverse precisely the velocities of every atom in a broken wine glass and its surroundings after it has fallen on the floor, it would jump back up and reassemble on the table to reform the pristine object. This reversal is theoretically possible, even if not remotely practicable, because the underlying dynamics is Hamiltonian. However if you neglect these incredibly small velocities of the remnants and their surroundings and set them to precisely zero, that theoretical option is no longer available. But that is what the above progression amounts to.
In summary: the dynamic progression (5) does not follow from assumptions 1. and 2., as claimed. It has extra assumptions which in effect amount to wave function collapse (see (6) and (7)).
Sorry, I did not have the courage to read all comments, so this has probably been said many times before. Nonetheless, why do so many again and again let themselves be fooled by playing the silly wordgames philosophers are so renowned for.
The answer to the question “What is the probability you would assign that the coin came up tails?”” is of course 1/2.
The answer 1/3 is the correct answer to three totally different questions:
1)” What is the probability that you are now being interviewed on a monday and won’t be interviewed again on tuesday?”
2) “What is the probability that you are now being interviewed on a monday and will be interviewed again on tuesday?”
3° “What is the probability that you are now being interviewed on a tuesday?”
And of course, the answer to the question “What is the probability that you are now being interviewed on a monday” would have to be 2/3.
The fact of being interviewed on a particular day does not influence the outcome of tossing a coin one or two days before. Causality.
Johan,
You write:
No, but the fact that you are being interviewed may certainly influence your credence in the outcome of the tossed coin, particularly when said fact depends on the outcome of said toss.
Consider the extreme revision where you are not interviewed at all after heads. Then your credence in heads is 0% if/when interviewed.
DN writes “No, but the fact that you are being interviewed may certainly influence your credence in the outcome of the tossed coin, particularly when said fact depends on the outcome of said toss.”
OK, in that case I would call it a “mind game”.
Suppose (when heads) you don’t wake up SB two times in identical circumstances, but instead three times, four times, etc. … ad infinitum?
The “credence” as you call it of coming up tails would go from 1/3 to 1/4 to … in the limit zero.
From a “psychological” point of view I can understand why SB would want to believe that (and fairy tale figures have the advantage of living forever), but in that case I would call it misleading to refer to probability (theory).
As for the connection with the Many Worlds Interpretation and Multiverses, it’s always tempting to get human consciousness involved, but that’s a can of worms I’m not going to open.