Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
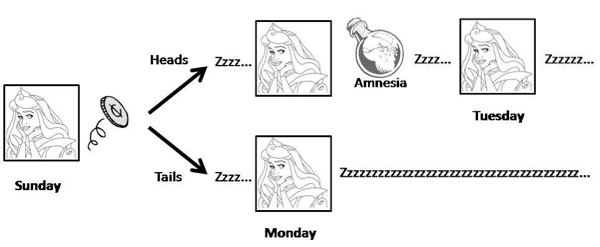
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
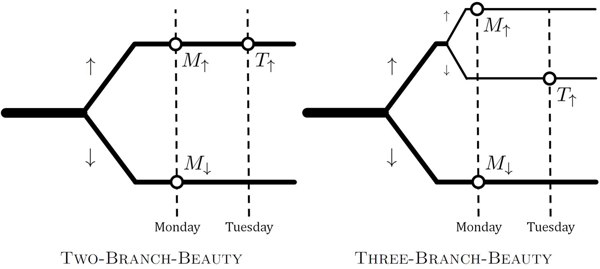
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
Here’s another example that demonstrates that the “no new information” argument is flawed.
1. If tails, 50% chance of an awakening.
2. If heads, 100% chance of an awakening.
3. If SB is not awakened, we let her sleep and start over the next week with a new coin flip. We carry on until SB is awakened. (SB knows this.)
The first two rules alone give a 1/3 tails chance. And I submit that they also give a 1/3 tails chance when rule 3 is added. These rules have been specifically chosen for making this 1/3 claim “obvious” and hopefully easy to agree with.
However, halfers can argue that when awakened under just the first two rules alone, she gets new info about the outcome of the 50% flip after tails, so it’s “ok” that she now has 1/3 credence rather than 1/2.
However, with the addition of rule 3 in the protocol, SB knows that she will be awakened 100% of the time after experiment start. Hence, “she gets no new information” according to the standard halfer argument.
So either:
A) The halfer must insist on also 1/2 tails credence under this 3-point protocol, or
B) The “no new information” argument must be flawed (or for some reason only apply in the original SB protocol and not in this 3-point protocol).
I think the choice is pretty easy. And we have seen many others point out that “I will be awake (under such and such conditions)” is just not the same (as much) information as “I am awake right now (under such and such conditions)”.
I gave another absurd example here:
https://www.preposterousuniverse.com/blog/2014/07/28/quantum-sleeping-beauty-and-the-multiverse/#comment-7295910552604296023
[Logicophilosophicus, it seems we are not really addressing each other’s arguments, so I agree to disagree.]
Logicophilosophicus, since you’re not using probability theory to frame your arguments, I am having a hard time following your reasoning here. For your analysis to hold, it seems to me that SB cannot know P(Wake|Day) for any day, for if she did that would the information in itself. So phrased another way, you’re assuming SB is daft and doesn’t know the setup of the experiment, yet according to the problem statement she is clearly aware of the setup. The calculation that results in 1/3 probability for heads is not a mistake, it’s derived given SB’s knowledge of P(Wake|Day), which you seem to be contesting that she should know that.
D Kerr et al,
Well I guess that makes me daft, since it is my reasoning I project onto the hypothetical SB.
A coin is tossed. A result slip is printed reading “RESULT HEADS” or “RESULT TAILS”. This is explained to a statistico-psychological guinea pig, as is the fact that he will be hypnotized to forget his first update in the Heads scenario.
The update consists of a statement by the experimenter: “There is at least one letter E on this results slip.” In the case of heads, he will be told twice, but cannot know whether this has happened yet, of course.
If the experimenter had to stick a pin at random in the text, and chanced upon an E, the thirder conclusion would be correct. But the experimenter was mandated to make the E statement, therefore no new information.
The remarkable conclusion of the SB-thirders is that the constraint (only an E statement allowed/mandated) is devoid of statistical information, since they still come up with 1/3. Actually it is an astounding conclusion. The Monty Hall problem hinges entirely on the fact that Hall is constrained – replacing the constraint with random selection by MH leads to a thirder solution; adding the constraint leads to a halfer solution.
In any other probability problem a key issue is random vs non-random, and it is always a game changer. What is different about SB? (I’ll suggest an answer to my own question: SB-thirders seem to think that the two wakings in the heads timeline and the single waking in the tails timeline are not only psychologically indistinguishable, but are [therefore???] of equal probability 1/3 – rather than the more justifiable 1/4, 1/4 and 1/2 – and are all simultaneously available for random selection like some kind of Three Card Monte.)
Logicophilosophicus,
You write:
Well, not quite. The calculation is like this:
Number of interviews pr. trial: 1.5
Number of tails interviews pr. trial: 0.5
Ratio: 0.5 / 1.5 = 1/3
If the coin had been 70/30 tails-heads, the math would have been 1.3 in total, 0.7 tails, and 7/13 chance of it being a tails interview.
Strangely enough, I find myself saying that the best answer is P=0. This is clearly the answer when a cumulative reward is offered, say $1 per correct answer, and the purpose is to maximise the payoff.
Halfer:
0.5(0.5+0.5) + 0.5(0.5)=3/4
Thirder:
o.5(2/3+2/3) + 0.5(1/3) = 5/6
Zeroer:
o.5(1+1) + 0.5(0) = 1
These are in units of ‘long-term average dollars’, with P=0 giving the maximum return. When thinking about halfer and thirder positions, I can’t help but take the phenomenalist’s stance and wonder what the point is, from Sleeping Beauty’s point of view? What is she supposed to do with P=1/3? It won’t maximise her number of correct responses, for example.
Halfers and thirders disagree on “how to assign” an interview to the SB, or how to account for all the interviews.
Halfers want to split along the coin flip. Thirders counter that you then effectively change the rules of the game to be only one interview on each outcome, rather than 2 interviews after heads.
Thirders want to lump all interviews together. Halfers counter that either tails or heads happen, but never both simultaneously, so we have to split up along the coin flip.
Below, I will present a new way to argue for the correctness of the thirder lump together frequency approach. It is written to help convince any halfer doubter who might be willing to be convinced.
We first look at a game with obvious odds 1/3, and we then tweak back to the SB game in such a way that the “lump together” frequency approach should still be seen to be ok.
—- Zero or one interview pr. day, interviews Monday, Tuesday and Wednesday.
—- The Monday interview is red, the other two are blue. (Imagine the interviewer holding a red or blue ball behind his back.)
—- SB is memory drugged after each day, she knows the rules.
*** 1 ***
A coin is tossed.
If tails, none of the interviews will take place.
If heads, all the interviews will take place.
Upon being awakened, what is SB’s credence that it is a red interview?
*** 2 ***
A coin is tossed each day (so 3 flips in total) to decide if that day’s interview will take place.
Upon being awakened, what is SB’s credence that it is a red interview?
*** 3 ***
A coin is tossed to decide for the red interview, another coin is tossed to decide for the blue interviews (both or none take place).
Upon being awakened, what is SB’s credence that it is a red interview?
*** 4 ***
A coin is tossed.
If tails, the red interview takes place.
If heads, the blue interviews take place.
Upon being awakened, what is SB’s credence that it is a red interview?
As you may notice, case 4 is just like case 1, except the red interview is “switched” so that it takes place after tails rather than after heads.
Also, you may notice that case 4 and case 1 are just like case 3, except case 3 may, or may not, align the red interview with the blue interviews.
In case 2, we really don’t know the number of interviews to take place at trial start. It could be 0, 1, 2, or 3.
Anyway, the math is still simple:
Number of blue interviews pr. trial: 0.5*1 + 0.5*1 = 1
Number of red interviews pr. trial: 0.5*1 = 0.5
Interviews pr. trial: 1 + 0.5 = 1.5
Red interview chance: 0.5 / 1.5 = 1/3
The math is exactly the same in all 4 cases (nitpicking; you may want to put some brackets when a toss aligns several interviews, but the results are the same).
To make the final conclusion, note that in case 4, we have:
credence it is a red interview = credence it is a tails interview
br,
Suppose SB is offered this share when interviewed:
Then the fair price for that share is 33$. If she pays more, she will lose money, if she were to offer less, she would be outbid by another guy who would still make a profit. But 33$ breaks even.
The fair price for a share on a given outcome is a pretty accepted way to define the probability of that outcome.
DN says:
“Below, I will present a new way to argue for the correctness of the thirder lump together frequency approach.”
Thank you for that, but I would like to ask what a credence of 1/3 really means, from her point of view. Does it mean, for example, that if you also asked her the question “guess which side is up of the coin I’m holding?”, she would answer, on average, tails once and heads twice, for every three times asked. Is that correct? If so, it would lose to the position where she always answers heads, if one is counting the number of correct replies (or dollars) over a large number of trials. Hence I don’t see P=1/3 as useful for anything, and if it has no consequence then she may as well say P=1/2!
DN:
“This share will pay 100$ if the coin flip was tails
Then the fair price for that share is 33$.”
Seems we cross-posted. OK, I accept this is the fair price. Hence I accept that one gets different answers depending on how one rephrases the question!
Still, I feel that my approach has significance, because if she has to guess ‘heads’ or ‘tails’, then the winning strategy is to guess ‘heads’ at 100%.
DN,
Me: “SB-thirders seem to think that the two wakings in the heads timeline and the single waking in the tails timeline are not only psychologically indistinguishable, but are [therefore???] of equal probability 1/3 – … – and are all simultaneously available for random selection like some kind of Three Card Monte.”
You: “Well, not quite. The calculation is like this:
Number of interviews pr. trial: 1.5
Number of tails interviews pr. trial: 0.5
Ratio: 0.5 / 1.5 = 1/3”
To quote Catch-22, “I may be stupid, because the distinction escapes me…”
Well, if she knew in advance about the plan, than the probability of her waking up on Monday would be 1/2. That is always the case. The question is what happens when she wakes up Tuesday and told it was Tuesday. Since there were two possible outcomes for Monday we could say that the wave amplitude was two. So when one of those events is realized the possibility for the next event would be four satisfying the Born rule 1/2 x 1/2 equals 1/4. However, if she is told it is Tuesday, she knows that one of those possibilities did not realize, in other words she has a clear view of the past which has allowed her to eliminate one possibility. So by knowing that a specific event is required in order to satisfy a condition for her observation the Born rule is broken, and by my reckoning that leads to a finite number of possibilities that is reduced on successive observations.
Logicophilosophicus,
OK then, here we agree on what the reasoning is (even if you may not agree with it). I just like to point out that part of why is it 1/3 is that it is a fair coin. Otherwise the different awakenings would not be equally likely.
In other words: They are not equally likely (only) because they are indistinguishable, but because they are “produced” equally often (+ are indistinguishable).
Logicophilosophicus, I urge you to write down your calculations like I did in my first comment, things are a lot more apparent when you actually compute the problem. You are describing things only in an informal language and the meaning is getting lost because the syntax of English does not preserve logical correspondence. You’ve replaced the waking event with this statement regarding the letter “E,” but not just that, you’ve also replaced the day structure. You’ve changed the underlying probability space, this is not an analogy.
In the previous problem there was a distinction between the probability state of “wake” and “day.” You’ve obliterated this distinction and combined them under the letter “E.” As a result, tails and being told the statement twice has de facto a probability of 0. This analysis is already different from the Sleeping Beauty problem. Your probability space has only 2 outcomes, heads and E twice; tails and E once. The guinea pig still has a sample space of 3 due to having no memory, but two of the samples are coupled and are really only one sample together. The probabilities are different for GP as compared with SB since there are only 2 outcomes and not 4 as in the original problem.
You take issue with the original problem as you think the probability assignments should be 1/2, 1/4, 1/4, but you have no justification for this except for this invalid analogy. I’ll tell you my probability assignments and I’ll justify them. Heads and Monday, 1/4; Tails and Monday, 1/4; Heads and Tuesday, 1/4; Tails and Tuesday, 1/4. There are 2 random variables here rather than 1 as in your analogy. The day is a variable in addition to the coin flip. Each are mutually exclusive and the two are independent, so each outcome MUST have an equal probability, leading to the 1/4 assignments above. SB samples only 3 of them, much like your analogy, but she uniquely samples 3 of the 4, hence getting the thirder result.
SB’s knowledge of the days of the week completely inform her probability assignments. She knows that the interviews are conditioned on the days as well, which gives her more information about how to assign her conditional probabilities. GP has no such knowledge and thus cannot incorporate such information in its calculation. For GP, the experimenters are not conditioning their actions on a second random variable, everything is determined by the coin flip uniquely, hence GP sees an equal probability for the flip no matter how many times GP is asked on heads.
In pseudo-code, you have the following structures:
GP:
If coin = H: Ask result, Ask result
If coin = T: Ask result
SB:
Coin flip = random_uniform [H,T]
For Day = [Monday, Tuesday]:
-If Day=Monday: Ask result
-If Day=Tuesday & Coin flip = H: Ask result
If we then wrote a program to optimize the value to assign result to be right most of the time, the answers for these two problems would be different.
I should add that in both cases (GP and SB), if we were to catalog a table of the correct answers for each time GP or SB is asked, we will get a table where 2/3rds of the entries will be heads. Thus when we are asked to guess an entry in the table, naively we would expect to guess heads.
However, by your argument you say that not every entry is equal, the probability of being asked for each entry in the table is not equal. You would say that any two heads combined have an equal probability being asked for as any single tails. My pseudocode for GP does not reflect this, probably because it’s fallacious reasoning. Ultimately we’re asking to guess an entry in the table described above, since we do not know if we’re double guessing or not, we should assume we are to maximize our result. If we guess heads 100% of the time, we will be right 2/3rds of the time.
So you can ignore my argument about the days of the week/second random variable. Those help to stratify the probability space and clarify the analysis, but the result holds regardless.
But I think the point being made here is that if there is consciousness, i.e. if sleeping beauty is awake, one of the possibilities must be eliminated. If on Monday the coin is flipped and sleeping beauty never wakes up there isn’t another coin flip. We may even say that the definition of consciousness is that she realizes there was a possibility she would never wake up, namely the addition of the set containing zero elements. In the case where there were two possibilities heads or tails, the chance is one out of two. But if me or sleeping beauty is thinking about the possibilities one of the chances had to have been eliminated by adding the set of zero elements. Therefore in the “thirder view” introducing consciousness reduces one element of the probable outcomes. And this is a very crucial point because although the universe is composed of magnitudes which behave in accordance with the rules which govern magnitudes, namely mathematics, these magnitudes are really only approximations which constrains an observer who views outcomes as the result of strictly math wrong on certain occasions.
D Kerr,
I shall give my informal calculation based on a biased coin, which lands tails 51% of the time. No doubt if I wrote it in the form P(x|y) or used Born’s rule it would work out differently – you can put me right.
Remember, the protocol is that if the coin comes up heads, SB will be woken-and-asked, memory-wiped, woken-and-asked; if tails, just woken and asked. Calendars and other clues are not permitted. SB is aware that tails are favoured 51:49 a priori.
Not being as daft as I am, she will bet that the coin came up heads when she is woken and asked. In the new protocol she is asked to bet HER LIFE on the result she selects – I expect she would be well advised to go with the best estimate of the probability.
And, unsurprisingly, 51% of the time the smart SB-thirders end up dead. Meanwhile the daft halfers get it right.
DN,
I don’t think the percentage matters (the difference between your cases 2C and 4C).
They don’t matter to a thirder. They shouldn’t matter to a halfer. If the probability of producing bags is upped from 10% to 99.99%, why should that 0.01% chance of “no bags” affect the halfer’s conclusion?
What I really want to know is: What does a halfer make of the experiment I proposed? And, if the halfer agrees that the probability of gold is 1/3, what does the halfer think is the key difference (from SB’s epistemic point of view) between my experiment and the original SB experiment?
Here is a another variation: On each day of the experiment on which an interview is conducted, a person on the street is selected at random (without replacement, to ensure the same person is not selected twice in the case of heads) to witness the interview. This person is told all the details of the experiment, except the result of the toss and whether it is the first or second day that SB is awakened. What credence should the outside witness give to the proposition that “the toss was heads”?
Assuming that halfers give a different answer for the outside witness than they give for SB, what information does the witness have that SB does not?
* Neither knows the result of the toss.
* Neither knows which day of the experiment it is.
* Both know the experimental protocol.
Logicophilosophicus, I realized phrasing my argument in terms of the calendar is misleading, the second random variable manifests as a second question, the structure of the days do not matter. However you still have evaded to provide a justification or calculation. Since this does not seem forthcoming, I suggest you take the perspective of the table I outlined above as I think we can both follow it easily.
We do agree that such a table for 50-50 odds would have 2/3rds of its entries as heads, do we not? For every time the coin is heads, two entries in the table are heads too. So your argument comes down to justifying that when SB is asked to guess a random entry of the table, why she should treat each entry has having different probabilities of being asked. Since she has no memory of each interview, she has no basis for assigning the entries of the table different weights. If she guesses heads every time, then in the cases where she’s interviewed twice, she will be right and in the cases where she’s interviewed once, she’ll be wrong. Thus 2/3rds of the table will be filled out correctly by SB, yet 1/2 of the time the result will be heads. The two are not in conflict. If her life was bet on it, 1/2 of the time she would live if guessing heads but be right 2/3rds of the time.
The information SB has is that she has a 1/2 probability of being asked the same question twice, but only if the result was heads. If each question corresponded to its own coin flip even if a second coin flip was only done if the previous result was heads, the probability would then be 1/2. But anytime she’s being asked a question, there’s a chance it’s the same question yet again, so that’s information she has about the problem is independent of the calendar days. The calendar days in my above analysis substituted for this knowledge, but in general the days do not need to be referenced.
Daniel Kerr,
Right but DEAD? I suppose she can have the table engraved on her tombstone.
P(alive) = 49%, P(dead) = 51% and the thirders lose. No argument.
Logicophilosophicus,
No matter what she decides the best betting strategy is, her credence is still 2/3 heads, 1/3 tails (slightly modified by your loaded coin). But you can’t expect her to bet according to her credence under the terms you gave. In particular, she places only one bet (repeating the same bet on Tuesday doesn’t count if she only has one life to lose).
Note, if she did have two lives to lose, she should bet on heads. If she’s right, she still has both lives after Tuesday. If she is wrong, she still has one life left.
H = heads
T = tails
M = Monday
Tu = Tuesday
I = the evidence of being awake and interviewed
p(H|I) = p(H|MI) * p(M|I) + p(H|TuI) * p(Tu|I)
p(T|I) = p(T|MI) * p(M|I) + p(T|TuI) * p(Tu|I)
If SB is informed at the start of the interview that it is Monday, then she should assign 0.5 to the probabilities of heads and tails:
p(H|MI) = 0.5
p(T|MI) = 0.5
If SB is informed at the start of the interview that it is Tuesday, then she should assign:
p(H|TuI) = 1.0
p(T|TuI) = 0.0
So,
p(H|I) = 0.5 * p(M|I) + 1.0 * p(Tu|I)
p(T|I) = 0.5 * p(M|I) + 0.0 * p(Tu|I)
Halfer position:
p(H|I) = p(T|I), which means the solution to the simultaneous equations requires 0 = p(Tu|I). The halfer position is valid only if there is to be no interview conducted on Tuesday, regardless of the toss.
That doesn’t match the problem statement. Let’s try the thirder position:
p(H|I) – p(T|I) = 1/3 = p(Tu|I)
p(M|I) = 2/3
That’s better: If SB is being interviewed, it’s more likely to be a Monday than a Tuesday, but Tuesday can’t be ruled out.
Logicophilosophicus, with a name like that I thought you’d be interested in pursuing how her guess odds are 2/3rds but her life odds are 1/2. Both are true. However from her perspective, her life odds are 2/3rds guessing heads, provided she’s killed only after the whole process and not immediately after the interview.
Also thanks Richard, for having a much more succinct calculation above unlike my first comment’s misreading of the problem!
You cover your eyes and flip a fair coin. The coin lands. Without looking, what is the probability that it is heads? 50%. Now assume you look and it is heads. What is the probability it is heads? 100%. Halfers, who refuse to accept that the new information changes the probability from the perspective of the person receiving the new information, would incorrectly say still 50%.
hubdog, it isn’t that halfers refuse to believe that new information changes the probability. The problem is that they don’t recognize that the informational context of the interview is different from that at the beginning of the experiment, in the first place. In other words, they think p(H|I) = p(H) because they don’t see the interview “I” as being informative.
But SB is giving p(H) = 0.5 at the start of the experiment (Sunday night) because she isn’t being asked in the context of an interview. When asked during the interview, she must give p(H|I) which is a different thing. If she wants to calculate it in long form she can do it according to my previous post above: p(H|I) = p(H|MI) * p(M|I) + p(H|TuI) * p(Tu|I). For that she needs:
p(H|MI) = probability toss was heads if this is a Monday interview = 0.5
p(M|I) = probability that this is Monday if SB is being interviewed = 2/3
p(H|TuI) = probability toss was heads if this is a Tuesday interview = 1.0
p(Tu|I) = probability that this is Tuesday if SB is being interviewed = 1/3
This is clearly different from the context of Sunday night. On Sunday, she knows p(H) = p(HSu) = p(H|Su) * p(Su) = 0.5 * 1.0 = 0.5.
The knowledge (on Monday or Tuesday) that she is experiencing an interview prescribed by the experimental protocol replaces the full knowledge of what day it is, which was lost when she was put to sleep on Sunday night. Losing information also changes the informational context, and so changes her credence. (She can restore her original 50/50 credence by learning that it is Monday, or increase her credence to 100% by learning that it is Tuesday — but neither of these bits of information is relevant on Sunday.)
Richard, Daniel Kerr,
“…her guess odds are 2/3rds but her life odds are 1/2. Both are true.” But she already KNEW those true “life odds” at the original briefing on the protocol. She cannot rationally know one set of odds to be true and crucial, and yet deny them.
The idea “if she had two lives to bet” is crazy, but let’s follow it through. You claim that by killing SB I have unfairly truncated the experiment, depriving her of the opportunity to make a second bet. Not so. We’ll take a more “realistic” position, that she is going to bet $3.00 on the outcome. Let’s say the coin is unbiased. In the tails timelines an improbably generous bookmaker offers her the true odds, i.e. evens. Betting on tails, she would win $3.00, but betting on heads she would lose $3.00. You claim that in heads timelines, she would lose $6.00 betting on tails, but win $6.00 backing heads, therefore – across both timelines – her expectation from betting on heads is +$3.00.
But what you have totally failed to take into account is that SB’s induced confusion over the day – Monday or Tuesday – is entirely confined to SB’s mind. If you can find me a bookmaker so improbably generous as to take a bet on the winner after the stewards have ruled on the photofinish, I’ll get rich, too. In the real world, AND IN ANY BRANCH OF A CREDIBLE EVERETTIAN MULTIVERSE, SB breaks even with a fair coin, and loses when the true probability of tails is 1/2 < P(t) < 2/3 – i.e. all those other fairy tale scenarios where "thirder logic" suggests she should have "credence" that she would win.
The "credence" involved was defined as an assignment of probability out there, where the heads-tails uncertainty is resolved. That probability is known, and if you believe in it you give it credence.