Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
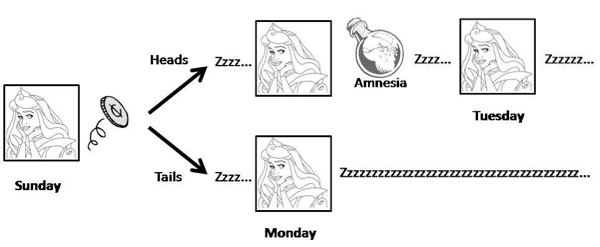
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
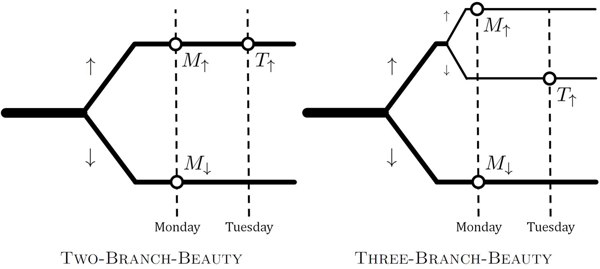
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
Another slightly tricky “did we obtain new info” example:
You know one ball out of 12 weighs less or more than the other 11 that are all identical.
You split them up 6 and 6 on a lever weight.
Will you learn something new?
(The challenge of the full puzzle is to not only identify the “fake” ball in only 3 weightings, but also to tell if it is lighter or heavier than the others.)
DN,
Well I would say that the induction steps occur in the modelling – the inference about the inference – which each blue eyed islander makes and so shouldn’t be considered the knowledge learned in the ‘real’ setting. So what the ‘real’ islanders learn from the guru is just that they actually are in the setting of the puzzle, and each blue eyed islander deduces that if the 99 others they can see are still there on the 100th day, their own eyes must be blue too.
Sean Carroll’s modified SB story where he inserts atomic spin for it’s quantum implications, but it is actually not a quantum problem as there is no imaginary dimensional quanity, so no need to square the wave function to get the probability. Could not follow his logic about the observers, where exactly are they and what they are observing? Not clearly defined and there is another problem of why he put an up arrow on the top lower Tuesday rung.
phayes,
thanks, that’s a great way to put it, I think. I usually have liked to point out that we somehow “need something to get the induction rolling”, but it might be better to paraphrase the situation after the Guru speaks as:
“Oooops, so now it certainly seems like I am in the blue-eyed puzzle scenario with all the well-known consequences. I damn better wait and see whether those 99 blue-eyed islanders around me are here on day 100”.
The concise proof given here:
http://terrytao.wordpress.com/2011/04/07/the-blue-eyed-islanders-puzzle-repost/
also doesn’t make any use of any higher order “common knowledge”.
I could have sworn I just submitted a comment. Does this blog have a glitch? What is the probability that a coin flip is tails?
Answer: 1/2
Phayes, Daniel Kerr,
Certainly the result of the trial is encoded in the number of times the wake-question routine is run; unfortunately that information is explicitly withheld from SB – else the puzzle evaporates. The thirders thinking is that since SB will be asked twice after a heads result, being asked on any one occasion is twice as likely to occur after a heads result as opposed to a tails result, which is true; but this is then bizarrely supposed to imply “possible universes” where the heads-result universes outnumber the tails-result universes 2:1. The experimenters have created a multiverse of sorts by a whimsical Groundhog-Day choice of protocol.
Meanwhile, in any one universe – and, to those of us who are multiverse-averse, there is only one universe – the trial was always a 50-50 proposition. There is no elimination of an outcome à la Monty Hall, no extra information.
Here is an easy non-Groundhog-Day parallel. The Unsleeping Beauty is told that a coin will be tossed. If the result is heads, the words “Trial Completed” will be written down twice, i.e. on two separate pieces of paper. If tails, only once. UB will subsequently be given a piece of paper on which the magic words appear, and asked to assign an a posteriori probability to a tails result. If the result was tails, the two pieces of paper for the heads result just don’t exist, they don’t get to vote if you like, except in the multiverse. In fact it is just such paradoxical results that cast doubt on the multiverse concept.
Logicophilosophicus,
Well I’m averse to multiverse mind-projections too and I’d be mortified if I thought the “thirder” position, if correct, somehow gave support to the ‘reality’ of some of the concepts used to arrive at it. But there is no need to worry about that, and resist accepting the “thirder” S.B. solution itself, because a single universe, ‘pure’ probability calculation (like the one I posted upthread) also arrives at the “thirder” position.
The SB “problem” is not really a problem. It’s a very interesting opinion poll.
The experimenter tells SB:
“Next week, I am going to wake you up once, and kill you 5 mins later, the day of the week determined by the roll of a dice.”
SB credence in being killed on any one of the 6 days: 1/6
SB is put to sleep, then woken up.
“SB already knew she was going to be woken up for sure, so she has no new information. Hence, SB credence in being killed on any one day of the week is still 1/6. Specifically, she has credence 1/6 that she is going to be killed today.”
Surely this is sound reasoning!?!? ^^
Logicophilosophicus,
In your example with the pieces of paper, there is a subtle change compared to the SB problem. Your problem is an analogy to a change in the SB problem such that the SB is awakened on either Monday or Tuesday, not both. In that case, the odds are 1/2 (trivially).
Phayes,
I think you are missing something: the three waking-askings, and the three slips of paper, and (in my earlier version) the three tokens simply do not coexist. There is therefore no meaning to the idea of drawing from that non-existent population.
Of course, in a multiverse they coexist; but then we are excluded from drawing from them. And, if we want to be really silly, we can imagine poor SB trying to factor in all the alternative realities where she misremembered the protocol, or the experimenters misexplained it, or the universe just popped into existence on Monday night. Everything happens in an infinite multiverse: here be dragons – don’t go there.
DN,
You’re right, of course, that there is a difference, but it is not useful to SB.
a) The proposition “The result was heads” is encoded as (or has the same “truth value” as) paired waking-asking episodes.
b) If it’s Tuesday, the evidence has been totally destroyed, of course. If SB knew it was Tuesday, she would reason: “There is a 50% chance I was woken yesterday, dependent on a 50-50 coin toss.”
c) If it’s Monday, the evidence will be destroyed before it becomes evidence, since there are not (yet) paired or unpaired waking-asking episodes. If she knew it was Monday, she would reason: “The evidence isn’t in yet – the coded message isn’t complete – so all I can say is that a coin toss is a priori 50-50.”
d) If she doesn’t know whether it’s Monday or Tuesday, she can reason: “I suppose I should take some kind of weighted average of the Monday and Tuesday situations – but whatever weighting I choose, it’s going to come out at 50%.” (Just to be clear: the weighted average the thirders want is that 2/3 of all possible waking-asking episodes are tied to heads; fine, 2/3 of 50% + 1/3 of 50% = 50%…)
Destroyed evidence is here entirely equivalent to withheld evidence i.e. no evidence.
The SB experiment is tweaked to consist of 1000 weeks, 1000 coin flips, etc. The SB is never told which weak it is when interviewed.
Everybody agrees that a random awakening is now 1/3 tails?
The SB now applies halfer logic, though.
1. “If this awakening is in week 1, then tails credence is 50%. If week 2, also 50%, and so on and so forth.”
2. “Since the credence is 50% in every week, and every week is equally likely, the credence of my current awakening is 50%.”
Of course, this reasoning is wrong. The credence is not 50% in week 1, or in any other week. Indeed, why should it matter if she is suddenly told “by the way, this is week 267”?
This example illustrates what can happen if you, for some reason, try to insist on other odds than the “long-term betting odds”. Like saying “this is only one week, where heads, or tails, but not both can happen, hence the odds are different than the long term odds.”
If you do that, it’s trivial to expand your “one time only” experiment to a “many times” experiment that has the same odds as your “one time only” experiment, leading to a contradiction with already established “long-term betting odds”.
Logicophilosophicus,
You write: “If SB knew it was Tuesday, she would reason: “There is a 50% chance I was woken yesterday, dependent on a 50-50 coin toss.””
Knowing it’s Tuesday, she surely gives a 100% chance to being woken yesterday?
DN,
Sorry, my last was misstated. I was conflating two versions of the puzzle – my (b) belongs in the interesting SB-not-woken-until-Tuesday-if-tails version: worth discussing, but we weren’t.
In the original version, b) should read “… So it was heads – probability therefore not at issue.” (Hence my “What is an a posteriori probability?” remark.) SB can lay odds against an undetermined result, but that does not apply here.
I don’t feel I’ve expressed that very well. The real issue (for thirders) is that the population of three waking-askings does not exist.
Logicophilosophicus, are you really surprised by the result that probabilities might vary depending on the observer? In this case we have an absolute universe where the probability is 1/2, but every “measurement” sleeping beauty takes, she’s biased simply by the methodology of that measurement. That’s all this puzzle is getting at. Sleeping Beauty’s universe is different than the experimenters, the good thing is that it’s strictly a subset of absolute universe here because her universe is constructed via biased sampling on the original.
Logicophilosophicus,
I agree with your revision:
If Tuesday, then it’s 100% heads.
If Monday, it’s 50% heads.
Now, as you suggest, we can do a weighted average. And without giving precise odds for the day, we can at least agree that the chance for Tuesday is more than 0%. And then the weighted average trivially sums to more than 50%.
So if one wants to save the 50% credence, one ends up having to claim another credence on Monday, before the coin is tossed.
Some people do this (and claim 2/3 Monday chance), but this can only work if you change the protocol of the experiment to be either Monday or Tuesday, but not both (in case of heads). And this would require a coin flip before the wakening up decision on Monday, unlike in the real SB experiment.
I don’t see this as a problem at all. Consider this provocative revision:
If heads, 1 awakening.
If tails, 1 awakening.
Here, as you say, the population of two waking-askings does not exist. Still, we have no problem giving 50/50 odds.
I agree that it’s a confusing issue that the SB is waked-asked more than one in case of heads. But once you do the math then, it’s going to be 1/3 for each waking-asking (but only because it is a fair coin etc.).
DN,
First, your “provocative revision” – there is “no problem” because we assign the 50-50 odds without any consideration of the awakenings. We assign it because the coin has two sides, and from that population of two we are going to select one at random.
Back to the awakenings, there is no population of three.
Even if there had been such a population, the two awakenings for heads are not even partially independent, so there is no reaching into the jar twice: two of the candies are stuck together. But there is no jar. The only choice was made by the toss of a coin.
I could have made this a lot easier by pointing out that this was (in a sense) resolved decades ago after heated correspondence relating to one of Martin Gardner’s “Mathematical Games” columns in Scientific American. The puzzle was (as near as I recall): “A woman has two children; one is a boy; what is the probability that the other is also a boy?” The end result of a discussion somewhat parallel to the above was that “the” answer depends on whether we select the women and look at their families, or select the boys and look at their families. It is assumed that both children are available for classification. In the SB problem the “children” are wake-ask and (tails + Tuesday) don’t-wake-ask. The amnesia requirement guarantees that the ambiguity is hidden and therefore unresolvable. We don’t get to pick on the basis of the kids, just the mothers – heads or tails.
Sure, the boys puzzle depends on whether you specify the boy:
1. “One of the children is John, a boy.” 1/2
2. “At least one of the two children are a boy.” 1/3
Anyway, the SB puzzle. The point of asking about the provocative
If heads, 1 awakening.
If tails, 1 awakening.
case is to make it obvious that we are talking about possible worlds, not realized worlds. I claim that the reasoning to reach 50% here is:
1. How many awakenings are produced by the protocol, on average? 0.5*1+0.5*1 = 1
2. How many tails awakening are produced, on average? 0.5*1 = 0.5
3. Ratio of tails awakenings is 0.5/1 = 1/2.
Consider instead a roll of a dice:
1: 1 awakening.
2: 1 awakening.
3: 0
4: 0
5: 0
6: 0
What are the odds for an awakening to be “even”? You can’t just say 1/6 now, of course, we HAVE to do something apart from just looking at the default 1/6 odds from the dice roll.
1. How many awakenings are produced by the protocol, on average?
—— 1/6*1 + 1/6*1 = 2/6
2. How many “even” awakenings are produced by the protocol, on average?
——- 1/6*1 = 1/6
3. What is the ratio?
——- (1/6)/(2/6) = 1/2
And the SB case:
If tails, 1 awakening.
If heads, 2 awakenings.
1. How many awakenings are produced by the protocol, on average?
——– 0.5*1 + 0.5*2 = 1.5
2. How many tails awakenings are produced by the protocol, on average?
——– 0.5*1 = 0.5
3. Ratio of tails awakenings to all awakenings:
——– 0.5 / 1.5 = 1/3
When SB is awoken, she can’t just ignore the protocol because “durdle, durdle, coins are 50/50”. She has to consider carefully what happens in the full experiment.
When you add prediction shares (betting) to the puzzle, the math becomes increasingly clear. Upon awakening, how much could she pay for the share “This share pays 100$ if the coin was tails”? If she pays more than 33$, she is going to lose money. Simply because only 1/3 of the awakenings are tails, and not 1/2.
I have given a concise proof why the odds could not be 1/2. (https://www.preposterousuniverse.com/blog/2014/07/28/quantum-sleeping-beauty-and-the-multiverse/#comment-7295910552604296032)
The “only” way to circumvent this proof is by changing the experimental protocol so that the SB was awoken either/or, not both. But the protocol is specifically designed so that she is awoken more often in case of heads than in case of tails – hence why there are more heads awakenings on average.
Consider a dice again:
1: 0.5 awakenings.
2: 0.8 awakenings.
3: 2.3 awakenings.
4: 0.2 awakenings.
5: 7.2 awakenings.
6: 1.7 awakenings.
Now halfer logic is tantamount to saying that we should “normalize” like this:
1: 0.5 awakenings.
2: 0.8 awakenings.
3: 1.0 awakenings.
4: 0.2 awakenings.
5: 1.0 awakenings.
6: 1.0 awakenings.
It’s just not warranted, and from a betting perspective it becomes completely absurd.
Final example. Compare
if tails, 0.5 awakenings
if heads, 5237 awakenings
to
if tails, 0.5 awakenings
if heads, 1 awakening
Do you really want to give equal tails credence in these two cases? Also when you consider betting? If yes, what is your tails credence?
Apologies if I’m being repetitious here, it’s a long thread. With issues of probability it is important to look carefully at the definition. To define P(X|Y) we repeat the experiment many times, count the number of occurrences of Y and of X AND Y, and P(X|Y) = N_(X AND Y) / N_Y. Here, by a reading of the problem, X = “Aurora is interviewed”, and Y = “the most recent flip was tails”. There seems to be general agreement that with this definition P(X|Y) = 1/3.
The halfer position seems to be that X = “the coin is flipped”, call this X’, that P(X’|Y) = 1/2 (true), and that P(X|Y) = P(X’|Y) because X and X’ are equivalent (no new information). But the halfer position is self-contradictory, since P(X|Y) is not = P(X’|Y). So X and X’ are not equivalent, “I will wake up” and “I have been waked” are not the same. The blue-eyed puzzle is indeed a nice illustration of new information that is not at all intuitive.
DN,
The boys thing actually goes like this:
a) We can assume that the family is selected from the population of all families; the one-is-a-boy statement is then generated.
b) We can assume that only those families with boys form the population from which we select – the one-is-a-boy statement is built into the protocol.
The assumption is that we can go on to see the other child while keeping track of the already identified child – no problem with identical twins, for example… But in the SB problem that assumption does not hold good, and the twins are always impossibly identical (SB can have no cue that she has, for example, been involved in the trial for three days rather than two, no sense that her perfume has worn off, her hair needs washing, her nails actually do just need cutting – so identical that, in the multiverse, being indistinguishable they are actually one and the same I suppose). The first phase, waking-1, is not only indistinguishable from waking-2, SB is not allowed to know whether it took place already.
Anyway, let’s not get bogged down. The thirder reasoning is that a waking chosen at random is more likely to be from a pair than a singleton. This statement could only be verified by looking at both: she can’t. The further inference to the likely result of the coin toss depends on that intermediate step. So, no, 1/3 does not work for me.
If the result is heads, we will tell you twice that the coin has been tossed, but you won’t know we’ve told you twice, you’ll only know we’ve told you. You will know the a priori 50-50 probabilities. Go figure.
Logicophilosophicus,
Let’s change the problem slightly. Let’s say if the result is heads, she wakes only on Monday and is asked what the result was. If the result is tails, she wakes every day for the rest of eternity and is asked the result. What belief should she assign to the result of the flip? Keep in mind, we’re not asking for the probability of the flip, we know she believes it’s 1/2, she’s not dumb. We’re asking for the result of that particular flip.
Daniel Kerr,
Memory-wiped then woken, we suppose. For the sake of avoiding a separate discussion about infinite-set paradoxes, let’s say she is woken every day for fifty years after a tails result. After even ten years she will be certain that it is not just next Monday, and that certainly highlights one of the sources of error in the puzzle – that the wakings cannot be identical.
Anyway, back to 2 indistinguishable wakings for, let’s say, heads, since that’s the version I’ve been assuming. We combine the SB puzzle instructively with its very different version, Bertrand’s Box. After the coin-toss trial, the experimenter picks up one of two boxes, looks in, and according to the protocol selects a gold coin, which he gives her. The protocol specifies that one box contains two gold coins, the other a gold and a silver. If the result was heads, the GG box must be picked; if tails, the GS box. Then the twist: if heads, SB is memory-wiped, the first coin is hidden, and she is given an apparently identical repeat performance, where the coin is of course the second G, though she cannot know this. Her rational thoughts at any particular waking are: “A 50-50 coin toss determined which box is picked; the experimenter’s selection of a gold coin was MANDATORY and therefore devoid of information; I have no reason to update the 50-50 expectation yet.” The difference with the original Bertrand’s Box was that there was a random pick of box and a random selection of coin, and therefore (and for no other reason) we could draw a statistical conclusion from the fact that a silver coin was not selected. In the SB version, a silver coin cannot be selected – the protocol bars that source of information.
Dr. Carroll
I was just reading a Salon article where Noam Chomsky claims that we had yet another near run in with worldwide nuclear annihilation with the Bin Laden raid. Add to that the India/Pakistan crisis of 2003, a misidentified Norwegian rocket in 1996, NATO’s able archer war games in the fall of 1983, and of course the Cuban missile crisis in 1962 and we have a lot of near misses with extinction. Is our string of luck just that or is the many worlds interpretation right and we have been conducting a worldwide quantum suicide experiment since at least 1945. What are your thoughts on our string of luck.