Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
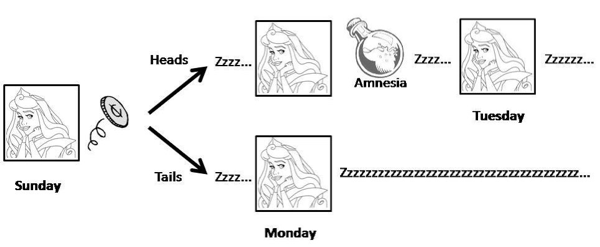
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
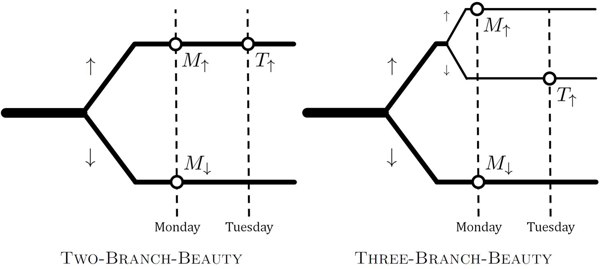
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
It’s nice to win the Dirac Medal, but what’s really cool is tricking people into upvoting your blog comment.
🙂 Well, anyone who dislikes the previous comment can downvote this one instead.
Now, given agreement on the mathematical fact of 1/3 for the previous question, a series of questions:
1. Suppose we tell SB that it’s the 97th interview. She then has all the information we have, so her probability is 1/3. Of course, this is a different situation, but…
2. Now suppose that we just tell her that it’s the 65th (or whatever) experiment. So she doesn’t know if it’s the 93rd, 94th, 95th, … interview. But it doesn’t matter: there was nothing special about 97, they are all the same. So her answer is again 1/3.
3. Now we don’t even tell her what experiment it is. The answer is the same, since the experiments are identical.
Joe why not make it even simpler and say that you only wake the sleeping beauty if it is heads and never if it is tails. According to the sleeping beauty the coin always comes heads so 100 % instead of 50 %. Your sampling is perfectly biased and the sleeping beauty thinks it is a coin with two heads.
The Monty Hall case has a similarly simple limit such that you choose 1 door out of a zillion doors + 1. The host opens a zillion doors – 1. Now you have two doors the one you chose at the outset and the only one the host left closed. The chances of guessing right if you switch is functionally 100 % for zillion sufficiently large.
The entire thing is an empty exercise that people get crossed in their heads.
Ignacio – The halfer logic is that SB learns nothing new upon waking: she knew that she was going to wake up, and she did. If on tails she never wakes then she does indeed learn something new and all would agree.* The halfer argument has an intuitive appeal, but with probabilities intuition often fails; one must do the math, which shows that this intuition is simply wrong.
*Well, I suppose there are some halfers who take an even less informed point of view: “The probability that a coin was tails is always 50-50.” Your example should show them that this can be influenced by new information.
Ok Joe I will leave you to it then but as Sean mentioned your Dirac medal will not help you here.
“Trial”: Flipping the coin and carrying out the waking procedure corresponding to the outcome of the coin toss.
There are 3 types of “events” to consider:
E1: waking SB on Monday after heads was thrown
E2: waking SB on Tuesday (after heads was thrown)
E3: waking SB on Monday after tails was thrown
In a large number N of trials, each type of event (E1, E2, or E3) will occur approximately N/2 times. Thus, the relative “trial-frequency “ for each type of event is 1/2.
In a large number N of trials, there will be a total number M of events that occur and M will be about 1.5 N. These M events make up a “pool” of events. Each type of event (E1, E2, or E3) will occur approximately M/3 times. Thus, the relative “pool-of-events-frequency” for each type of event is 1/3.
Based on the trial-frequency, the probability that event E3 occurs is 1/2.
Based on the pool-of-events-frequency, the probability that event E3 occurs is 1/3.
E3 is the only type of event for which a tails was thrown. When SB is awakened she can assign a probability of 1/2 for tails being thrown if she defines the probability based on relative trial-frequency.
Or, she can assign a probability of 1/3 for tails being thrown if she defines the probability based on a relative pool-of-events-frequency.
These are not contradictory assignments of probability. They just use different definitions of “probability that tails was thrown.”
Suppose we ask SB to say “heads” or “tails” when she is awakened and she knows we will pay her a dollar if what she says corresponds to what was actually thrown. She should say “heads” every time if she wants maximum payout after many trials. This is true even if she adopts the trial-frequency probability of 1/2 for heads or tails to occur. In this case she would state that the probability of tails is 1/2 and the probability of heads is 1/2. But, she knows that if heads was thrown then she will get paid twice in the same trial if she always says “heads”.
[Suppose you are asked to predict heads or tails for a fair coin toss. I tell you that I will give you 2 dollars if heads occurs and you predicted heads and I will give you 1 dollar if tails occurs and you predicted tails. Clearly, you should always predict heads even though you would assign equal probabilities of 1/2 for heads or tails to occur.]
Tom,
Yes, the coin-flip trial frequency is 1/2 for each outcome. But SB is asked for her credence in the outcome of the flip. That is, given everything she knows (the background information about the experimental procedure, and that she is awake during the experiment), what is her credence that the coin came up heads vs. tails? And that has to be different from the prior assessment of 1/2, because it is modified by the knowledge that she is in one of the three possible events described by “in between being awoken during the experiment and learning the outcome of the experiment”. In those moments (but only in those moments), she must assign probabilities of 2/3 and 1/3, respectively.
Modify the experiment as follows: At the start of the experiment, there are four boxes. Two boxes contain 5 pounds of iron. One box contains 5 pounds of gold. One box is empty.
SB will be awakened both days. Amnesia drug is still given when she goes back to sleep.
If heads was flipped, then on the first day she will be handed a box of iron, and on the second day she will be handed the other box of iron. If tails was flipped, then on the first day she will be handed the box of gold, and on the second day she will be handed the empty box. The empty box weighs less than a pound.
SB is awakened and given a box. She can tell that it weighs several pounds. What is the probability that the box contains the gold?
The answer is 1/3, I think its pretty obvious.
But this has absolutely nothing to do with Quantum Mechanics.
Instead of waking/asking, suppose we tell SB that we will put a token in a jar if the result is x; if it is y we will put a token in the jar, later taking it out but immediately putting it back again. Clearly examining the contents of the jar at any moment (ignoring the out-in singularity) tells her only that the trial has been completed, and gives no extra information about the result.
There are not three separate states offering evidence. I’m a halfer.
Richard,
I agree that the “thirder” specification of probabilities is valid. It’s just that I have some doubt whether it is the only valid way for SB to specify the probabilities.
SB knows that in a large series of repeated trials:
1/3 of all awakenings will be “tied” to tails and 2/3 of all awakenings will be tied to heads.
1/2 of all trials will be tied to tails and 1/2 of all trials will be tied to heads.
A “thirder” is drawn to the first statement and takes the “probability of tails” to be 1/3. As I see it, by this she means nothing more and nothing less than that 1/3 of all awakenings are tied to tails.
But why can’t SB be a halfer and take the “probability of tails” to be 1/2? By this, she means nothing more and nothing less than that half of all trials are tied to tails.
It seems to me that both assignments of probability are valid. They correspond to SB adopting different definitions of “the probability of a tails”. You can start with the thirder probability assignments and deduce the halfer probability assignments. And vice versa.
I believe both a thirder and a halfer would agree on the answer to any “objective” question that can be asked regarding the scenario. For example, take this question:
Every time SB is awakened we ask her to predict whether heads or tails was thrown. What should she say in order to maximize the number of correct predictions?
You can easily show that both the thirder and the halfer predict that, in a large number of trials, there will be twice as many awakenings tied to heads as awakenings tied to tails. So, they both agree she should always say “heads”.
I don’t see how one could prove that the thirder interpretation of “probability of tails” is the one and only “correct” interpretation. If it is, in fact, the only reasonable interpretation, then it would not change the content of the problem to explicitly spell out this interpretation in the statement of the problem. Then, I bet almost everyone would agree on what SB should give as an answer to the question.
Anyway, as I see it there is an ambiguity in the meaning of “probability of tails” in the original wording of the problem. And that allows one to be either a thirder or a halfer. But everyone should agree on the answer to any “objective” question!
Joint distribution (probabilities x,y,z are unknown at first and x+y+z=1):
P(wakeup, monday, heads) = x
P(wakeup, monday, tails) = y
P(wakeup, tuesday, heads) = z
P(wakeup, tuesday, tails) = 0
By the problem statement we know that:
P(heads)=1/2, P(tails)=1/2
which implies (by definition of marginal probability) :
x + z = 1/2 => x=z=1/4 and y=1/2
So we can simply calculate the required probability:
P(tails|wakeup) = P(tails, wakeup)/P(wakeup) = P(wakeup, monday, tails) = 1/2
Germo, be careful with your probability assignments, I would define P(day, flip) first then define wake conditioned on them. When skipping steps it’s easy to miss insight.
Tom,
Since the question to SB is what probability *she* would assign, then we can’t really count trials as counted by the experimenter. We have to count what SB is cognizant of. For her, in her quest to hypothesize what she can about the current state of affairs, she sees a “trial” as an instance of being awake. The semantics of the experimenter, who sees a trial as a coin toss followed by a protocol dictated by the toss’s outcome, does not apply.
Richard,
When you say “she sees a ‘trial’ as an instance of being awake”, then it looks to me that you are redefining the meaning of “trial” from how I was using the word so that it would correspond to what I was calling an “event”. This could get confusing. I believe SB would understand and be able to use the word “trial” as I was using it.
May I ask you to give your definition of the phrase “probability *she* would assign for a tails” so that there is little or no leeway for interpretation of the phrase? If the words used in the statement of the problem do not have the same meaning to everyone, then it is not surprising that there will be differences in opinion on the “correct” answer to the problem. I’m not trying to be difficult, I’m just struggling to get to the heart of the problem. At this point, I believe that much of the disagreement between the halfers and the thirders lies in an ambiguity of “probability” as used in the problem statement.
Tom Snyder et al,
You’re right that there is a minefield for misunderstanding probability. (What IS an a posteriori probability?) But that has nothing to do with this puzzle.
Before the experiment, SB is told the protocol. She knows at that moment that she will be woken and asked the question. She knows no more when she is actually woken. The thirders are therefore claiming that the protocol predetermines the best estimate of the probability of the toss. (Knowing the protocol, if SB accepts the thirder “logic” she can say: “Save yourself the trouble of doing the trial – I know ALREADY that the answer will be 1/3…”)
In “The Hunting of the Snark” the Bellman nonsensically states: “What I tell you three times is true.” Are the thirders claiming that “what I tell you twice is twice as likely to be true”?
“She knows no more when she is actually woken.”
Of course she does. She knows that now it’s either Monday or Tuesday.
Phayes,
She did know it was going to be “either Monday or Tuesday” – it was in the protocol. She has nothing new requiring or enabling her to update her information about the trial result.
Logicophilosophicus,
More precisely: she knew she was going to wake up knowing that it’s either Monday or Tuesday. Her being told the protocol beforehand gave her enough information to model the trial and deduce [what] her inference [should be] during it.
Richard,
I am a thirder and all, but I think that your example with the gold and iron boxes doesn’t quite capture the intricacies of the SB experiment. Something “weird” or deceptive is going on in the SB experiment due to the drugging + repeated interviews and due to the 100% chance of interview when tails as well as when heads.
Slight change of setup:
1)
If tails, we produce gold bags. (according to some protocol)
If heads, we produce stone bags. (according to some other protocol)
2)
After this, we reveal our production (the bags, not their contents) to you according to one of three protocols:
A) (“You asked for a bag.”) OK, here is one of the bags, in case we made any bags.
B) Here are ALL the bags we produced.
C) We show you ALL the bags we produced, but one by one by using the drugging procedure.
What gold odds do you give during the reveal?
Under a lot of different production protocols, the choice of revealing protocol would not matter and nobody would dispute the heads and tails odds for a revealed bag(s). But in the SB case, the revealing protocol matters a lot, and I think this is what is hard to get an intuitive grasp on (when you are more used to operating in your mind with certain revealing protocols).
EXAMPLE 1.
If tails, we produce one gold bag 10% of the time.
If heads, we produce one stone bag 20% of the time.
Here the revealing protocol doesn’t matter, and I think that nobody disputes that a reveal event (in case anything is revealed) is going to be one bag with 1/3 gold odds. But notice how protocol B and C was the same as A only due to the fact that no more than one bag would be produced.
EXAMPLE 2:
If tails, one gold bag 10% of the time.
If heads, 2 stone bags 10% of the time.
Here the reveal protocol matters.
A gives 50/50 odds, in case we are shown anything.
B reveals one bag or two bags, in case we are shown anything. Of course, the last reveal looks entirely different than the first.
C reveals one bag at a time (with the 10% proviso), 1 bag in case of tails, 2 bags in case of heads.
I think some halfers may intuitively agree here that each reveal under C is going to be 1/3 gold. The point is that (as in example 1) the mind is led to notice that we may not always see a reveal, so we begin to think in frequencies.
Example 3:
If tails, one gold bag 10% of the time.
If tails, one stone bag 10% of the time, 1 gazillion stone bags 10% of the time.
A: 1/3 gold, in case we are shown anything (this is like in example 1 since we only ask for one bag to be shown pr. experiment).
B: 1/3 of the time we are shown one gold bag, 1/3 of the time we are shown one stone bag, 1/3 of the time we are shown a gazillion stone bags.
C: Might a halfer agree that any one reveal under C is going to be ~0% gold?
Example 4:
If tails, 1 gold bag 100% of the time.
If heads, 2 stone bags 100% of the time.
This is the SB situation.
Here it is my contention that halfers are somehow seduced by reveal protocol A due to the fact that a bag is now going to be revealed. Protocol A is now similar to saying “show me a bag” (while in the other examples, this is meaningless to say without the “in case any was made” restriction which leads us to think in frequencies).
So when the SB problem talks about an unspecified interview (at least one of which we know is bound to happen), halfers feel justified to think in terms of A, since this (coincidentally) always produces one reveal. “Since isn’t this what the SB problem is all about, one reveal (at a time)?”
Only it is not ONLY one bag revealed as pr. experiment description. We are INDISPUTEDLY asked to use reveal protocol C, which is some kind of hybrid between B and A. First we can say we give a middleman all bags produced (as in B), and THEN he reveals all of those to you by the drugging procedure.
I don’t really know what else to add (but all the different ways to explain this are surely helpful). If you look in discussion threads about the SB problem, practically all the halfer math presented (rather than just the “no new info” argument”) is based on using reveal protocol A, only one reveal pr. experiment. They justify this sometimes by saying stuff like “we need to split the pie in case of heads” which is really a tacit admission that they are now using protocol A.
They also sometimes give the “repeated bet” argument, that we somehow have to adjust for the repeated reveal in case of heads, which is, again, just another way to say that we should convert to protocol A rather than stick with protocol C.
I suggest trying to consider EXAMPLE 2 above. Hopefully a lot of halfers would agree that reveals here are going to be 1/3 gold, since we “have” to think in frequencies. Then one may note that the SB experiment is more or less the same as example 2, except we now choose to produce bags more of the time (but still with the same ratio).
Logicophilosophicus, nobody’s arguing that the number of times the question is asked affects the probability of the flip. The thirder position is arguing that if the number of times you are asked is dependent on the outcome, then you’ve been given more information about the outcome. Half of the time it’s tails, they are not bothering to ask you while every time it’s heads, you are being asked.
The doctor has a patient. The patient is sick with 50% probability, well with 50% probability.
If sick, the patient will visit the doctor 99 times in a year.
If well, only one time.
The doctor tells his assistant all this by year end.
The doctor then says: “Here are the notes from one of the visits.”
What are the odds that the notes are from a visit where the patient was well rather than sick?
*ALERT* The assistant can’t tell yet, since he doesn’t know the condition for being shown the notes…
“Here are the notes from one of the visits, as you requested.”
Then it’s 50/50.
“Something peculiar happened at one of the visits. Here are the notes from that visit.”
Then it’s 1/100 (with obvious nitpicking provisos).
“My dear assistant, I will show you the notes from all the visits, using the infamous SB drugging procedure.”
Then it’s 1/100, but halfers will say 1/2 since they conflate this scenario with the “request” scenario.
Here’s another puzzle in which the distinction between an inference and an inference about an inference is important. Without it, it appears the islanders learn nothing they didn’t already know when the Guru speaks, and the puzzle can remain somewhat puzzling even when the solution is known.
Well if SB is rational she will realize that there was only one coin flip and the odds are the same for it being heads or tails, so a 50% of it being tails. What are the chances of SB being that rational and not buying into that screwy thirder logic? You start getting into nonlinear processes now.
A real life example of non-rational or nonlinear thinking is the whole dark energy question. That logic goes like this we do not understand the expansion of the universe from what we are seeing so let’s invent dark energy, which we really do not understand, to explain it, just to not be arguing from ignorance.
Now nonlinear solutions can be rational also and if there is more than one possible conclusion from a set of facts, the most you can say is about the probability of any given solution.
phayes,
yes, that blue eyes puzzle is worth keeping in mind to remind us how easily one can overlook that new information is available.
I find it particularly easy to see that new information is available when you consider the case with N=2 blue-eyed islanders. Then one of them now knows that the other one knows that there is at least one blue-eyed person. Which he (the first one) didn’t know before the Guru spoke.
You can then explain the step from 2 to 3 with some expectation of acceptance to get things rolling, and from 3 to 4.
What I still can’t quite figure out about this puzzle is whether it is enough to have the islanders think “I know that he knows that” and then the induction logic will be enough on its own for the islanders (and you), of if you actually need to deal with a cascade of “I know that he knows that he knows that…” unfolding for each day passing in order to solve the puzzle.
http://en.wikipedia.org/wiki/Common_knowledge_(logic)