Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
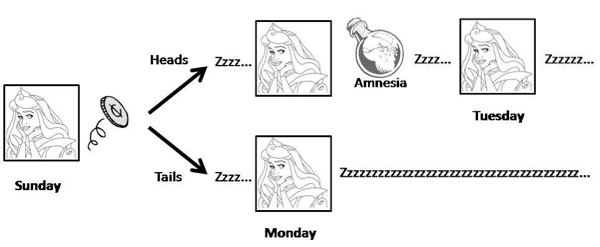
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
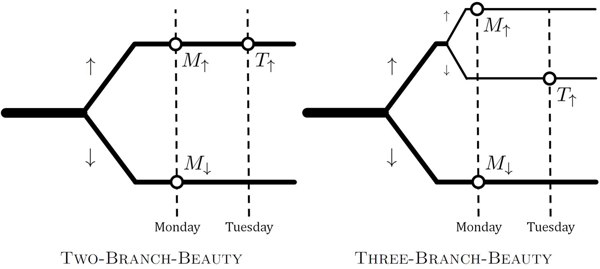
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
I think it’s useful to drop the assumption of a fair coin from the argument for the correct answer. Replacing that rather fragile-looking Elga/Wikipedia argument with a couple of expansions in conditionals yields P(Heads|.) = P(Heads|Monday, .)/(2 – P(Heads|Monday, .)) and the frequentist and non-frequentist arguments agree whatever the coin bias.
Any time you find yourself saying that the probability of each outcome is different from the the ratio of the occurances of each outcome after many repeated trials, you should realize that you’re doing something wrong.
Sorry Doc if I have commented here before, I have this short term memory problem . Were we talking about the paintings or that every time the stock market tosses a coin then I put a dollar into my no load index mutual fund? Did you know that the government (I forget which one) has a new deal and gives me another dollar in welfare/tax refund when the coin lands heads? So I get two dollars for every coin flip that lands on heads! My stock broker just called me and said the stock market flipped a coin what is the probability that it is heads or tails? If the stock market did 1000 coin flips today then what is the expected value of my portfolio?
@CB,
“I don’t think those two phrasing are actually different. “What is the most likely outcome of an event?” and “How would you bet on that event?””
I agree they are quite similar but neither one of them was the question asked SB.
The question to be asked beauty on each interview was: ‘What is the probability you would assign that the coin came up tails?”
There are no other qualifications to the question above in Sean’s scenario. In such a case I believe there could only by one right answer 50:50 since that is the exact indisputable probability of a coin flip.
However if instead she was told that her only objective was to make the most right guesses concerning the results of the coin flip, during the whole experiment, then was explained again how the experiment will go, she might then realize that if she guesses heads she can be right twice during the experiment if the coin flip is heads, but she could be right only once if she picks tales. In this case upon being explained this different objective, she might realize that her odds are 2 to 1 if she picks heads, and 1 to 2 if she picks tales for her guesses.
This is the “thirder” position. The key IMO is asking precisely the proper question for her to consider the 1/3 assessment. Although the odds for tales would be 1/3 based upon the guessing odds and the possibilities based upon both sides of the coin, there can only be two maximum interviews, and only one or two waking times in one coin toss and experiment.
Of course my argument is semantic, but the correct wording is important to come to the correct conclusion concerning the meaning of anything.
Daniel: Thanks, I understand your point better now. And I agree that I really mean ” wake on Monday”. Where I now disagree is your assignment of probability 1/3 to each day of the week. Days themselves do not occur randomly, and each day occurs exactly once following each independent random trial. So they all have probability 1, and are not mutually exclusive.
CB: Probability is what you get by applying the axioms of probability theory. It turns out that it may be calculated as long-run frequency over *independent* trials. My argument is that waking a on different days of the week in the SB problem are not independent.
JP, the days divide the probability space, from sleeping beauty’s point of view, it’s a random variable. It actually doesn’t matter though, as you could replace my whole analysis with wake|Mon or wake|Tue and you will get the same result.
Forrest noble, I disagree with the notion of probability you are arguing. You seem to be assuming there is an “absolute” probability at heart here, which in the example is the coin flip, but in practicality is not what we mean when we ask for a probability. A conditional probability is still a probability, and in full Bayesian formalism, every probability is a conditional probability. The problem is asking for the probability from the point of view of Sleeping Beauty. A lot of the times the question is asked, they don’t say “probability,” they ask what belief she should assign to the outcome of the flip.
Daniel: OK, I guess by “Monday” you mean the event “A particular day that SB was awoken is a Monday.” Fine, then we can create a sample space with the four exclusive elements “Monday, H”, “Tuesday, H”, “Monday, T”, “Tuesday, T,” as per your earlier comment.
Now the question is how to assign a prior probability to these four events. You have assumed a uniform prior. But SB knows all along that P(Tuesday, T) = 0 and P(Monday, T) = 1/2. The problem gives no principled basis for choosing P(Tuesday, H) and P(Monday, H), but we do know that P(Tuesday, H) + P(Monday, H) = P(H) = 1/2. We then introduce an event “woken” which is true for “Monday, T”, “Monday, H”, and “Tuesday, H.” So, finally, P(T | woken) = P(Monday, T) / (P(Monday, T) + P(Monday,H) + P(Tuesday, H)) = 1/2.
JP:
The probability of an event can be calculated by repeated trials of that event, full stop. The trials must only match the conditions of the probability you’re trying to calculate. If they don’t match, then they will differ, but that means either you’re doing the trials wrong, or calculating the probability wrong. In this case, the trials are correct by definition.
Events not being independent just changes how you have to calculate the probability. It doesn’t mean any event which was dependent on a previous one is ignored.
If a random number generator produces a 0 or a 1 with equal probability when it produces a number randomly, but every time it produces a 1 randomly it also deterministically produces a 1 the next time it is queried then reverts back to random behavior, you don’t say “well the second 1 is not independent so that doesn’t change the probability of getting a 1 away from 1/2 even though twice as many 1s are being produced as 0s”. Well, you do, but that’s incorrect — as demonstrated by you arriving at the conclusion that this RNG is fair when it clearly isn’t. Sorry.
CP: We both agree that events not being independent changes how you calculate the probability. In your RNG example, I certainly would not conclude that it’s a fair RNG, as it has serial correlations. In fact, in your example it’s basically meaningless to ask for P(1). You could ask for the probability of a 1 on trial t, P(1 | t), and then hope that it converges as t -> infinity. But this is provably not the case. You could also ask for the expected fraction of 1s, and this I agree is 2/3, but that’s not the same thing as a probability.
So your new answer to the SB problem is “undefined”? And yes, they’re the same. Every time you query the RNG, you’re asking it “At the time of being queried (awoken), what was the result of the last random selection (coin flip) — which could be either a fresh flip, or the same result as a previous flip as defined by the algorithm/experimental protocol.” And the question “What are the odds that the last coin flip prior to this query was heads?” is the same as the probability that the RNG answers 1.
The expected fraction of 1s is precisely the same as the probability of a 1. That’s what expectation means. That’s what probability means. There is debate over what probability means (if anything) with regards to a single trial — and I’m certainly in the camp that says that it is meaningful — but what *everyone* agrees is that probability is the same as what you would expect to see over repeated trials as t->infinity.
I guess except you, with your new “undefiner” stance?
The expected ratio of heads to tails is 2:1. If you don’t get 2/3rds for your probability, then you did the math wrong.
JP, your probability assignments are inconsistent. The arguments of your probability functions should follow propositional logic or set theory for the claims you are making. Your arguments clearly are not held to such a logical standard. P(Tuesday, T)=0 implies that given a sample space divided into partitions Heads, Tails, Monday, and Tuesday, the set of elements in Tuesday and Tails is empty.
Keep in mind you haven’t even defined the “woken” state yet on this probability space and you’ve already assumed that the Tails and Tuesday combination cannot happen. This is equivalent to stating that regardless of Sleeping Beauty’s experience/observations, Tuesday and Tails is not a possible event. P(Tuesday, T) is not conditioned on Sleeping Beauty’s observations, it’s an absolute claim for Tuesday and tails for all possible observers. According to you, not even the experimenters can observe this combination. You’re assuming the conclusion from the very beginning.
The fact is that all four of those cases each have a probability of 1/4. 1/2 of all events lie in Monday, the other half lie in Tuesday. Likewise for the coin flip. Because these two set of partitions are mutually independent, Heads and Tails splits each of those partitions by 1/2 too. So now when you substitute the correct probability assignments into your equation, you get 1/3.
CB: You’re right, my comment that P(1) in your RNG example is undefined was hasty. But I certainly have not changed my mind that the answer to the SB problem is 1/2, I just don’t think your P(1) is analogous to the quantity we wish to calculate in the SB problem.
Daniel: This comes back to semantics, and what exactly you mean by the events “Monday” and “Tuesday.” In the comment you’re replying to I am working under the assumption that “Tuesday” is shorthand for “A specific day on which SB woke up is a Tuesday.” This is how I understand your notation. With this definition it is certainly the case that the intersection of “Tuesday” and “Tails” is empty for all observers, including the experimenter.
You could instead define “Tuesday” as the event that “A Tuesday occurred during the week following the coin flip.” Then of course the experimenter may see a world containing both “Tuesday” and “Tails.” But then you have to give up mutual exclusion: P(Monday) = P(Tuesday) = P(Monday & Tuesday) = 1 and I’ve already addressed this case in an earlier comment. But if you want to hold that P(Tuesday & T) > 0 *and* P(Monday & Tuesday) = 0 then I fear you’re being inconsistent.
Or you can simplify the whole calculation, and not try to break the event “SB woke up on a Monday” into “SB woke up” and “Monday.” This straightforwardly gives the answer 1/2, assuming you agree that we’re calculating P(T | SB woke up on at least one day).
JP: If I were SB I’d define the events “Monday” and “Tuesday” as “Today is Monday” and “Today is Tuesday”: https://www.writelatex.com/1311844gmhppg#/3221529/
phayes: OK, but SB’s “Today” = “A day that SB woke up,” so this is the same as my phrasing “A specific day that SB woke up is a Tuesday.”
JP: Great, progress! Well, they’re exactly the same. Not analogous, identical.
The odds that the RNG returns 1 on a query is the same as the odds that the most recent bit flip it performed was a 1. It performs a bit flip prior to this determination if 1) the last coin bit was 0 or 2) the last bit flip was a 1, and the RNG has since been queried a second time. Otherwise (on that second query in the case of a bit flip 1), the bit is not flipped again and so the RNG returns the same value as before, which is 1.
This is exactly what is going on with SB. She is being asked what are the odds that the last coin flip was heads. Not *a coin flipped in isolation*, but the last coin flip prior to her being woken up and queried. A coin flip was performed prior to this question if 1) the last coin flip was tails or 2) the last coin flip was heads, and she has since been queried a second time. Otherwise (on the Tuesday when the Monday flip was heads), the coin is not flipped again, so the value of the coin flip is the same.
Literally the same except for the words used.
Remember, the question is not “considered in isolation, what would the odds of a fair coin flip be?”
The question is “Given these rules, what are the odds that the last coin that was flipped was heads?”
These are not the same. Since the rules state that the queries are not evenly distributed among coin flip outcomes, the odds are not the same as the coin flip considered in isolation.
Remember, it’s perfectly clear that the outcome of repeated trials will be heads 2/3rd, tails 1/3rd. Which means that’s the probability.
It’s just an issue of overcoming what you think the answer “should” be, and realizing that the answer depends on the rules, and the rules change the probability from the “simple” case.
No, JP, it’s P(T | She woke up). She wakes up twice for heads, once for tails, therefore P(T | she woke up) = 1/3rd.
Daniel Kerr- I should have mentioned you along with Ignacio as making convincing responses to the post.
I expect Sean will engage with these arguments at some point.
forrest_noble:
So, you feel that the question “What is the most likely outcome of the event?”, which we agree is “Heads, with probability 2/3rd” is different than “What is the probability the event came out heads?”, and that this answer is 1/2 (you specifically said tails but that’s 1-Heads in any case)? You realize that’s self-contradictory, right?
The halfers and the thirders differ in how they want to assign interview state probabilities (by state I mean, say, Tails and Monday, TM):
halfers: 1/2, 1/4, 1/4
thirders: 1/3, 1/3, 1/3
I suggest the halfers are essentially answering this question:
“Here’s an experiment. Now pick one interview from the experiment. Which state is it?
Since, in case of heads, we end up picking one interview and disregarding the other, we get a 1/2, 1/4, 1/4 distribution (and this, trivially, leads to a tails state 50% of the time).
While the thirders are essentially answering this question:
“Here’s an experiment. Pick all interviews from the experiment. Which states are they?”
The experiment produces 0.5 of each interview state, so this gives a 1/3, 1/3, 1/3 distribution (and leads to a tails state 33% of the time). Note that this equality with all being 1/3 is NOT due to them being “indistinguishable, thus equally likely”. It is just a coincidental consequence of the concrete values in the game (fair coin etc.). If the coin was, say, 70% tails/30% heads, then the distribution would be 7/13, 3/13, 3/13 (but the halfers would say 7/10, 1.5/10, 1.5/10).
To figure out why the halfers are wrong, let’s say we record all the interviews on video. Now the halfers will pick (“buy”) one and only one video from an experiment and then regard this as representing the SB situation.
But the SB doesn’t “shop” videos (or interviews) in this way. In case of heads, she also stars in the video NOT picked by the halfer, and when woken up, she can’t disregard that video from the set of possible states.
Let’s consider 4 weeks as illustration:
Week 1: Tails, halfer buys TM video.
Week 2: Tails, halfer buys TM video.
Week 3: Heads, halfer buys HM video. (And disregards the HT video.)
Week 4: Heads, halfer buys HT video. (And disregards the HM video.)
Now the halfer says that, see, 2 out of 4 videos are tail videos, so the correct answer is 50% tails. (And he will point out that 2/3 of the Monday videos are tails videos.)
But the SB, when woken up, will know she actually “was” (or will eventually be) recorded 6 times, even though the halfer only wanted to buy 4 videos (one video pr. experiment). Of those 6 videos, 2 are tails videos, while the other 4 are heads videos. (And half of the Monday videos are tail videos.)
Another way to put this is that the halfer desire to pick only one video pr. experiment and then wonder about its state is more or less arbitrary and only superficially similar to the actual SB situation (in that, of course, the SB can only star in one video/interview at a time). But the SB actually participates in 1.5 interviews pr. experiment, not just one. And of those interviews, 0.5 are tails, and 0.5 + 0.5 = 1 are heads (and this is what she is effectively being asked about).
You could say that the halfers are making a sampling mistake in that they calculate as if the SB is only interviewed once, no matter whether the coin lands heads or tails. (This is a little ironic of course, since usually it is the thirders that are accused of sampling bias by the halfers.)
An explanation somewhat similar to the above was given by Berry Groisman.
http://arxiv.org/ftp/arxiv/papers/0806/0806.1316.pdf
Liberally paraphrasing, he distinguishes between two different experimental setups:
1) Flip a coin, pick one video from the experiment, and show it to your wife. Which state is it?
2) Flip a coin, pick all videos produced and put them in a box. Keep doing this, and eventually have your wife pick a video from the box. Which state is it?
Now, the SB situation is not quite identical to either of these setups, but it is pretty much equivalent to 2), since the number of times the SB is interviewed depends on the coin clip. That is, to the SB, in each and every interview situation she is effectively picking from a box of 1.5 interviews, with only 0.5 being a tails interview.
CB: “No, JP, it’s P(T | She woke up).”
You’re not giving poor SB enough credit. She has two pieces of information: 1) She woke up today. 2) She may have woken up yesterday. She has to account for (2) in order to arrive at a rational answer.
JP, All I’m going to say is to be careful with your semantics. My calculation started with the most general use of days of the week and assumed no other structure. I absorbed this in my definition of “wake” and qualified it’s relationship to Monday and Tuesday via conditional probabilities. When I started the calculation, I was neither a halfer or a thirder, this was my first time seeing the paradox. Assuming the most basic probability assignments and nothing extra, I got 1/3. You’re playing a risky game with how you define terms in this problem, short-handing a lot of structure and conditional statements within single words. I was honestly surprised by the 1/3 answer until I analyzed what my calculation implied.
Let’s say you want to test the problem experimentally. Let’s assume that after running the experiment for 1000 weeks, you have 1000 coin flips – 500 heads, 500 tails – and 1500 interviews, 1000 of them after a heads coin flip, and 500 after tails. Every interview has the same answer, 1/3. What do you do with these numbers?
The flip-weighted probability is 1/2. The interview-weighted probability is 1/3. The question is asking for the interview-weighted probability; “Each time [that she is awakened] she is asked a question: …”
@CB,
You keep writing the question down wrong. You can understand the question best by quoting it verbatim. Semantics can change the opinion of the listener greatly if just one word is changed. Arguments based upon semantics can be a total waste of time. The wording of Sean’s scenario can by seen below again. You must write it down correctly word for word and then consider it from SB’s perspective.
“What is the probability you would assign that the coin came up tails.” This is the question that will be asked SB in her interview(s). This is the only question she will be asked. There is no other information given her excepting for how the experiment will be conducted. Remember the coin will only be tossed once for the entire experiment. She does not know that she will be graded based upon her answers. As far as she is concerned one guess is as good as another based upon a “fair” coin flip.
But if she were asked instead what do you think is the best strategy for you to come up with two correct guesses instead of just one for the experiment, she might realize that heads is the best answer by 2:1 odds, with 1/3 odds for tails being a correct guess in each interview, and 2/3 odds for heads being a correct guess in each interview, considering the possibilities (probabilities) of both sides of the coin.
Here is perhaps another way to look at this, which may make it clearer [to those to whom it is not already clear]. Suppose we repeat the experiment 100 times, so that there will approximately 100 wakings following a heads and 50 wakings following a tails. Suppose that we ask the question, “What is the probability that the 97th waking followed a tails?” This should be a routine exercise in probability, without any philosophical subtlety. I propose that you give this comment an up vote if you think the answer is [very close to] 1/3, and a down vote if you think it is [very close to] 1/2.