Hidden in my papers with Chip Sebens on Everettian quantum mechanics is a simple solution to a fun philosophical problem with potential implications for cosmology: the quantum version of the Sleeping Beauty Problem. It’s a classic example of self-locating uncertainty: knowing everything there is to know about the universe except where you are in it. (Skeptic’s Play beat me to the punch here, but here’s my own take.)
The setup for the traditional (non-quantum) problem is the following. Some experimental philosophers enlist the help of a subject, Sleeping Beauty. She will be put to sleep, and a coin is flipped. If it comes up heads, Beauty will be awoken on Monday and interviewed; then she will (voluntarily) have all her memories of being awakened wiped out, and be put to sleep again. Then she will be awakened again on Tuesday, and interviewed once again. If the coin came up tails, on the other hand, Beauty will only be awakened on Monday. Beauty herself is fully aware ahead of time of what the experimental protocol will be.
So in one possible world (heads) Beauty is awakened twice, in identical circumstances; in the other possible world (tails) she is only awakened once. Each time she is asked a question: “What is the probability you would assign that the coin came up tails?”
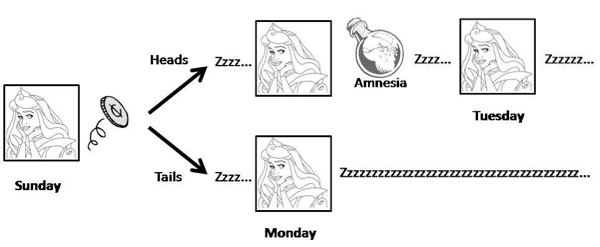
(Some other discussions switch the roles of heads and tails from my example.)
The Sleeping Beauty puzzle is still quite controversial. There are two answers one could imagine reasonably defending.
- “Halfer” — Before going to sleep, Beauty would have said that the probability of the coin coming up heads or tails would be one-half each. Beauty learns nothing upon waking up. She should assign a probability one-half to it having been tails.
- “Thirder” — If Beauty were told upon waking that the coin had come up heads, she would assign equal credence to it being Monday or Tuesday. But if she were told it was Monday, she would assign equal credence to the coin being heads or tails. The only consistent apportionment of credences is to assign 1/3 to each possibility, treating each possible waking-up event on an equal footing.
The Sleeping Beauty puzzle has generated considerable interest. It’s exactly the kind of wacky thought experiment that philosophers just eat up. But it has also attracted attention from cosmologists of late, because of the measure problem in cosmology. In a multiverse, there are many classical spacetimes (analogous to the coin toss) and many observers in each spacetime (analogous to being awakened on multiple occasions). Really the SB puzzle is a test-bed for cases of “mixed” uncertainties from different sources.
Chip and I argue that if we adopt Everettian quantum mechanics (EQM) and our Epistemic Separability Principle (ESP), everything becomes crystal clear. A rare case where the quantum-mechanical version of a problem is actually easier than the classical version.
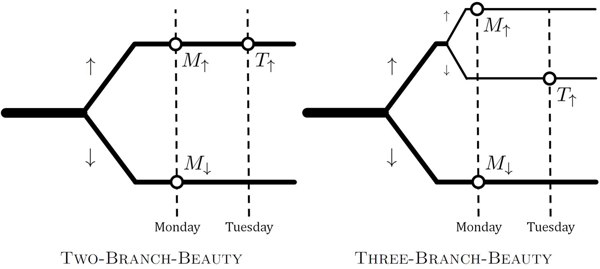
In the quantum version, we naturally replace the coin toss by the observation of a spin. If the spin is initially oriented along the x-axis, we have a 50/50 chance of observing it to be up or down along the z-axis. In EQM that’s because we split into two different branches of the wave function, with equal amplitudes.
Our derivation of the Born Rule is actually based on the idea of self-locating uncertainty, so adding a bit more to it is no problem at all. We show that, if you accept the ESP, you are immediately led to the “thirder” position, as originally advocated by Elga. Roughly speaking, in the quantum wave function Beauty is awakened three times, and all of them are on a completely equal footing, and should be assigned equal credences. The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder.
But! We can put a minor twist on the experiment. What if, instead of waking up Beauty twice when the spin is up, we instead observe another spin. If that second spin is also up, she is awakened on Monday, while if it is down, she is awakened on Tuesday. Again we ask what probability she would assign that the first spin was down.
This new version has three branches of the wave function instead of two, as illustrated in the figure. And now the three branches don’t have equal amplitudes; the bottom one is (1/√2), while the top two are each (1/√2)2 = 1/2. In this case the ESP simply recovers the Born Rule: the bottom branch has probability 1/2, while each of the top two have probability 1/4. And Beauty wakes up precisely once on each branch, so she should assign probability 1/2 to the initial spin being down. This gives some justification for the “halfer” position, at least in this slightly modified setup.
All very cute, but it does have direct implications for the measure problem in cosmology. Consider a multiverse with many branches of the cosmological wave function, and potentially many identical observers on each branch. Given that you are one of those observers, how do you assign probabilities to the different alternatives?
Simple. Each observer Oi appears on a branch with amplitude ψi, and every appearance gets assigned a Born-rule weight wi = |ψi|2. The ESP instructs us to assign a probability to each observer given by
![]()
It looks easy, but note that the formula is not trivial: the weights wi will not in general add up to one, since they might describe multiple observers on a single branch and perhaps even at different times. This analysis, we claim, defuses the “Born Rule crisis” pointed out by Don Page in the context of these cosmological spacetimes.
Sleeping Beauty, in other words, might turn out to be very useful in helping us understand the origin of the universe. Then again, plenty of people already think that the multiverse is just a fairy tale, so perhaps we shouldn’t be handing them ammunition.
I don’t get why there’s debate, this problem can be realized experimentally or in simulation, never mind simply calculating it in full probability theory formalism. I certainly don’t get the strong language being used on either side of the debate, there’s no reason to make this personal.
Daniel this has happened before as I mentioned concerning the Monty Hall. There should be no debate. You are quite right. These problems are not hypothetical. It is easy enough to program them.
But people get caught saying the wrong thing and then there is denial, anger, bargaining, disillusionment, and acceptance.
Now and again someone will get stuck at denial until he/she is forced to look at output from a code. It says a lot about humans, a little bit about probabilities and nothing about QM
I’m sympathetic to the claim that the problem is not that hard. Run the experiment many weeks in a row. One-third of the times that Beauty woke up the coin will have been tails, and two-thirds of the time it will have been heads. But it obviously is “hard” in the sense that many people disagree!
Also, the “quantum Sleeping Beauty” puzzle is not precisely the same as the classical one, at least in EQM where both branches actually exist. What Chip and I have argued is that there is a unique way of apportioning the credences that matches up with all the right expectations.
Any particularly convincing argument for the one-half position? the Bayesian sounding argument in the main post is incorrect I think: knowing the experimental protocol, SB certainly learns something from the fact that she is awaken, an event that is correlated with the outcome of the coin flip, and therefore should update her probability assignment accordingly.
Oh, sorry, Sean, missed that last comment. Still, since there is presumably a large body of work on this, some potentially confused but semi-convincing reasoning must exist…
Like the Monte Hall problem, I find the intuition significantly easier if instead of having only two days, to instead make the problem last say 100 days. (eg sb wakes up on monday and is put back to sleep, then wakes up on tuesday and is put back to sleep etc).
I do however agree that it depends a little on how you word the problem. I like the word ‘belief’ as opposed to probability here.
Suppose instead of “What is the probability you would assign that the coin came up tails?”, the question asked were “What are fair odds you would assign that the coin came up tails, such that you will have zero expectation value if you bet on these odds?”
Note that the problem stipulates that she will be interviewed on every waking. It is an unambiguous result in mathematics that the answer is 1/3, and even many halfwits see this. What is puzzling is that they interpret these two questions differently.
Maybe the issue is the distinction between probability and conditional probability. A clearer version can be that SB is woken only if the coin falls on heads (perhaps with a daily coin toss, for humanitarian reasons). When SB is then woken and is asked for her opinion of what transpired with that coin toss, a rational SB with any definition of probability should have no uncertainty about the matter, given that she is now awake. This does not contradict the fact that the probability for her to be woken up is only 50%.
@Joe Polchinski
You’re adding a random game on top of the original question and assuming SB’s answer to “What is the probability you would assign that the coin came up tails?” is the one that minimizes her own profit in this invented game. Any other answer would let her turn a profit by picking her guesses on whether it was heads or tails. You’re assuming the one who answers the question is playing _against_ SB when the problem statement clearly says _she_ is he one answering the question.
The key, of course, is the question “What is the probability you would assign that the coin came up tails?”. What is SB trying to achieve here? Any clear definition of that gives a clear answer, but my opinion is that any invention of games that doesn’t have SB answer honestly, as the problem states initially, that the probability is 50-50 _or_ that she can answer whatever she wants because nothing gives her an incentive to _lie_, is just plain stupid.
You can invent additional casinos or whatever that define what would optimize her expected value in iterated SB problems, but saying that 1/3 is the correct answer is just plain wrong unless you define a different game for which the answer is 1/3.
@Joe Polchinski
You can disprove my claims by specifying what SB is trying to achieve in a clear enough fashion and getting someone to bet against you despite this goal being clear to both parties.
SB’s goal is to assign probabilities to the possibilities that 1) she just woke up, and the coin flipped at the beginning of the trial was heads, and 2) she just woke up, and the coin flipped at the beginning of the trial was tails.
Since the experimental procedure clearly states that every time the coin comes up heads she will be woken up twice, and every time she comes up tails she will be woken up once, then it is obvious that over time the ratio of “woken and heads” to “woken and tails” will be 2:1. This is the same as saying the probabilities are 2/3 and 1/3. Literally the definition of probability.
So while she knows that the odds of a fair coin flip in complete isolation is 50:50, *that’s not the case here*, and the result of the flip has consequences, and those consequences mean that 2/3rds of the time she awakes in a universe where a fair coin landed heads. Therefore that is the correct probability to give. And repeated trials would bear it out.
Silly.
So an experiment with Sleeping Beauty is more important than an experiment by Alain Aspect?
I am assuming the coin flips are mutually exclusive and the semantics of the problem indicate that the event of “coin flip” and the event of “waking up” are independent events . Since sleeping beauty is guaranteed to wake up the probability of her waking up after a coin 50/50 coin flip is one.
P(Flip) = 1/2
P(Waking up) =1
If she has knowledge of what day it is that changes the semantics of the problem meaning that the mutually exclusive event of “coin flip” and the following event of “waking up” are conditionally dependent allowing her to assign different probability values (especially if it is a Tuesday). This appears to be a poorly worded problem. The problem most likely leaves sleeping beauty’s knowledge ambiguous to get people to ask the following question: What does sleeping beauty know and will she go out on a date with me (please check the box yes or no)? I could be wrong and what I love about probability theory is how it is deceptively awesome . Do I have any volunteers for this experiment?
P.S. Did you remove my earlier post? Because I could have sworn I posted here before.
It’s sleight of hand, no? The trickster gets us to focus on the odds of the flip rather than the number of interrogations that follow. Two-thirds of all interrogations follow heads and that is all we need to know
Ignacio’s comments here are convincing to me.
This post has solidified my impression that MWI is not an interpretation of quantum mechanics, but is rather a way of thinking about probability in the context of a single event. It doesn’t seem to say anything about where the probabilities come from.
The minimal interpretation seems to be the ensemble interpretation. Given that science is in the business of describing general rules, why would we ever care about the “probability” of a unique nonrepeated event? And for repeated events, all these puzzles go away, no?
Once you already have probabilities, what does it add to postulate an amplitude equal to their square roots? “The same logic that says that probabilities are proportional to the amplitudes squared also says you should be a thirder” seems trivially true, in the sense that if you have established probabilities by any means whatsoever, you should be a thirder.
I’m a layman whose opinion doesn’t matter. But Sean might want to know that, for one reader anyway, the effect these posts are producing is the opposite of their goal. (Though they are certainly serving their larger goal, of being interesting and informative!)
Below is the original question in Sean’s scenario.
“What is the probability you would assign that the coin came up tails?”
But for SB to come to the “thirders” conclusion something like this should have been the question IMO:
“What likelihood should SB assign to tails if she is told her sole objective is to guess correctly the most number of times?”
From this perspective SB might make a different choice than with the original question.
It also seems to me that the “thirders” position is not explained well above. In the SB scenario the coin is flipped only once. If she would guess heads for each interview and the coin flip came up heads, she would make two correct guesses, one on Monday and another correct guess on Tuesday. But if it comes up tails then she will be guessing wrong only once on Monday. So she is twice as likely to guess right if she guesses heads. This is the basis of the “thirder” position, but the wording of the question should have been different (similar to the “likelihood” question shown above IMO) for her to more likely come to this conclusion.
The answer is dependent upon the time frame. SB is being asked what the probability was for something that already happened based on what she knows. She has two clues to point to heads and one clue for tails. Therefore, she gives heads a 66% chance.
The 50% is what the coin flip could produce in the future. Now if I changed the story to say that when SB awoke she overhears the researcher say that the coin was tails then when asked what the chance was that it was heads she would reply zero. She was told what it was tails in this case.
In one problem we are trying to figure out the probability of a past event based on limited information. In the other it is what is the probability of it going to be. It’s a stupid little game and mind trick. I can’t believe all these PHD’s can’t see this.
JW Mason, I agree with you too. This treatment convinces me to view the set of universes as possible worlds in a modal logic framework, not in a “multiverse” view where each world is ontologically equal. I think the Ensemble Interpretation blends nicely with this approach since it would relax the assumption that the state is ontological. A key difference is that in MWI, upon making a measurement, the state branches into another quantum state. The Ensemble Interpretation argues that the universe itself never occupies a state, that a state gives you the distribution of possible outcomes and you are simply sampling values from that distribution. This avoids the preferred basis problem but still allows the same treatment of observers as Sean has carried out. I prefer to make less ontological assumptions with science, so even though I value Sean’s contributions to thinking of probability in a quantum context, I will just not be able to accept the universe is ever actually, physically in a wavefunction. I can accept it is the best possible description however.
forrest noble:
I don’t think those two phrasing are actually different. “What is the most likely outcome of an event?” and “How would you bet on that event?” must have the same answers if we’re talking about someone rationally trying to maximize their return, or number of correct guesses.
2/3rds of the time SB wakes up in a universe where the coin landed heads. That’s the probability, that’s how she should guess, and it’s the same either way.
The question that could have been asked that I think gets at your point is: “What probabilities would you assign to the chance *that the researchers, who are not subject to this sleeping/amnesia potion nonsense* observed tails?” In other words, breaking out of the experimental protocol into a different one where we’re just flipping fair coins over and over and that’s all that’s happening.
There’s nothing wrong with different observers observing different probabilities, that’s perfectly natural. And each of those observers can reason about what the other one’s subjective probability should be, given sufficient information about their situations. But I think it’s implicit in the problem that SB is being asked about her perspective.
But here’s a wrinkle: Imagine that SB *didn’t* know about the use of the amnesia potion in the protocol. She would say the odds were 50:50, and would have no choice but to guess at which came up. But let’s also say that she was allowed to record and reference previous results. It wouldn’t take too long for her to realize that the researchers must be up to some form of chicanery — a loaded coin? — because her rationalization of the probability is clearly wrong.
The answer is 1/2. It’s a straightforward application of Bayes’ rule once you accept that we aim to calculate P( T | interview ), and assume that P( interview | T ) = P( interview | H) = 1. Thirders should address which of these assumptions they disagree with.
Those of you applying a long-run frequency calculation to get the result 1/3 are neglecting the fact that “Monday & H” and “Tuesday & H” are not independent events. Indeed, they are completely determined by each other. So you can’t just aggregate them to estimate a probability. Incidentally, this is the error in Adam Elga’s paper linked to by the Wikipedia article.
The betting odds arguments are fine, but they calculate the value of a bet, not a probability. The problem asked for a probability. Given certain fixed conventions about the structure of the bet these two things are equivalent – as in, e.g. The Dutch book argument – but those conventions do not apply here (since the number of bets depends on the bet’s outcome).
JP, I calculated exactly what you claim to calculate in my first comment, except I added an extra interview on Wednesday. You can eliminate Wednesday from the calculation and you will get 2/3, all of my assumptions are clearly laid out, feel free to let me know what is incorrect. And I disagree, the problem is asking for P(T|Interview), which is not in general equal to P(Interview|T).
Daniel Kerr,
I believe the issue with your calculation is where you write P(wake and Monday OR wake and Tuesday) = P(wake and Monday) + P(wake and Tuesday). There’s another similar line in which the probabilities are conditioned on H. Since “wake and Monday” and “wake and Tuesday” are not mutually exclusive events you need to subtract P(wake and Monday AND wake and Tuesday). This is the same issue that I alluded to in my second paragraph.
JP, “wake and Monday” and “wake and Tuesday” are mutually exclusive events because Monday and Tuesday are mutually exclusive events. Simply conjugating Monday and Tuesday each with “wake” does not change this. Technically it should read “‘Monday or Tuesday’ and wake” as there’s no logical distinction between that and “‘Monday and wake’ or ‘Tuesday and wake.'” The latter is simply a more intuitive expression.
Daniel,
You’re effectively saying that P(wake and Monday AND wake and Tuesday) = 0. But this is clearly wrong, since when the coin comes up heads both events occur.
JP, no, that’s clearly right you have to concatenate it to see. “Wake and Monday AND wake and Tuesday” = “wake and ‘Monday and Tuesday.'” Monday and Tuesday are mutually exclusive, it can’t be both days at once. You’re confusing waking on Monday and waking on Tuesday with these notions. What you want is “Monday -> wake” and “Tuesday-> wake.” In probability we’d represent these as P(wake|Monday) and P(wake|Tuesday) respectively. These conditional probabilities are independent and equal 1 and 1/2. However, P(wake|Monday and Tuesday) has no evaluation as “Monday and Tuesday” has a 0 probability of occurring.