I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
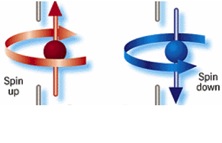The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
Neil, ah, I see, you’re tackling how MWI would handle constructing the initial universal wavefunction, which must exist whether measurable by inference or not.
In terms of the structure implied by such an analysis: Since any future state would have to be a time evolution of some initial state accounted for in the initial state representation, then you would represent this future state as an infinite product of projection operators. The problem is picking the basis of the projection operators so I think this is the preferred basis problem manifesting in yet another way. The infinity of the nesting is not the problem, a convergent product of mappings can be defined for a set of projection operators, but the convergence depends on this basis. One could backwards solve which kind of bases would be acceptable, I wonder if such a study has been carried out in the context of the preferred basis problem. My intuition says that the only acceptable basis for such operators should belong to the subset of the Hilbert Space that is Lp integrable.
We will start with the Schrodinger equation:
$latex i \hbar \frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\bigtriangledown^2\Psi $
The wavefunction that satisfies the above equation is:
$latex \Psi = \Phi(x)e^{-i \hbar E/t} $
Analyze the LHS of the equation which is a first derivative with respect to time:
$latex i\hbar\frac{\partial\Psi}{\partial t} = (-i\hbar E)(i\hbar) \Phi(x) e^{-i \hbar E/t}\newline
i\hbar\frac{\partial\Psi}{\partial t} = -\hbar^2 E \Psi $
Now remove the imaginary number from the Schrodinger equation and the wavefunction to provide a real diffusion equation:
$latex
\hbar \frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\bigtriangledown^2\Psi \newline
\Psi = \Phi(x)e^{\hbar E/t}
$
Again take the derivative on the LHS of the diffusion equation:
$latex
\hbar\frac{\partial\Psi}{\partial t} = (\hbar E)(\hbar) \Phi(x) e^{\hbar E/t} \newline
\hbar\frac{\partial\Psi}{\partial t} = -\hbar^2 E \Psi
$
There would be no debate about the interpretation if the Schrodinger equation and the wavefunction did not have imaginary numbers. We would also not be able to deny that time is real and an observable just like energy, momentum and spin. The core nature of the universe is random. When we measure an observable the equation must give us a real number and those numbers are described by probability theory. The results of the equation are identical with or without the imaginary number. Those who favor the Copenhagen interpretation cannot argue that it becomes real only when measured and when the imaginary numbers vanish by the born rule. It is sad that everyone accepts statistical mechanics but no one will accept calling quantum mechanics a diffusion equation with an associated diffusion function .
@Boltzmann: What you are suggesting, Schrodinger eq. with real functions (without i) has been tried numerous times in the last 100 years or so. It does not work! Quantum mechanics is a subtle inter play of complex functions to explain wave particle duality. Phases in the complex functions play very crucial role in the interference phenomenon which is the central issue in quantum mechanics. It is difficult to explain all this in a comment. But you may want to go through a book on quantum mechanics and try if it works with real functions. I can assure you it will not.
Physical theories should not have an assumption as their base foundation.
In MWI it is assumed the particle does not travel through a single slit when it is not detected.
There is physical evidence the particle always travels through a single slit, and that evidence is it is always detected traveling through a single slit.
There is physical evidence dark matter waves. It ripples when galaxy clusters collide.
de Broglie wave mechanics and double solution theory is supported by the physical evidence the particle always travels through a single slit and the physical evidence the dark matter waves.
In de Broglie wave mechanics and double solution theory the particle travels a well defined path through a single slit and the associated wave in the dark matter passes through both.
@kashyap vasavada: Is that worth a Nobel prize too? If only there were some way to do interference with the real numbers. Oh well maybe we will figure it out after an additional six years. I shouldn’t have called myself Boltzmann either because appealing to authority is a fallacious trick in an argument, my apologies. Thank you for reminding me to read books. I like books and I will keep my opinions and derivations to myself.
@Bored: Sorry. I did not mean to belittle your effort in any sense. In science, every one should have a right to put forward his/her ideas. Only requirement is that one should be aware of what has been tried before. All I wanted to point out was that such things have been tried before and have not worked and complex algebra plays an important role in quantum mechanics. As a matter of fact some very prominent physicists such as Weinberg and ‘t Hooft may be looking for alternatives to quantum mechanics.
@kashyap vasavanda: What a bummer that it has been tried before. In your opinion how do we order the complex numbers to provide us with the real numbers needed to make sense of observables? Do we take the inner product of two orthogonal wavefunctions and then take the square root? Isn’t that just squaring and then taking the square root of imaginary numbers? I can write it out in LaTeX if you would like. I deserve being belittled because I am trying to pick a fight. I respect Weinberg and t’Hooft but they shouldn’t be the only ones who get to have all the fun. What is your approach to doing quantum mechanics with real numbers?
@kashyap vasavanda: I was hoping that you would notice that a true wave equation is a second order derivative with respect to time. This allows us to take the derivative of an exponential complex wavefunction twice to cancel out the i’s and in this case we do not have to consider the ontological nature of imaginary numbers. Combinatorics and probability theory are also able to create functions which make valid predictions with real observables by using real numbers. Combinatorics and probability theory also tells us why the observables have the probability values/expectation values that they do. When we use a diffusion equation which is first order with respect to time then the probability amplitudes may be complex because we insist on using a complex exponential diffusion function. However, we do a lot of unnecessary work to map the observables and their probability amplitudes to the real numbers. We also do not need the imaginary numbers to explain wave particle dualitybecause that is not the fundamental problem. The measurement problem is why do we measure a particle once and find it in a particular state and then if a second measurement is performed it is either in the same state or it has the possibility to evolve into a different state. A solution to the measurement problem is an entropy argument which we are able to derive once we accept the postulates of the ensemble interpretation and that time is a real observable.
I have read about a science respectability checklist. However, my philosophical crisis is that publishing appears to be a sadomasochist initiation ritual more than a valid way of doing science. Yet to get paid to do science, mathematics and philosophy then I must publish. My salary or status within the community will then be correlated with the number of references my publications receive. If this post has at least 3 likes and or 3 dislikes then that should not change your analysis of my arguments. I ask annoying questions, the Socratic method, to determine what people in a forum understand and what they don’t understand. I troll because once people think I am a boorish rube then they are more likely to expose their own logical fallacies. Thank you for engaging in a dialogue.
I thought there are many labs now researching dynamical collapse, and that they can slow it down and even reverse it a little. What do you mean it hasn’t been witnessed?
Anyway, MWI does not follow trivially from basic quantum mechanics. It includes the extra assumption that the state consists entirely of a tree structure of paths through state space, which evolve indefinitely with effectively classical behavior and negligible interference with the rest of the state — using only deterministic linear dynamics.
@Bored, Dat is Jammer and Geen Probleem:
I responded to the original question because I did find it interesting, although it has been agreed upon for several decades that complex algebra is the correct way to do quantum mechanics and its extension quantum field theory. Although wave equations are second order, one starts with Schrodinger eq, (first order in time) and Dirac eq. (1st order in both time and space). I accept this conclusion, but if you want to proceed with real functions , then surely it is your prerogative, As for me I am more interested in the debates about interpretations. Surely there are problems with quantum mechanics such as quantum gravity. But they have nothing to do with the fact that we are using complex numbers. If you are interested, importance of complex algebra is explained in a semi popular book by a famous mathematical physicist Penrose “Shadows of the mind (Ch. 5)”. According to my understanding, in optics and electricity magnetism (also electrical engineering) complex numbers are just nice tricks to make algebra easier. But in quantum mechanics they play essential role.
Geen Probleem, this harping on complex numbers is just silly. You could represent the whole algebra of unitary quantum mechanics in a real valued spinor representation which is isomorphic to the Hilbert space over the field of complex numbers. The complex numbers do not belong to the theory, they merely represent the operations in it. Observables are not related to them. It is most convenient to have a complex representation, but you don’t have to. Good luck talking to everybody else using a needlessly complicated representation just to avoid “i.”
When I try to conceptualize MWI, I find it easier to think of an infinity of superpositions rather than an infinity of universes. The “doubling event” portrayed in most cartoon representations of MWI seems to be a big hang up for a lot of folks, both expert and amateur (I’m definitely in the latter category). When does it happen exactly? Is energy/mass really doubling? Etc. Is there anything specifically wrong with thinking about this approach as many superpositions rather than many universes?
Of the “four versions of QM” represented in the earlier post, it seems to me that MWI and QBism have the most in common. The “collapse” and “pilot wave” models both predict something not already in the equation, which is testable at least in principle. Can the same be said for MWI versus QBism? They both purport to take QM at face value, so I guess the answer might be no. Funny that Sean appears to dislike QBism more than the other two – is that because it’s the best contender to MWI? If it’s just personal preference, it’s hard for me to say whether I prefer that “everything that can exist does exist” (MWI) or “everything is just relational” (QBism). But those two things seem like they might be the same thing. Infinity of universes versus infinity of relationships. What’s the difference?
@Collin237: Are you saying that if we can slow down a collapse and reverse it then we would be altering the evolution of wavefunctions in other universes? All joking aside many have brought up an energy argument against the universe diverging at each quantum event. Would creating a new universe require creating additional energy? I would think it would take a lot of energy to copy all the information inside of each universe. Would that mean rethinking the laws of thermodynamics if we accept the many worlds interpretation? I understand the appeal of the many worlds interpretation because it is a way to keep a the wavefunction continuously evolving without ever collapsing. However, are we be able to falsify this interpretation?
@kashyap vasavada: I know using complex algebra in quantum physics has been agreed upon by everyone except for a few holdouts. Is there more than one way to solve a physics problem or only one exact way? The wisdom of the crowd can be a great shortcut to quickly find an answer or an interesting physics forum. Determining if that answer is valid can be difficult. If you are able to do quantum mechanics with real numbers then does that change the way you think about nature? I know that my thought process changes when I solve a problem in a different way, but that is my anecdotal experience.
Is the essential role of complex numbers to provide the time evolution of the wavefunction between measurements and the interference of wavefunctions? Calling a diffusion equation a wave equation must be incredibly confusing for physics undergrads too. The Copenhagen interpretation tells us that the wavefunction is not real until it is measured. Does that mean the wavefunction is not real because it is just a statistical ensemble of possible states or that the wavefunction becomes real once the imaginary numbers are mapped to the real numbers? I know this is semantics but I would appreciate the clarification.
I assume the wavefunction describes the probability of an outcome and that between measurements a particle may be switching states randomly. I also assume that in the act of measuring the particle it may or may not diffuse into a different state afterwards. Is the purpose of a waveguide to ensure that the energy/power of a wave does not diffuse into the environment?
Let’s assume you are unfortunate enough to have me as physics student. You assign your quantum physics class a weekly homework problem set. However, you are too busy writing grant proposals to grade the homeworks. You decide to distribute the quantum homeworks back to the class to be graded. You know that I am a crafty physics cheater and you also want to make sure that no one in the class receives their own homework to grade. What is the probability that no student grades their own homework?
Quantum gravity is a tough problem. Knowing the temperature or change in velocity of a single particle must be difficult to do experimentally especially with an uncertain velocity observable. The acceleration vectors of identical particles may interfere in weird ways or produce a unique acceleration vector field . What was the difference between special and general relativity?
@Daniel Kerr: I agree that the complex numbers do not belong to the theory, however, they can be useful. I believe I saw a post earlier from you on lie algebra and “real valued spinor representation which is isomorphic to the Hilbert space over the field of complex numbers” would make a great band name. The concept of an infinite dimensional Hilbert space represented by a finite set of basis vectors which were derived from the boundary conditions in our ideal experimental setup is a difficult concept for most to grasp .
Jargon, I wasn’t arguing against the use of the complex numbers, but rather that they are the natural language to express quantum in. But they are just that, a language. They represent physics, the numbers themselves don’t have any physical bearing. And yes, lol, that would be a great band name, completely agreed. It is interesting that it’s so hard to grasp this kind of mathematical structure. The consequences of non-commutativity seem to be confusing in general.
Well, AFAICT no one yet mentioned one of the weirdest possible consequences of MWI: “quantum immortality” (or quantum [frustrated] suicide: Quantum Suicide and Immortality) Instead of actually ridding us of the “nuisance” of Schrödinger’s cat, MWI arguably just makes sure he never dies. Continued superpositions justify a weird sort of “immortality” for those components of a conscious being destined to survive even the rarest of escapes from near-certain death. xxx So, sit in front of a quantum machine gun with 99.99% chance of firing a real bullet into your brain each second. Well, “you” are going to be one of “the minds” that survive, so you keep on hearing “click, click, click …” (Only versions who aren’t shot can pass judgment, compare to anthropic reasoning etc.) At least, until some inevitable (and miserable) inner decay sets in. Maybe. So, a concept meant to save the world from needing minds to make things happen, ends up perhaps making sure nothing can stop those minds from continuing to happen…
@SpinMeDown
As I understand it, extensives such as energy density are formulated in quantum mechanics not as a ratio E/V (which would be impossible since theoretically the volume of a particle is infinite) but as a bilinear (psi*)E(psi). In a unitary dynamic it loses no generality to take the norm, int (psi*)(psi) dx^3 = to be constantly 1. However, a measurement produces two or more outcomes whose norms by that definition add to 1.
In the Copenhagen Interpretation, psi is your knowledge, and you update your knowledge when you see which outcome happens, so the norm would be scaled up to 1 again.
In a Collapse Dynamics Interpretation, whichever outcome happens would take up the norm from the others, and the norm would build up to 1.
In the Many Worlds Interpretation, no such adjustment would occur. The energy before the measurement would be divvied up into the various outcomes, in proportion to probability. So the energy of what you consider to be the universe is decreasing, draining away into the rest of the multiverse.
I think this would have to mean that your universe is becoming more coarse-grained and losing information, so there wouldn’t necessarily be any information copied. However, there would be another problem with thermodynamics. The fuzziness of molecular motion, allowed by other interpretations (except Bohm), could not occur during observation, because a molecule’s paths would be separated from each other. So every material substance would become more like an ideal gas the more closely it’s observed!
That brings up another point — the Uncertainty Principle. In MWI it would hold only in aggregate throughout the multiverse. Each individual universe would have much less uncertainty, because the decisions made by observers would select among the possible position and momentum values.
I suppose there’s a way to compensate for these anomalies, to set an ad-hoc to catch an ad-hoc 😉 But to be fair, just about everything we know about physics comes rather close to a falsification.
@Serious-Gerlach: It seems that you and some other readers may be believing that the problem of interpretation will disappear when you use real functions. I seriously doubt if that is the case. The basic problem of quantum mechanics is the wave-particle duality which is an experimental fact not present in classical physics. No matter what mathematical language you use, you are not going to get around that fact. As a matter of fact some pragmatic physicists think that no interpretation is necessary!! Such a fantastic agreement of theory with experiment is unparalled in any branch of science. They say that, it is all one should demand. not that I agree with this viewpoint. BTW people are not calling diffusion equation a wave equation. What makes Schrodinger equation different from diffusion equation is precisely that “i”! You might speculate that it may be kind of diffusion in some imaginary Hilbert space!! I should also mention that Schrodinger himself tried an equation which has second order derivatives in time and space. That did not give the correct spectrum for Hydrogen atom. That is why he switched to first order in time which gave correct spectrum of hydrogen atom and was consistent with wave-particle duality in non-relativistic case. The equation with second order derivatives in space and time came back as Klein Gordon equation in quantum field theory. Relativistic version of Schrodinger equation which has both time and space derivatives of first order is the Dirac equation, still complex. But if you feel that the problem is the “i” in Schrodinger equation, then surely try the alternatives. As they say, proof of pudding is in eating!! I would caution that the present formalism has been so much successful in predicting results of experiments in physics and chemistry that you are facing a very tall order.
I would also like to add to kashyap’s point that the Schrodinger equation is NOT the wave equation in the sense of Partial Differential Equations. The Wave Equation has no dispersion, the phase velocity is equal to the group velocity. This is not true for quantum mechanics, for wave functions to encode the state’s momentum and also retain Galilei invariance, the waves must be dispersive. Without the i, the probability of a stationary state would be steadily decreasing in time and the continuity equation of probability would not hold. So you’re stuck with this dispersive “i” containing diffusion equation if you want the Born rule to hold.
@Daniel Kerr : Good point. Thanks for bringing it out. As for the debate about real vs complex algebra, I would still maintain that it is not just mathematical convenience(like in the case of electricity-magnetism) but something deeply necessary to bring out wave-particle duality. But otherwise we agree pretty much.
Kashyap, the algebra representing quantum mechanics makes no reference to numbers or vector fields at all. They are just representations of Lie Algebras, complex numbers are simply the most natural way to encode this algebra, but the numeric field used doesn’t contain any intrinsic connection to this algebra. As I said, you could replace C with the set of 2×2 matrices over R, so that each vector component is such a matrix. There are plenty of ways to keep it real while still staying true to the algebra.
@Daniel Kerr: I see your point now. I think, we may be interpreting the question of these readers about using a real wave function in a different way. The way I interpreted was that they wanted to have Schrodinger equation without “i” (to make it look like diffusion eq.) and still keep psi as a one component real object and no complex algebra. That will not work for sure. What you are suggesting is to replace psi by a two component spinor, with the second component replacing the usual imaginary part. “i” also must be replaced by a real two component column vector and multiplication should be appropriately defined to make i^2 =-1. Everything will be two dimensional. It will be clumsy but it will work!! Is this a correct and simple way of presenting your argument in a physicist’s way? I agree,just using representation theory without using vectors,you can obtain the same result. But that may be mathematician’s way of looking at quantum mechanics! I think, you will agree that complex algebra is still an easy way of doing quantum mechanics.
Kashyap, I agree that using the diffusion equation (without i) will not work at all for the reasons you and I brought up before. And yes, exactly, a 2-spinor to represent complex algebra is exactly what I meant before. It’s sloppy, but it eliminates i from the theory. Schrodinger’s equation than becomes a system of coupled PDEs. I completely agree that the complex algebra is the better way. For those who dote on it and think somehow “i” is some kind of abomination in physical theory, there are other options which highlight how it’s an element of the language of quantum mechanics and not the theory. Obviously observables being real and our operators being Hermitian guarantee that but for those still unconvinced, that’s an explicit way of showing it.
@Daniel Kerr: I’m certain the forum is not ready for a discussion about a complete set of commuting observables.