I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
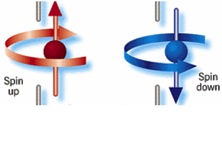The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
JimV, I answered that defense about CoE in an earlier comment. Sure, if you think that entire new universes peel off then we could imagine that conservation laws only apply in each one and so what etc. But remember, the alleged depiction of MWI is that these are not really other “universes” anyway (proponents like to complain that’s an unfair caricature of their idea, Everett did not call it MWI himself, true?) Rather, the wave function continues to evolve, it’s really all in the same universe. There is a supposed way to keep these from effectively interacting which is IMHO fallacious (roughly, due to wrongly equating optical-type “interference” with broadly causal “interference,” and the pivotal density matrix is confusingly pre-loaded with measurement-based probabilities.) So even if the interpretation is valid, it still happens in “the universe” and all the same laws are supposed to apply.
But this really isn’t continued Schrödinger evolution anyway. Just imagine a beta particle (electron) emitted towards many atoms or ions that could capture it. Each has a chance of grabbing it, so in MWI “all of them do.” But now we have a complete new electron orbital around multiple atoms. Multiple widely-separated orbitals is not a legitimate subsequent state of evolution for a single electron!
No, either the measurement is just as mysterious anyway in order to create entire new multiple effective localizations of charge, mass-energy etc, or the description fails to measure up (so to speak) to what continued SE should imply (which is the spreading of the interactibility of only one unit of mass, charge, etc over a wide area, only until it can be localized later by some kind of interaction/measurement.)
Travis,
Simply asserting that section “7 and 8 are confused and misleading talking points” is an empty assertion. As I have pointed out more than once already, when you say the correlation is not explained without non-local interactions, what you are really saying is without non-local interactions, the correlations in QM cannot be derived from a classical framework. But you have not given a reason that compels us to adopt a classical framework as the more fundamental framework. If QM is the more fundamental framework, then you simply have correlations arising from local interactions that conform to different commutation relations.
Shintaro, As I expected then. For the record, I don’t reject or even dislike ordinary QM. I’m just honest about what it is — namely, an algorithm for predicting experimental statistics which (like, say, Ptolemy’s model of the solar system) has been very successful and is undoubtedly a great achievement. At best, though, its account of what’s going on physically at the micro-level is (to use Bell’s phrase) “unprofessionally vague and ambiguous”. Your attitude seems to be that this is a good thing, and that the very desire to provide a clear physical explanation of things is outmoded, “metaphysical”, etc. If that’s right, then I guess the thing to say is that we have a philosophical disagreement: I think that it is the proper aim of physical theories to give realistic physical explanations, whereas, well, you don’t. So be it. But what I don’t understand is why it’s so important to you to be able to claim that your theory is “local”. The very notion (at least, the one at issue here) is “metaphysical” in precisely the sense that you seem to despise.
Of course, you want to switch to a different issue and talk about “locality” in the sense of local commutativity and/or no signalling. It’s uncontroversial that QM is “local” in this sense. But so is, for example, Bohmian Mechanics. Would you say that Bohmian Mechanics is therefore (like ordinary QM) local and fully compatible with relativity?
Shodan, You’ll have to explain what you mean by “classical”. I think you are trying to suggest that, by demanding a “classical framework”, I am stubbornly and irrationally insisting on a refuted, empirically inadequate physical theory (as in “classical mechanics”). But that’s just not true. I agree that classical mechanics does not provide the correct description of the micro-level, and I certainly do not restrict the scope of theories I consider to those including “F=ma”. On the other hand, what you apparently actually *mean* by “classical” in your polemical remarks is something like: the expectation that physical theories should provide clear physical explanations. But that is not something to be embarrassed about. Probably, for you, these are the same issue and you won’t really understand my point. But if you somehow became convinced at some point that, *because* F=ma doesn’t provide a correct description of electrons, it is therefore impossible in principle to explain their behavior in any clear and comprehensible way, and we must therefore give up on even trying… well, you got swindled.
Travis, when Shodan, Shintaro, or myself speak of “classical,” we’re not referring to Newtonian mechanics, we’re referring to the probability theory. Integral to Bell’s Theorem is an assignment of a classical joint probability distribution. The “classical” assumption hidden in this assignment is that one can give operators a numerical evaluation, and that evaluation will form the basis of the probability analysis that follows. This is called contextuality, and as I’ve repeatedly insist, I suggest you familiarize yourself with Kochen-Specker, which is sufficient to derive Bell’s theorem specifically in the case of spin. Bell’s theorem implicitly replaces the algebra of operators with the algebra of numbers in the probability analysis, this is the reason the inequality is not held.
Daniel et al, I’m perfectly familiar with contextuality, K-S, etc. But all of this is simply irrelevant to the question of whether locality is consistent with empirical data. Locality alone implies a Bell inequality. So we know that locality is false. Now many many other things are also true: locality implies (in certain situations) non-contextuality, locality implies determinism, the existence of joint distributions implies a Bell inequality, and on and on. But none of these other things could possibly refute the simple demonstration that locality –> Bell inequality. In my (rather extensive) experience with people who seem to share your views, the argument basically goes like this: “Bell says locality implies the inequality; but aha! — we can also derive the inequality from some other premises; so therefore there is no need to reject locality in the face of the empirical data, but we can instead reject some of those other premises.” But this is just a juvenile logical fallacy. Locality implies Bell’s inequality; experiment shows Bell’s inequality is false; so locality is false. Perhaps there are other interesting conclusions to draw as well, but doing so cannot possibly undermine something that is already established.
But this isn’t really the place to discuss this in detail. My views on Bell and nonlocality are readily available in my various papers, including the “scholarpedia.org” article on Bell’s theorem that I linked to above and which contains some discussion of these exact points. Anybody who is interested is encouraged to look at those and (as I said before) to read Bell’s own papers, which are a model of both accessibility and clarity.
I’m still hoping — perhaps in vain at this point — that we can return to the original topic and hear from Sean C about his views on the ontology of Everettism. Sean??!??
Travis, that is a rather simplistic reduction of the axioms of a formal argument to informal language. Locality as it is assumed in defining the probability distributions implies noncontextuality. Assuming locality of the operators and not of the elements sampled from the spectrum of the operators will not lead to the formulation of Bell’s inequality. You have yet to show a proof which assumes locality of the operators alone are enough to derive Bell’s inequality. I assure you that you cannot do it without assuming the noncontextuality of the detectors’ arrangements and the resulting probability distributions.
I think the sea of comments is rather polluted and if you raised your questions earlier on, I don’t see how repeating them will raise the likelihood if Sean addressing it. I too would like to know his answer.
I’ll read whatever else you guys want to say here, but I’ve said my piece and will leave it at that.
Re Neil Bates @:
July 5, 2014 at 9:46 am
“JimV, I answered that defense about CoE in an earlier comment. Sure, if you think that entire new universes peel off then we could imagine that conservation laws only apply in each one and so what etc. But remember, the alleged depiction of MWI is that these are not really other “universes” anyway …”
Thanks for the reply. Yes, that is what I think, based on the post here, and the terms “many worlds” and “multiverse”. That is, there is one wave function which evolves over time, but it causes the universe we perceive to bifurcate continuously. Or rather, that this interpretation is “correct” in the sense that it incorporates all known data in a way of thinking, or model, which makes sense to those who use it and therefore gives them a useful physical intuition about QM. (Whether the universes are “real” or not is not meaningful since we cannot interact from one to another.)
If some people mean something else by the MWI, I don’t know what that is, but wonder why they chose to use the terms “MW” and “multiverse”.
Problems with electrons choosing different orbits also seem to be non-problems to me with this interpretation since, again, the different versions cannot interact. And as Dr. Carroll said, the problem stems from the superposition principle in QM itself; as he goes on to say, the MWI (as I understand) it eliminates that conceptual problem rather than causing it. One can have superposition and understand it too (possibly incorrectly, of course).
If the particle is *always* detected entering, traveling through and exiting a single slit in a double slit experiment then why wouldn’t you be able to understand the particle travels through a single slit even when you don’t detect it?
‘Redefining Dark Matter – Wave Instead Of Particle’
http://www.science20.com/news_articles/redefining_dark_matter_wave_instead_of_particle-139771
“This opens up the possibility that dark matter could be regarded as a very cold quantum fluid”
Particles of matter travel through a single slit even when you don’t detect them.
It is the associated wave in the dark matter which passes through both.
Sean, I take issue with your equation 2. You have the apparatus, a macro system, in a superposition of states. But isn’t this what Schrodinger’s thought experiment tells us is impossible? If you don’t believe the cat is simultaneously alive *and* dead when placed in the enclosure with the radioactive source is attached, then you cannot believe in macro superpositions. But equation 2, which represents a macro superposition, is critically important to your MWI. So I have to conclude that your argument for the MWI is fatally flawed. The only fallback position I see is to assert that macro superpositions exist but decohere quickly. How quickly? Probably hugely quicker than the time it takes to write equation 2. I am interested in your response to my comment.
Wow! I didn’t know about the pilot wave theory. That Wired article is fantastic.
Could this be the nature of that wave?: http://onlyspacetime.com . All the math can be skipped, it’s easy to understand.
TrustworthyWitness,
It just keeps getting better once you realize a moving particle has an associated physical wave.
For example, take wavefunction collapse. What this is actually referring to is the cohesion between the physical particle and its associated physical wave.
The stronger the particle is detected the more it loses its cohesion with its associated wave, the less it is guided by its physical wave, the more it continues on the trajectory it was traveling.
For an analogy, consider a double slit experiment performed with a boat. The boat travels through a single slit and the bow wave passes through both. As the bow wave exits both slits it alters the direction the boat travels as it exits a single slit.
Now, in order to detect the boat, buoys are placed at the exits to the slits. As the boat exits a single slit it gets knocked around by the buoys, loses its cohesion with its bow wave and continues on the trajectory it was traveling.
What is referred to as wave function collapse is now intuitively understood to be a particle losing its cohesion with its associated physical wave.
The question then is, what waves?
Dark matter is now understood to fill what would otherwise be considered to be empty space. It is also now understood to be a very cold quantum fluid that waves.
‘Redefining Dark Matter – Wave Instead Of Particle’
http://www.science20.com/news_articles/redefining_dark_matter_wave_instead_of_particle-139771
“This opens up the possibility that dark matter could be regarded as a very cold quantum fluid”
In a double slit experiment it is the dark matter that waves. Particles of matter move through and displace the dark matter; analogous to the bow wave of a boat.
Now is the really cool part. Dark matter displaced by the particles of matter which exist in it and move through it relates general relativity and quantum mechanics.
‘Hubble Finds Ghostly Ring of Dark Matter’
http://www.nasa.gov/mission_pages/hubble/news/dark_matter_ring_feature.html
“Astronomers using NASA’s Hubble Space Telescope got a first-hand view of how dark matter behaves during a titanic collision between two galaxy clusters. The wreck created a ripple of dark matter, which is somewhat similar to a ripple formed in a pond when a rock hits the water.”
The ‘pond’ consists of dark matter. The galaxy clusters are moving through and displacing the dark matter, analogous to the bow waves of two boats which pass by each other closely. The bow waves interact and create a ripple in the water. The ripple created when galaxy clusters collide is a dark matter displacement wave.
What ripples when galaxy clusters collide is what waves in a double slit experiment; the dark matter.
Folks, it’s a cute idea there that dark matter (I’ll call it “DM”, be careful since it can also mean “density matrix”, an important math representation in QM) can be the “carrier” of the waves causing interference. However, there are various problem: one, is that the density of DM varies from point to point (it’s not the dark energy which is apparently intrinsic to space-time itself). It has been mapped and we know this from the gravitational effects. But quantum experiments are supposed to illustrate a fundamental character of matter that should not turn out differently depending on just where your lab is.
Another is that photons, as part of the EM field, already have their own EM field that in the classical limit is what does the diffracting and interfering. To add DM waves or pilot waves to that is a great kludge and confusion. Can we imagine that photons really are little BB like pellets, how would a radiating atom emit them in a particular direction when the oscillation of their orbitals is supposed to spread out in all directions (well, a shaped distribution kind of like microphone sensitivity contours.) Indeed, there isn’t a clear explanation of what causes the PWs to e.g. be emitted from a nucleus along with a decay particle etc. But at least Bohmian mechanics is easier to try to make consistent with actual statistics than MWI, because the structure of the superpositions is inherently inimical to Born probabilities.
Folks, the Milky Way’s halo is not a clump of stuff traveling along with the Milky Way.
The Milky Way is moving through and displacing the dark matter. This is why the Milky Way’s halo is lopsided.
‘The Milky Way’s dark matter halo appears to be lopsided’
http://arxiv.org/abs/0903.3802
“The emerging picture of the asymmetric dark matter halo is supported by the \Lambda CDM halos formed in the cosmological N-body simulation.”
The Milky Way’s dark matter halo is lopsided due to the matter in the Milky Way moving through and displacing the dark matter.
This is the same physical phenomenon which is occurring in a double slit experiment.
Pingback: Sciencey Stuff You May Have Missed: Week 27 « Nerdist
@kashyap vasavada July 5, 2014 at 9:22 am
That is a very astute observation, thank you for your reply and for your insight on this tough problem. Would you be able to help me a little more? What do you suppose the velocity (speed) of an electron (beta) particle is relative to that of the proton during beta decay ? Also have we considered the other electromagnetic possibilities ? If the galaxy, stars, and matter falling into black holes are spinning then would that create an overall magnetic field for a galaxy? How would you go about falsifying this approach?
I have read a little about neutrons and they do not seem to interact with the electromagnetic field. Could neutrons be a source of dark matter? Are there other types of particles emitted during beta decay that also do not interact with the electromagnetic field? Would you be able to explain conservation of charge to me?
Pingback: Sciencey Stuff You May Have Missed: Week 27 | Science-Based Life
Neil, thisisthestuff or anyone else:
I have been reading about this so called “wavefunction” or is the correct spelling “wave function”? I’m not sure I understand how it works. What exactly is the debate? From what I have seen we have some ideal physical setup and there is a superposition (that means addition right?) of multiple values of this wave thingy that satisfies the Schrodinger equation. We may have one, two or perhaps even an endless number of these funky looking solutions to something called a differential equation.
$latex
\psi_1 = \phi_1(x){e}^{-iE_1t/\hbar} \\
\psi_2= \phi_2(x){e}^{-iE_2t/\hbar} \\
\psi_3 = \phi_3(x){e}^{-iE_3t/\hbar}\\
$
Do we call each $latex \psi $ a state and is it also called an eigenstate? What is the observable that the equations above represent? Do we call the value of what we are observing an eigenvalue? If this wavefunction collapses then is it in only one of three possible states with the value associated to that particular state?
The argument I am presenting is what is considered to be wavefunction collapse is the loss if cohesive between the particle and its associated physical wave.
The stronger you detect the particle the more you destroy its cohesion with its associated wave, the less the particle is guided by its associated wave, the more the particle continues on the trajectory it was traveling.
The argument I am presenting is what is considered to be wavefunction collapse is the loss if cohesive between the particle and its associated physical wave.
The stronger you detect the particle the less the particle is guided by its associated wave, the more the particle continues on the trajectory it was traveling.
The great divide here is between instrumentalists and realists. For an instrumentalists physical models have no truth value, only utilitarian value for prediction. I call this the anti science position , I think with some justification. Science is not engineering where this kind of attitude would make sense. Science is not just about utility, in my opinion, it’s about understanding nature, even if it’s true that our scientific models are always destined to be very imperfect pictures of reality.
Deutsch sums it up nicely in the quote below, Whether or not there really are other worlds ( There is mostly certainly other histories if our cosmological models are correct) Everett got it right in terms of the relationship between the quantum and classical worlds. Bohr and company produced a lot of silly rubbish which inhibited real science with regard to understanding this relationship for over 30 years. Bohr is not the great hero in physics, he is the physics version of Lysenko , his disciples often using similar tactics to uphold the Copenhagen dogma, short of the Gulag. ( See “The Many Worlds of Hugh Everett III” by Peter Byrne)
____________________________________
” Everett was before his time, not in the sense that his theory was not timely- everybody should have adopted it in 1957, but they did not. Above all, the refusal to accept Everett is a retreat from scientific explanation. Throughout the 20 th century a great deal of harm was done in both physics and philosophy by the abdication of the original purpose of these fields: to explain the world. We got irretrievably bogged down in formalism and things were regarded as progress which are not explanatory, and the vacuum was filled by mysticism and religion and every kind of rubbish. Everett is important because he stood out against it, albeit unsuccessfully; but theories do not die and his theory will become the prevailing theory. With modifications.”
_____________________________
End Quote
@ Random dx/dt Tangent:
I commend you for your desire to understand modern physics. But there is lot of technical stuff you will have to understand. I would suggest starting from a simple book on modern physics from a public library. If there is a nearby campus where physics is taught, that will also help. I will try to answer some of the questions, but extensive discussions would need a blog by itself!
(1)In beta decay, nucleus (i) -> nucleus (f) + electron + antineutrino, the velocity of electron varies because it is a three body process involving energy and momentum conservation. It can be very high, close to velocity of light depending on the situation.
(2)For repulsion between galaxies, people have considered all sorts of electromagnetic processes. There are magnetic fields in galaxies, but they do not
help with repulsion. Dark energy is a kind of last resort!
(3) Neutrons do not have net charge. They do behave like tiny magnets though. People are doing extensive experiments with them. They are definitely not part of dark matter.
(4)Charge conservation and why charges come in integral multiples of electron charge is a great fundamental problem. There are some models based on grand unified theories. But they are not complete yet.
Hope this will help.
@Hoarse Whisperer :
I will try. But to understand it really, you will have to pick up a book on quantum theory or at least modern physics. There could be a system (say an atom) with the three separate energy levels you mention. Each of them could be an Eigen state i.e. solution of Schrodinger equation with that particular energy. You can prepare a state in the lab which is a superposition of the three states with arbitrary coefficients. According to the Born rule, the absolute square of the coefficients gives the probability of finding the energy value to be either E (1), E (2) or E (3). You will never measure energy to be any other than the three. After the measurement, the system has that particular energy and it is no longer a superposition. This is the so called collapse of wave function. Before measurement it obeys Schrodinger equation. In spite of 90 years’ debate, nobody understands what happens during the measurement. Sean is convinced that there are three universes or at least three branches of our universe where each case happens. I am not convinced. Actually I am in good company. Even as great physicist as Weinberg does not like any current interpretation. I understand he is looking for an alternative. Hope, this brief summary helps.
Bob, you can make normative statements about how science ought to be as much as you like, but if only its utility is logically/empirically justified and not its ability to produce a fundamental, ontological understanding of nature, I think we ought only operate under the assumption it is useful and not that it’s “true.” You could say I’m an empiricist like that.