I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
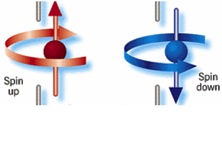The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
In the light of MWI I’m left wondering if me wondering about all the possible branches of reality actually creates more branches of reality. Not that me thinking about quantum events actually makes them occur…..unless the branches are infinitely evolving from the moment they branch out from other branches thus sooner, at the present or later resulting in me evolving the ability to control atoms and particles according to the laws of physics by mere thought. It will probably require the aid of a device of some sort, but sooner, at the present or later that technology will evolve. At the very least I expect that me mentioning the possibility of such a device here greatly increases the chances for it to come about in a more solid state in the future.*
I guess theoretically there’s a chance I’m already there, but as a matter of certainty I’m only here.
*Somewhere Deepak Chopra is channeling his arse out. My sincerest apologies, guys. 🙂
I hate playing favorites when it comes to interpretations of quantum mechanics, I think they are all a lot of fun to think about. Lets create an ethos space partitioned by the type of interpretation. If you were to measure my interpretation then you would probably find the ensemble interpretation, however, that may change in the future.
An interesting notion is to take MW’s claim of locality seriously. If so, the entanglement (or “splitting” if you will) due to a quantum event must propagate outwards at the speed of light or less (due to interactions with any mediums that get in the way, etc.). It follows then that a photon, released at the time of the event, can move away before the entanglement’s propagation ever catches up with it. That photon would have to “represent” yet another universe and has escaped the splitting of the previous, despite the event being part of it’s “universe’s” history (though we would no nothing about the outcome of that event).
Suppose though our little escapee photon manages to make it quite a ways away, evading the propagation of the splitting, but then hits a very very thick medium of some kind and gets slowed for some odd years. The propagation of entanglement then “catches up” to the photon. But what history now becomes entangled with our escapee? During the time in which the initial entanglement has propagated, many new histories were made.
I suppose the answer to that would be how MW deals with probability, or simply the history of the first photon that “catches up.” Seems intuitively messy to me though.
Not that I’m at all saying MW is out. I’m vigorously entertaining the idea. But it does lead me to weird thoughts such as this.
@Josh July 2, 2014 at 3:50 pm
I think of this interpretation along the lines of cell division. Imagine there is a world line with future and past light cones. Each event has a distinct set of possibilities at the present moment, between the two light cones. This would be analogous to a cell undergoing mitosis at each moment in time and budding off new universes with a shared history. If you deleted a chromosome from a cell and it was still able to divide then the daughter cells would inherit the genetic history of the parent cell. In your scenario the two universes would have the same history up until the point where the polarization of the photon is different or whatever observable we are measuring.
The entanglement would have happened in the shared history of both of the new daughter universes. Therefore there would not necessarily be any contradiction when the photon reaches the previously entangled partner. Do you think in the many worlds interpretation that at each moment in time a universe would be created with very low entropy and simultaneously many more universes would go immediately into a heat death?
Travis,
In your response, you tacitly assume a realist interpretation of quantum mechanics. The bread-and-butter interpretations of QM (Copenhagen and Ensemble) do not postulate any physical “collapse” process. If wavefunction collapse is not physical, then it cannot be a source of non-local properties.
See section 8 of this paper
http://arxiv.org/abs/1308.5290
If the wave function isn’t real, just tell me what your theory says is real. Then we can discuss whether the theory is local or not. Of course, Bell already proved that no matter what you say is real, the theory has to be nonlocal to agree with what’s been observed in experiments. So good luck with that.
Interpretation_MW the phase velocity of a matter wave is faster than the speed of light which may make the pilot wave theory appear nonlocal even though it does not transfer any useful information, please see the following paper . It is the group velocity of the wave that transfers information. Is it possible that the phase velocities of two different matter waves could interfere and collapse a wavefunction before the arrival of the group wave?
A question. If an observer has a box containing another observer and a box with a cat in it, does the collapse occur when the inner observer opens the box or only if both observers open their box, or does it collapse only over the box is opened to? How do these nest?
I don’t think the intuition and logic bending aspect of quantum mechanics have anything to do with “additional universes” whatever that could mean when rigorously defined. Indeed it is preposterous for a physicist to postulate something like an “additional universe” when we cannot measure any observable associated with it! To understand Quantum weirdness, you have to understand two things (1) indistinguishability. (2) the nature of non measurable quantities
So, lets start with indistinguishability. You are doing an experiment with an electron, let’s name it Fred for concreteness. You can measure an observable like momentum. Fred’s momentum is X. Five minutes later, Fred’s momentum is Y. Right, but how do you know you have just measured the momentum of Fred rather than the momentum of another electron? Don’t puzzle about it, the answer is you cannot. All electrons are completely identical to each other. And this is not like Heisenberg uncertainty where we can’t tell which is which. I mean if you actually switch out Fred in the physical equations of nature with another electron, you get the same answer for Energy, position, etc, as that of Fred. All particles are indistinguishable, a photon generated at the dawn of the Big Bang is completely identical to one freshly minted at the LHC. If “god” somehow interchanged two electrons in the universe, nothing would change (save for a minus sign), for a Boson literally nothing would change: we could not tell the difference between the universe before or after god switched Fred with Tom, a rather roguish electron that has displeased god. So it’s not always that there are two universes that exist in a superposition and the cat is dead or alive, sometimes it just doesn’t matter whether the cat is alive or dead, they are the same so far as physics is concerned. However, in many circumstances, these superposition of possible physical states is quite real, let’s have a look at that now.
So, yes, for a given one particle state the momentum measurement can return an infinite number of different measurements each with a different probability. And this is not a measurement problem, the particle is ontologically in a state where it doesn’t have definite momentum. Some states such as the finite square well force particles to NEVER be in a state of definite momentum, they are forced into this bizarre limbo. However, I don’t think this means that there are different universes in which the particle is in different states. Things we do in our universe change all of these states! If I have Fred inside an infinite square well in my universe, it I can set it up so Fred is in a superposition of an infinite number of different momentum. So if the multiverse thing is right, there is a universe for each possible momentum in which Fred has that given momentum. But if I as an experimenter alter the width of the square well, I change all the possible momentum states. So that means from my universe I can causally affect other universes, that seems to contradict the point of a universe. If universes are causually connected…they are just part of the same universe. If nothing else that breaks locality.
Much of the time, bizarre irreparable uncertainty about a certain quantity doesn’t mean there are infinite different universes in which the quantity takes a certain value. For example, conservation of particle number. Particle number is not fixed, and special relativity combined with a little QM tells us new particles can pop up at any time if there is enough energy to convert to mass, compton wavelength. Theories of quantum relativity focusing on one particle attempted by Dirac produced untamable infinities of negative energies and other monstrosities. However, if we consider that particle number can fluctuate we get valid quantum field theories of today. And the bonus is that particles minus antiparticles is still conserved thanks to complex numbers and Noether’s theorem. So when we can’t measure momentum well, and since momentum is a concept defined only by empirical observations, we shouldn’t say oh well just invent universes. We need to rethink what we MEAN by momentum, use Noether’s Theorem for that. Its not that position momentum uncertainty is a big problem with measurability, its that the concept of spacetime needs modification. Einstein did it once, and the next Einstein will have to do it again for the Plank scale. Distances and times dont really make sense down there.
The weirdness of QM isn’t something that needs to be explained away, it is a real and beautiful feature of our universe. Virtual particles and zero point energies are manifestations of quantum uncertainty, and they produce the Casimir effect (just google it). These uncertainties are not just oddities to explain away with unprovable theories, but produce real tangible effects here in our universe. It seems as though we are struggling to recover causality by inventing an infinite number of different timelines, each of which are causal. But if we can’t specify which is our universe (otherwise we know exactly how the measurement will come out), we still lose causality. Don’t worry too much about causality, locality, and all the nice logical features of physics seemingly lost to QM. Quantum field theory nicely preserves them, and in fact, all Lagrangians (and equations of nature) to date have preserved locality.
Another question I had: If the many worlds interpretation does take the wavefunction as ontological, how does MWI handle weak measurements, which allow formulation and computation of joint probability distributions of non-commuting observables?
Travis, you have a point. I tend to make a distinction between “real” as in exists, versus “realistic” as in able to be represented in the classical way like EM field theory. I don’t think reality is fully like the latter, it just isn’t “realistic”.
Entanglement: oddly, it seems harder not easier, to get a handle on that in EQM. Say we’re talking entangled photon pairs, where a measurement must be consistent like H,H or V,V. But in MWI, both outcomes happen at both locations. So where is the correlation H:H and V:V? The math doesn’t describe the actual polarization of either photon by itself, it’s a mysterious heuristic way to say that if one shows one way, the other does to. There isn’t even a “realistic” way to describe even the WF of either photon before detection (ie, as a definite polarization, not to be confused with what happens in detection. Normally, we *can* prepare a photon to have a specific polarization, that’s how we can guarantee detection if we want to.)
Dan, weak measurements are IMHO a good point. Also, what about Renninger negative result experiments (Renninger negative-result experiment): one detector registers “no photon” but there is remaining time for the wave function to continue toward another detector etc. So now, the *negative* measurement causes the WF to be “redistributed” rather than fully “collapsed” at a given location. How does that pan out in MWI? Furthermore, we are in the habit of taking detectors for granted as perfect. But what about reliability issues? If the detector registers “yes” falsely etc, what sort of complicated situation does that amount to?
BTW, I don’t think the resolution of Schrödinger’s cat has anything to do with people *looking* at it, either. I think that muons, nuclei etc. really just decay at definite moments. Also, photons really are absorbed by specific atoms, and so on. This is an interactive notion, neither involving “observers” nor intrusion of unusual special collapse-inducing events as in some objective-collapse theories. That’s my intuition, it’s hard to rigorously justify.
Kai, I see your point. However, note a paradigmatic simple case, the photon split by half-silver toward two detectors. If you imagine a “realistic” WF, it has to either go “poof” when either detector *legitimately* registers a hit, or “continue evolving” (which really isn’t: now we have the full energy of the photon at two locations, instead of a WF describing the original amount as spread out over space.) That really is “weirdness” at heart. Oh I don’t want to see it “explained away” either, it should be accepted as the way our universe is, like it or not …
But Princess, about non-locality: I think it has to be an actual influence, even if it doesn’t transfer what we call useful information. That is so the other result matches the first one, which *can’t occur as a result of independent properties* (the whole point of Bell inequalities, correct me if wrong.) If “not independent” then something has to connect them, and of course it’s not just previous real traits either as in Bertlemann’s socks.
Schrödinger’s Cat, as traditionally described, is not a very good model.
In order to properly construct Schrödinger’s Cat thought experiment, we need to imagine a box with a sleeping (or awake cat) and a rubber band gun attached to the lid. In order to determine if the cat is awake or asleep, we have to open the lid, which triggers the rubberband gun. Maybe it wakes the cat, maybe it misses. At this point, we can close the lid and open it again and will obtain the same result.
It is only when we put enough energy into the system to reset the rubberband gun and close the lid for a long enough time that the cat might fall asleep that we can obtain a different result. Both measurement and reset of the system require energy and energy changes the results.
What if probability waves really is what it’s all about? In order to measure the wave, we have to construct a scenario where only a limited set of choices is allowed. Similar to looking at a single frame of a movie or taking a flash photograph of action. We are only viewing one moment. We are not freezing the probability curve, only our view. The probability curves do do not disappear. There is no decoherence.
In this scenario, the future is only ever a set of possibilities, while the past is the only thing that can be determined. This may very well be why the arrow of time flows in one direction. Knowing the past, we can calculate our way toward present, but no matter what we know about position/velocity of a particle, we can only calculate probabilities of where it will go, what it will do in the future. The calculation only works one way.
I put this wonderful and fantastic theory into the “extraordinary claims” department. And we know what Carl Sagan has said about that. Will such evidence ever be produced in sufficient quality and quantity, or will it ultimately rest on faith?
$latex i\hbar \frac{\partial \Psi }{\partial t}= -\frac{\hbar^2}{2m}\bigtriangledown^2 \Psi $
What values of $latex \Psi $ satisfies the above equation?
What about $latex \Psi $ in the following equation?
$latex \hbar \frac{\partial \Psi }{\partial t}= -\frac{\hbar^2}{2m}\bigtriangledown^2 \Psi $
Instead of debating interpretations should we instead be debating if the i in the Schrodinger equation is needed?
Schrodinger’s Mistress,
The i is definitely needed. Without the i, there is no unitary evolution. You would get crazy probabilities, and no correct predictions of what we observe.
Travis,
You continue to assert an incorrect understanding of Bell’s theorem, which states that no local theory of hidden variables can reproduce the predictions of quantum mechanics. If no hidden variables are postulated, there is no reason to insist any non-locality that isn’t already in classical mechanics. This is a very basic point.
What are real in quantum mechanics are experimental phenomena. Quantum mechanics tells us the probabilities of observing possible results of an experiment. We do so by expanding a state vector in the relevant basis and squaring the resulting coefficients.
Shodan, Travis is right. BT does indeed say that no local HVs can reproduce all of QM. But that doesn’t mean you can forget about there being non-local effects. The phenomena are correlated in such a way, that if they were independent, that could not happen. That means that *no local properties* can explain the strong correlations (like both detectors getting the same result, despite arbitrary random shifting around of pair properties), which means that something non-local has to explain them (if you want explanations at all.) If there were no non-local connections, then the entangled measurements just wouldn’t be able to show the strong correlations (too statistically independent.) Your second paragraph doesn’t account for entangled states, it is an outline of single-state statistics.
BTW, you are right about the “i” – I note the irony, of referring to unitary evolution and “probabilities” together, regarding its purpose.
Bell’s Theorem definitely doesn’t require non-local effects unconditionally. The phenomena of measuring both particles are not independent in entangled states, they’re correlated. One such example of an interpretation that is local but lacks hidden variables is as follows, consider this classical thought experiment to frame the interpretation: If we put one red ball and one blue ball in a basket, mixed it up, then had two people grab one ball without looking and walked lightyears apart, we wouldn’t argue that something non-local has to occur so that when one sees his/her ball is red, the other sees his/her is blue.
This isn’t exactly analogous as I could have looked at the ball at any time along the way including while I grabbed it, my ignorance isn’t physical in origin but rather lazy. However, in an EPR type experiment, you can measure the spin at any distance from the emission source up until the original interaction. The correlation occurs during the particle creation step, and the spin is completely unaffected/interacted with until measurement. There’s no reason to believe that the distance we choose to measure the spin at matters, so we’re left to conclude that the correlation occurred locally when the particle pair was created.
It’s not that one particle’s seemingly independent state is correlated with another’s, not at all, it’s that there’s one overall state in which the spins of the two particles along the same axis are always correlated. In the former case we’re asking what determines, once we measure particle 1’s spin, how particle 2 will correlate as it has to. Any such solution will seem non-local. In the latter we realize the correlation between spin values, regardless of what they are in a given experiment, is fundamental to the state itself and its initial formation, it’s just a matter of sampling it.
Daniel, that is not at all how entangled correlations work. You are describing the classical situation called “Bertlemann’s socks”, which works with initial correlation. But the strong correlations can’t involve that, since they must create correlations for arbitrarily oriented detector pairs. That can’t be handled by prior real properties or LHVs. You need to read up on entanglement and understand that. I am not an expert on this myself, but at least cover the bases so to speak.
“But the strong correlations can’t involve that, since they must create correlations for arbitrarily oriented detector pairs.”
That’s the argument. But then again, the argument is also that the probability distributions we get from one detector must appear to be independent of the the orientation of – or even the existence of – the other detector. If this wasn’t the case, faster than light communication would be trivial. Bell states that local hidden variables are dependent upon the orientation for the one detector not affecting the measurement of the other. I’m still trying to find a good explanation of how one can say that it both affects it and gives the same probability distribution (any help would be appreciated).
It’s pretty sad to see the way you act as if MWI is “the truth” and mock people for not “accepting it”. In reality it is you who refuse to look at what nature and science is telling us (so far). The preferred basis problem has not been solved *at all* as is pointed out by several commenters here. They are also the posts with clearly the most upvotes.
This is a trend I’ve witnessed in your blog over and over. Everytime someone mentions the basis and born rule problem, you refuse to adress it, because you have no answer.
Instead you continue insisting that you have found the truth and that your scifi interpretation is the REAL Science and that people that disagree is “in denial”.
Why can’t you just accept that currently there is no interpretation or theory that gives us an answer and the only thing we know for sure is that it’s none of the current interpretations in their current form. INCLUDING EQM.
Neil,
Both you and Travis are wrong. By insisting the strong correlations unique to quantum mechanics must imply non-local affects, you are tacitly assuming these correlated observables are described by classical degrees of freedom. This is just as bad as assuming hidden variables. Instead, the fact that some observables don’t commute means correlations emerging from local interactions can be stronger than in classical physics. You are simply assuming reality has some fundamental classical component, and then inferring spooky action as a result. In actuality, quantum entanglement is just as natural in the context of the laws of quantum mechanics as the correlation between Bertlmann’s socks.
Neil, if you believe I am mistaken, feel free to clear up such issues in detail. I’d prefer leading with an argument then with a comment on credentials.
That said, the correlation is in the state of the particles. When the detectors interact with the particles, their pointer states will in turn correlate with the state of the particles. That’s what a measurement is (ideally). With both detectors along the same axis, the correlation of the original state will be preserved. However, as you rotate the detectors’ orientation relative to one another, this correlation with the initial state decreases. When perpendicular, all information is lost as a z +1/2 state could register as a y +1/2 or y -1/2 with equal probabilities. This is a geometric effect. The correlation between detectors is due to the correlation of spin operators with each other. Each pair of spin operators that forms the orthonormal basis for spin operators has no correlation (as spin z +1/2 could be correlated with y +1/2 or y -1/2 with equal probability), while each operator has perfect correlation with itself. Any spin operators that are not perpendicular to each other have some intrinsic correlation.
The correlation between the detectors is at best reflecting the original state’s correlation. Off-angle correlations are a result of the embedding of this state in the geometry of the SU(2) spin group. There are no other sources of correlations here, so I will ask you to qualify what you mean by “strong” correlations if they are not initial correlations or the result of joint probability distributions of non-commuting operators (which is a geometric contribution).
I’m unclear what MWI says about actions or experiments that can have multiple (more than 2) outcomes or that have probabilities other than 50:50? For example, consider an experiment whose outcome has a statistical bell-shaped curve? Or the collapse of the wave function of an electron, which has a non-zero probability of appearing anywhere in the universe. What does MWI say will happen?