I have often talked about the Many-Worlds or Everett approach to quantum mechanics — here’s an explanatory video, an excerpt from From Eternity to Here, and slides from a talk. But I don’t think I’ve ever explained as persuasively as possible why I think it’s the right approach. So that’s what I’m going to try to do here. Although to be honest right off the bat, I’m actually going to tackle a slightly easier problem: explaining why the many-worlds approach is not completely insane, and indeed quite natural. The harder part is explaining why it actually works, which I’ll get to in another post.
Any discussion of Everettian quantum mechanics (“EQM”) comes with the baggage of pre-conceived notions. People have heard of it before, and have instinctive reactions to it, in a way that they don’t have to (for example) effective field theory. Hell, there is even an app, universe splitter, that lets you create new universes from your iPhone. (Seriously.) So we need to start by separating the silly objections to EQM from the serious worries.
The basic silly objection is that EQM postulates too many universes. In quantum mechanics, we can’t deterministically predict the outcomes of measurements. In EQM, that is dealt with by saying that every measurement outcome “happens,” but each in a different “universe” or “world.” Say we think of Schrödinger’s Cat: a sealed box inside of which we have a cat in a quantum superposition of “awake” and “asleep.” (No reason to kill the cat unnecessarily.) Textbook quantum mechanics says that opening the box and observing the cat “collapses the wave function” into one of two possible measurement outcomes, awake or asleep. Everett, by contrast, says that the universe splits in two: in one the cat is awake, and in the other the cat is asleep. Once split, the universes go their own ways, never to interact with each other again.
And to many people, that just seems like too much. Why, this objection goes, would you ever think of inventing a huge — perhaps infinite! — number of different universes, just to describe the simple act of quantum measurement? It might be puzzling, but it’s no reason to lose all anchor to reality.
To see why objections along these lines are wrong-headed, let’s first think about classical mechanics rather than quantum mechanics. And let’s start with one universe: some collection of particles and fields and what have you, in some particular arrangement in space. Classical mechanics describes such a universe as a point in phase space — the collection of all positions and velocities of each particle or field.
What if, for some perverse reason, we wanted to describe two copies of such a universe (perhaps with some tiny difference between them, like an awake cat rather than a sleeping one)? We would have to double the size of phase space — create a mathematical structure that is large enough to describe both universes at once. In classical mechanics, then, it’s quite a bit of work to accommodate extra universes, and you better have a good reason to justify putting in that work. (Inflationary cosmology seems to do it, by implicitly assuming that phase space is already infinitely big.)
That is not what happens in quantum mechanics. The capacity for describing multiple universes is automatically there. We don’t have to add anything.
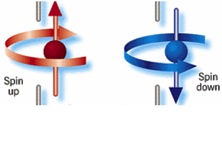The reason why we can state this with such confidence is because of the fundamental reality of quantum mechanics: the existence of superpositions of different possible measurement outcomes. In classical mechanics, we have certain definite possible states, all of which are directly observable. It will be important for what comes later that the system we consider is microscopic, so let’s consider a spinning particle that can have spin-up or spin-down. (It is directly analogous to Schrödinger’s cat: cat=particle, awake=spin-up, asleep=spin-down.) Classically, the possible states are
“spin is up”
or
“spin is down”.
Quantum mechanics says that the state of the particle can be a superposition of both possible measurement outcomes. It’s not that we don’t know whether the spin is up or down; it’s that it’s really in a superposition of both possibilities, at least until we observe it. We can denote such a state like this:
(“spin is up” + “spin is down”).
While classical states are points in phase space, quantum states are “wave functions” that live in something called Hilbert space. Hilbert space is very big — as we will see, it has room for lots of stuff.
To describe measurements, we need to add an observer. It doesn’t need to be a “conscious” observer or anything else that might get Deepak Chopra excited; we just mean a macroscopic measuring apparatus. It could be a living person, but it could just as well be a video camera or even the air in a room. To avoid confusion we’ll just call it the “apparatus.”
In any formulation of quantum mechanics, the apparatus starts in a “ready” state, which is a way of saying “it hasn’t yet looked at the thing it’s going to observe” (i.e., the particle). More specifically, the apparatus is not entangled with the particle; their two states are independent of each other. So the quantum state of the particle+apparatus system starts out like this:
(“spin is up” + “spin is down” ; apparatus says “ready”) (1)
The particle is in a superposition, but the apparatus is not. According to the textbook view, when the apparatus observes the particle, the quantum state collapses onto one of two possibilities:
(“spin is up”; apparatus says “up”)
or
(“spin is down”; apparatus says “down”).
When and how such collapse actually occurs is a bit vague — a huge problem with the textbook approach — but let’s not dig into that right now.
But there is clearly another possibility. If the particle can be in a superposition of two states, then so can the apparatus. So nothing stops us from writing down a state of the form
(spin is up ; apparatus says “up”)
+ (spin is down ; apparatus says “down”). (2)
The plus sign here is crucial. This is not a state representing one alternative or the other, as in the textbook view; it’s a superposition of both possibilities. In this kind of state, the spin of the particle is entangled with the readout of the apparatus.
What would it be like to live in a world with the kind of quantum state we have written in (2)? It might seem a bit unrealistic at first glance; after all, when we observe real-world quantum systems it always feels like we see one outcome or the other. We never think that we ourselves are in a superposition of having achieved different measurement outcomes.
This is where the magic of decoherence comes in. (Everett himself actually had a clever argument that didn’t use decoherence explicitly, but we’ll take a more modern view.) I won’t go into the details here, but the basic idea isn’t too difficult. There are more things in the universe than our particle and the measuring apparatus; there is the rest of the Earth, and for that matter everything in outer space. That stuff — group it all together and call it the “environment” — has a quantum state also. We expect the apparatus to quickly become entangled with the environment, if only because photons and air molecules in the environment will keep bumping into the apparatus. As a result, even though a state of this form is in a superposition, the two different pieces (one with the particle spin-up, one with the particle spin-down) will never be able to interfere with each other. Interference (different parts of the wave function canceling each other out) demands a precise alignment of the quantum states, and once we lose information into the environment that becomes impossible. That’s decoherence.
Once our quantum superposition involves macroscopic systems with many degrees of freedom that become entangled with an even-larger environment, the different terms in that superposition proceed to evolve completely independently of each other. It is as if they have become distinct worlds — because they have. We wouldn’t think of our pre-measurement state (1) as describing two different worlds; it’s just one world, in which the particle is in a superposition. But (2) has two worlds in it. The difference is that we can imagine undoing the superposition in (1) by carefully manipulating the particle, but in (2) the difference between the two branches has diffused into the environment and is lost there forever.
All of this exposition is building up to the following point: in order to describe a quantum state that includes two non-interacting “worlds” as in (2), we didn’t have to add anything at all to our description of the universe, unlike the classical case. All of the ingredients were already there!
Our only assumption was that the apparatus obeys the rules of quantum mechanics just as much as the particle does, which seems to be an extremely mild assumption if we think quantum mechanics is the correct theory of reality. Given that, we know that the particle can be in “spin-up” or “spin-down” states, and we also know that the apparatus can be in “ready” or “measured spin-up” or “measured spin-down” states. And if that’s true, the quantum state has the built-in ability to describe superpositions of non-interacting worlds. Not only did we not need to add anything to make it possible, we had no choice in the matter. The potential for multiple worlds is always there in the quantum state, whether you like it or not.
The next question would be, do multiple-world superpositions of the form written in (2) ever actually come into being? And the answer again is: yes, automatically, without any additional assumptions. It’s just the ordinary evolution of a quantum system according to Schrödinger’s equation. Indeed, the fact that a state that looks like (1) evolves into a state that looks like (2) under Schrödinger’s equation is what we mean when we say “this apparatus measures whether the spin is up or down.”
The conclusion, therefore, is that multiple worlds automatically occur in quantum mechanics. They are an inevitable part of the formalism. The only remaining question is: what are you going to do about it? There are three popular strategies on the market: anger, denial, and acceptance.
The “anger” strategy says “I hate the idea of multiple worlds with such a white-hot passion that I will change the rules of quantum mechanics in order to avoid them.” And people do this! In the four options listed here, both dynamical-collapse theories and hidden-variable theories are straightforward alterations of the conventional picture of quantum mechanics. In dynamical collapse, we change the evolution equation, by adding some explicitly stochastic probability of collapse. In hidden variables, we keep the Schrödinger equation intact, but add new variables — hidden ones, which we know must be explicitly non-local. Of course there is currently zero empirical evidence for these rather ad hoc modifications of the formalism, but hey, you never know.
The “denial” strategy says “The idea of multiple worlds is so profoundly upsetting to me that I will deny the existence of reality in order to escape having to think about it.” Advocates of this approach don’t actually put it that way, but I’m being polemical rather than conciliatory in this particular post. And I don’t think it’s an unfair characterization. This is the quantum Bayesianism approach, or more generally “psi-epistemic” approaches. The idea is to simply deny that the quantum state represents anything about reality; it is merely a way of keeping track of the probability of future measurement outcomes. Is the particle spin-up, or spin-down, or both? Neither! There is no particle, there is no spoon, nor is there the state of the particle’s spin; there is only the probability of seeing the spin in different conditions once one performs a measurement. I advocate listening to David Albert’s take at our WSF panel.
The final strategy is acceptance. That is the Everettian approach. The formalism of quantum mechanics, in this view, consists of quantum states as described above and nothing more, which evolve according to the usual Schrödinger equation and nothing more. The formalism predicts that there are many worlds, so we choose to accept that. This means that the part of reality we experience is an indescribably thin slice of the entire picture, but so be it. Our job as scientists is to formulate the best possible description of the world as it is, not to force the world to bend to our pre-conceptions.
Such brave declarations aren’t enough on their own, of course. The fierce austerity of EQM is attractive, but we still need to verify that its predictions map on to our empirical data. This raises questions that live squarely at the physics/philosophy boundary. Why does the quantum state branch into certain kinds of worlds (e.g., ones where cats are awake or ones where cats are asleep) and not others (where cats are in superpositions of both)? Why are the probabilities that we actually observe given by the Born Rule, which states that the probability equals the wave function squared? In what sense are there probabilities at all, if the theory is completely deterministic?
These are the serious issues for EQM, as opposed to the silly one that “there are just too many universes!” The “why those states?” problem has essentially been solved by the notion of pointer states — quantum states split along lines that are macroscopically robust, which are ultimately delineated by the actual laws of physics (the particles/fields/interactions of the real world). The probability question is trickier, but also (I think) solvable. Decision theory is one attractive approach, and Chip Sebens and I are advocating self-locating uncertainty as a friendly alternative. That’s the subject of a paper we just wrote, which I plan to talk about in a separate post.
There are other silly objections to EQM, of course. The most popular is probably the complaint that it’s not falsifiable. That truly makes no sense. It’s trivial to falsify EQM — just do an experiment that violates the Schrödinger equation or the principle of superposition, which are the only things the theory assumes. Witness a dynamical collapse, or find a hidden variable. Of course we don’t see the other worlds directly, but — in case we haven’t yet driven home the point loudly enough — those other worlds are not added on to the theory. They come out automatically if you believe in quantum mechanics. If you have a physically distinguishable alternative, by all means suggest it — the experimenters would love to hear about it. (And true alternatives, like GRW and Bohmian mechanics, are indeed experimentally distinguishable.)
Sadly, most people who object to EQM do so for the silly reasons, not for the serious ones. But even given the real challenges of the preferred-basis issue and the probability issue, I think EQM is way ahead of any proposed alternative. It takes at face value the minimal conceptual apparatus necessary to account for the world we see, and by doing so it fits all the data we have ever collected. What more do you want from a theory than that?
I agree with you Neil, that you can’t say CoE doesn’t matter if you can’t observe its violation, but unobservable sub-sets of state should be considered real.
What I do disagree with you about is whether Everett does violate CoE. I think the problem stems from having internalized Copenhagen, and seeing a measurement of a quantum system as making the quantum superposition “go away” so now the electron has one definite momentum, so to get to a state where it also has a different momentum you need to clone the electron or otherwise break conservation laws. But that’s not what’s happening in this view. In this view, the electron no more has one definite momentum after measurement than it did before. The only thing that changed is that the distribution of possible momenta is entangled/correlated with the distribution of possible momenta measurements of whatever system interacts with the electron.
If an electron having a distribution of possible locations, momenta, etc prior to measurement does not violate conservation laws, then in Everett it doesn’t do so after measurement because measurement is not a special operation.
Note that, it can’t be just “the same stuff divided into regions that don’t interact.” The WF of a particle reflects a certain amount of momentum, of mass-energy in that wave packet. If I for any reason postulate say, two such packets (due to alternate histories, one where the whole particle was seen to go one way, and another one where the particle went the other way), then those two packets represent a total of “two” mass units rather than a distribution of one unit into e.g. a doubly-peaked wave packet. And so on.
I’m now 72 and that means there are a lot of “me’s” out there. One of them may have won a Nobel prize of some sort. What I want to know is why I’m not in that quantum slice. Why am “I” in this one and not the one where I’ve won a Nobel prize, and how do “I” get there?
@Jen
“How could a state become ‘unavailable’ to me unless it occurred in a separate Universe?”
A good question! Depends on what we mean by “universe”, in part. For instance, consider a black hole. Nothing that occurs inside the event horizon can possibly have any effect on you outside watching the black hole — this is what “event horizon” means. So would you say then that the inside of a black hole is another universe? Well, you *could*, and that’s fine. And I think this is the perspective from which Everett got its unfortunate name “Many Worlds” that at first glance implies the universe cloning whole copies of itself on every quantum interaction.
But another way to look at it is that if you look at the metric (mathematical description of the geometry) of all of space-time, including the black holes with their event horizons and singularities, regions of space expanding away from other regions faster than light, etc, you can call that whole thing a “universe” described by a single metric, but some sub-sets of that universe can’t communicate with each other.
Similarly, you *could* say the alternate outcome of quantum events represents another universe, because you can’t interact with it. Or, you could say that it’s all one universe described by one wavefunction, only sub-sets of states described by that wavefunction are inconsistent and so don’t interact.
@Neil:
Everett takes QM for granted, yes, and entanglement is a feature of it that was inferred before it was witnessed. Entanglement is when two particles interact in such a way that they must have a correlated state (e.g. exchanging momentum, so the sum of their delta-p must be 0), but have not interacted with the rest of the universe in such a way that their state must correlate with it. It’s no different than superposition of states in a one-particle system, just now it’s two particles. Or more. In Everett all that changes is that entanglement isn’t magically zapped away by measurement. Superposition still exists. All the possibilities for the combined system are still present as a single wavefunction, which does not “collapse” to one. You see it as meaning there’s now two wavefunctions describing two electrons for double the energy, but that’s not it, there’s still one wavefunction describing all possibilities, so no CoE violation.
The role/meaning of probability in Everett is a real problem, which Sean readily admits.
@CB: No, because if we accept MWI then the behavior appropriate to one entire particle happens “here” and also “there”, when that is not really intelligible as the working meaning of superposition under normal terms – when it’s a scheme to describe spreading out and chances of interaction for a single particle.
Plus have the number of streams appropriate to the number of superpositions (however broken down, which is another problem) then you have no basis for Born probabilities. Sure, Sean et al admits it’s a – nice candor but isn’t coming close to making it credible. The scheme just doesn’t work, and you can even think about things like what is “E” field (not energy) in space from all those possible locations? What keeps that “separated”? Referring to “entanglement” is just hand-waving, it doesn’t explain anything, it’s just what we call the correlation of actual exclusive type outcomes – there’s no “there” there, we don’t know what goes on underneath. Try to work on the double-peak versus two particle wave issue.
@CB:
“Everett is local, though, and maybe he counts that in its favor, but it doesn’t come across that way.”
Well, I’d like to hear first from Sean what he even takes the ontology/beables of the Everettian theory to be. I don’t think you can possibly say that it is local or nonlocal prior to settling that issue. What would it even *mean* to claim that the theory is “local”, if what the theory posits (as physically real) is (exclusively) a moving point on the unit sphere in Hilbert space, or a complex-valued field in some 3N-dimensional (where N is either really big or infinite) space? “Locality” is the idea that physical influences — in ordinary three-dimensional physical space — never propagate faster than the speed of light. If, according to your theory, there is no such three-dimensional physical space (and ipso facto no physical influences propagating around in it at all) it is at best misleading and empty to say the theory is “local”.
BTW, the fact that an incoherent (disorderly) superposition is 1. called a “mixture” because some people think it is “equivalent” or should be and 2. the statistics created *by measurements* applied to the IS are “classical”, doesn’t mean the IS really is a mixture or that explains it behaving like a mixture. Again, we get localization “statistics” out of a coherent double-slit experiment too. An incoherent superposition is just that, both states in a disorderly distribution, and only when a measurement or perhaps it is certain interactions occur, does the state sometimes fall into one outcome, and other times into the other outcome. The “mixture” is not intrinsically there due to decoherence, it is built up from varying patterns of measurement outcomes.
@CB:
I agree that there are situations where there is no conscious observer involved e.g. quantum mechanical reactions were going on in stars long before any conscious being emerged. But that does not answer the main question about arbitrariness. To be more explicit, suppose a professor asks a graduate student to perform a QM expt. Next morning, if the student gets up early and does the expt. then the universe has large number of extra copies including copies of the poor graduate student which were not around the previous day. If he sleeps late and does not do the expt., then there are no more copies. This looks absurd and metaphysical at best. If you are saying that there are already copies made in heavens before the expt. and the student is merely picking a particular branch that is probably worse. If the various branches of the universe are only in our mind that is also bad. Every other student has to get the same results. All the branches of the universe have to combine at the end of the expt. to give probabilistic QM result! Copenhagen interpretation, which talks about our limited knowledge of the QM system, is any day more sensible! How about an engineering student who is doing classical expt.? My main point is that MWI just increases the number of universes without solving any problem, QM calculations are exactly same as before. MWI is completely arbitrarily cooked up to get out of the difficulty that QM has proved impossible to understand after some 90 years of debate! I am surprised that nobody brought up this point in the numerous debates which Sean had with religious scholars and philosophers. I am sympathetic with metaphysics in religious context, but not in physics context.
It’s interesting to me that there is a whole cadre of cosmologists wondering how even ONE universe can be created, while Sean is creating – how many – ? every second?
Travis Norsen’s paper on Bell is worth a read. See J.S. Bell’s Concept of Local Causality on arXiv:
“Many textbooks and commentators report that Bell’s theorem refutes the possibility (suggested especially by Einstein, Podolsky, and Rosen in 1935) of supplementing ordinary quantum theory with additional (“hidden”) variables that might restore determinism and/or some notion of an observer-independent reality. On this view, Bell’s theorem supports the orthodox Copenhagen interpretation. Bell’s own view of his theorem, however, was quite different…”
IMHO the many-worlds interpretation and the Copenhagen interpretation is unscientific woo peddled by quacks who tell lies, who castigate people like Joy Christian, and studiously ignore work by the likes of Aephraim Steinberg and Jeff Lundeen et al. Beware Sean, because that unscientific woo is a dead man walking. It won’t last much longer. Don’t be left high and dry championing it.
wow 2 thumbs up !… and 4 thumbs down…
but I`ll take what I can get. I know what i’m suggesting is not high end physics,
but surely it still makes sense to check our most basic rational assumptions, especially where a theory e.g. time and how it seems to be directional at a classical scale and non-directional at a quantum level, seems to end up with so many fractures of supposition, and alternative theories, at the higher levels.
for those thumbs up, and thumbs down, (and anyone else) i’ve put what i’m suggesting we might consider as related to the…
Time travel, Worm hole, billiard ball’ paradox, Timelessly. (re Paul Davies- New scientist article) for example
https://www.youtube.com/watch?v=Wc5cRGOGIEU
(hope it’s ok to post a link)
mm
John D, I have long been curious about such alternatives to any standard QM interpretation, that say there is neither a real problem nor do we need many “worlds.” You are right to be suspicious of CI, which doesn’t really get under the hood; and MWI, which is fallacious in its framing, and has a structure directly antithetical to the Born probabilities – which fans try to evade with too-clever-by-half handwaving. Yet I don’t see convincing explanations. Joy Christian’s point AFAICT is more about explaining entanglement without unusual non-local influences (and I’m still not persuaded altho it invokes some unfamiliar applications of math), than it is about the basic problem of say the half-silver split photon and how it might end up in one detector on the other, but not both; etc. What is the answer to that basic problem, including the Born probabilities?
can someone explain how EQM doesn’t violate mass/energy conservation? Each time the universe splits, you are presumably doubling everything…Sean says this is taken care of by “superposition of states”, but the quantum states (spin, polarization etc) are bits of information, and do not have any energy or mass associated with them…for example: not only you have to consider the two possible spin states, but also the electron that contains the information about the spin.
also, there is the assumption that multiple states (worlds) exist at the same time (superposition). Doesn’t it make more sense that only one of the states really exists and we simply don’t know which ones it it? And once we make the measurement, one of the possible states is bound to be found. And then we can say that all along, the spin was what we measured it to be…but we just didn’t know it for sure.
I find this old post from Chad Orzel very sensible & clarifying: http://scienceblogs.com/principles/2008/11/20/manyworlds-and-decoherence/
How does Orzel’s explanation fit here? Is it an example of the Copenhagen interpretation?
Wizard, good questions, but the spin can’t “have been that all along” – it’s hard to go through explaining just why in brief, but if you check out some guides you will see. As for Orzel, well he doesn’t overcome the basic flaws that I and others have noted.
Travis,
Without hidden variables, QM is only non-local in the same way classical mechanics (CM) is non-local. I.e. Correlations exist between space-like separated regions. Matching socks are an example of non-local correlation. Sure, QM permits stronger correlations than CM, but it is still a local theory unless you introduce hidden variables.
So this is why you like philosophy — so you can believe in supernatural worlds without any evidence.
Quantum mechanics has been confirmed many times in many ways, but there is not a shred of evidence for many worlds.
Sorry, I wasn’t asking if Orzel’s views are correct. I don’t have the expertise to have an opinion on that. I was just asking how his post fits into the various views discussed here — is it an example of the Copenhagen interpretation, the ensemble interpretation, or what?
JW, Orzel was outlining (not quite as a proselytizer, he seems laid back about which is true) this same sort of decoherence-driven splitting into many “worlds” consisting of continuing superpositions. Copenhagen basically says, we just can’t represent what goes on between measurements, and ensemble is roughly saying we can’t represent what goes on in single cases, “we can only talk about” collections of what they usually call “similarly-prepared states.”
One alternative to MWI that imagines a specific real sequence of events is de Broglie/Bohm mechanics, with particles at specific locations and guided by special “pilot waves.” They claim that can replicate standard QM results, but actually: a deterministic theory cannot in principle simulate genuine randomness, for if you recreate the same initial conditions in the former, the outcome must literally be *the same outcome* and not just the same “chances.” Also, I can’t see how dBB handles random decay of apparently structureless, all-identical muons (nor MWI, for that matter – they aren’t even interacting with anything else, and instead of specific alternative paths, it’s a continuum of increasing chance to decay!)
Sure, Sean is cute. But I think that there are just too many universes!! He infers from the fact that a superposition is represented as one vector in a Hilbert space that it splits into two unvierses. But that the state is represented by one vector means there is only one thing there (even if on a product space).
You know, if Many-Worlds were true, you could have two universes splitting off at different times, i.e. when you do the experiment in universe 1 it takes 10 sec. to get the result [x-spin up>, but it takes 20 sec. in universe2 to get the result [x-spin down>.
I don’t think the basis problem has been satisfactorily solved. Selected bases would, in some time frame, creep into other bases, and eventually a system would observe another system to be in a superpostion.
In half the universes I agree with you, in the other half I disagree with you.
Shodan,
No, ordinary (textbook/orthodox) QM is not local. The measurement axioms (the “collapse postulate”) in particular violate locality. This was pointed out already in 1935 by E, P, and R. This is why it’s a standard talking point for Everettianism that, by getting rid of the collapse postulate and retaining only the unitary, schroedinger evolution, their theory is local. But as I have tried to suggest, it is not really even clear what that claim is supposed to mean when the theory doesn’t seem to postulate any local beables, i.e., any physically real “stuff” (like particles or fields or *something*) in ordinary physical space.
Hopefully Sean will find time to explain what he understands the Everettian ontology to be.
I’d like to point out that Everett himself never said the universe as universe splits. His claim is that the observer (state) splits or branches inside the universal wave function. This is not a trivial matter, since it does not mean that a whole new universe has to pop into existence at every quantum interaction. See:http://www.amazon.com/The-Many-Worlds-Hugh-Everett/dp/0199552274
Folks, sorry to say that indeed “the universe” effectively does have to split (not to be confused with how the enthusiasts try to spin it.) Say I have a quantum experiment with photons, and say 34:66 (sic, not 1:2) chance that will cause an apple to either stay put, or be ejected in a particular direction. Furthermore, our club election has been based on the outcome, for Neil or Cyndi. The moment arrives, and “I” (LOL) see the apple sitting there. Everything from then on has to be consistent with that: people taking pictures of it even far away, talking about it, me reaching out and grabbing it, and so on (yes, I know, after that moment even more “universes” are created in turn per each little fluctuation, but this sets a minimum base for the mess.) That keeps going into what people write about, the entire flow of history works from there: I am club President, Cyndi is not, and so on.
But the “superposition in which the apple was propelled away” is also still real, according to our mystical wizards (because a theory designed to explain *what really happens* – well that’s what normal ones do – ends up predicting *something other than what really happens* (in any meaningful empirical sense.) In that “world” the apple is speeding away, Cyndi is selected President of our club, and an entire different history must go along with that: the club newsletter, speeches to visitors, maybe Cyndi meets someone to marry she otherwise wouldn’t, etc.
BTW, what physical process actually keeps that “other apple” – yes, its entire original mass-energy also at other locations – from hitting stuff in “my world”? Linear evolution? Then how can we ever know of the other streams at all, before or after the “measurements” – that is, any evidence at all of superpositions period? And what does coherence (orderliness) of the superposition have to do, intrinsically, with literal physical interaction?
Well let’s be generous and suppose then, there were indeed two basic streams directly connected to the quantum event affecting the apple. So now we have that irritating 34:66 probability to deal with. Well, the structure of continuing superpositions is inherently inimical to frequentist representation of the outcomes according to Born probability. And the defenses of how MWI can do this are regularly pilloried as being circular arguments, and so it goes.
Folks, did you really think this stuff through?