Each year, the 14th of March is celebrated by scientifically-minded folks for two good reasons. First, it’s Einstein’s birthday (happy 135th, Albert!). Second, it’s Pi Day, because 3/14 is the closest calendrical approximation we have to the decimal expansion of pi, π =3.1415927….
Both of these features — Einstein and pi — are loosely related by playing important roles in science and mathematics. But is there any closer connection?
Of course there is. We need look no further than Einstein’s equation. I mean Einstein’s real equation — not E=mc2, which is perfectly fine as far as it goes, but a pretty straightforward consequence of special relativity rather than a world-foundational relationship in its own right. Einstein’s real equation is what you would find if you looked up “Einstein’s equation” in the index of any good GR textbook: the field equation relating the curvature of spacetime to energy sources, which serves as the bedrock principle of general relativity. It looks like this:
It can look intimidating if the notation is unfamiliar, but conceptually it’s quite simple; if you don’t know all the symbols, think of it as a little poem in a foreign language. In words it is saying this:
(gravity) = 8 π G × (energy and momentum).
Not so scary, is it? The amount of gravity is proportional to the amount of energy and momentum, with the constant of proportionality given by 8πG, where G is a numerical constant.
Hey, what is π doing there? It seems a bit gratuitous, actually. Einstein could easily have defined a new constant H simply be setting H=8πG. Then he wouldn’t have needed that superfluous 8π cluttering up his equation. Did he just have a special love for π, perhaps based on his birthday?
The real story is less whimsical, but more interesting. Einstein didn’t feel like inventing a new constant because G was already in existence: it’s Newton’s constant of gravitation, which makes perfect sense. General relativity (GR) is the theory that replaces Newton’s version of gravitation, but at the end of the day it’s still gravity, and it has the same strength that it always did.
So the real question is, why does π make an appearance when we make the transition from Newtonian gravity to general relativity?
Well, here’s Newton’s equation for gravity, the famous inverse square law:
It’s actually similar in structure to Einstein’s equation: the left hand side is the force of gravity between two objects, and on the right we find the masses m1 and m2 of the objects in question, as well as the constant of proportionality G. (For Newton, mass was the source of gravity; Einstein figured out that mass is just one form of energy, and upgraded the source of gravity to all forms of energy and momentum.) And of course we divide by the square of the distance r between the two objects. No π’s anywhere to be found.
It’s a great equation, as physics equations go; one of the most influential in the history of science. But it’s also a bit puzzling, at least philosophically. It tells a story of action at a distance — two objects exert a gravitational force on each other from far away, without any intervening substance. Newton himself considered this to be an unacceptable state of affairs, although he didn’t really have a good answer:
That Gravity should be innate, inherent and essential to Matter, so that one body may act upon another at a distance thro’ a Vacuum, without the Mediation of any thing else, by and through which their Action and Force may be conveyed from one to another, is to me so great an Absurdity that I believe no Man who has in philosophical Matters a competent Faculty of thinking can ever fall into it.
But there is an answer to this conundrum. It’s to shift one’s focus from the force of gravity, F, to the gravitational potential field, Φ (Greek letter “phi”), from which the force can be derived. The field Φ fills all of space, taking some specific value at every point. In the vicinity of a single body of mass M, the gravitational potential field is given by this equation:
This equation bears a close resemblance to Newton’s original one. It depends inversely on the distance, rather than the distance squared, because it’s not the gravitational force directly; the force is given by the derivative (slope) of the field, which turns 1/r into 1/r2.
That’s nice, since we’ve replaced the spookiness of action at a distance with the pleasantly mechanical notion of a field filling all of space. Still no π’s, though.
But our equation only tells us what happens when we have a single body with mass M. What if we have many objects, each creating its own gravitational field, or for that matter a gas or fluid spread throughout some region? Then we need to talk about the mass density, or the amount of mass per each little volume of space, conventionally denoted ρ (Greek letter “rho”). And indeed there is an equation that relates the gravitational potential field to an arbitrary mass density spread throughout space, known as Poisson’s equation:
The upside-down triangle is the gradient operator (here squared to make the Laplacian); it’s a fancy three-dimensional way of saying how the field is changing through space (its vectorial derivative). But even more exciting, π has now appeared on the right-hand side! Why is that?
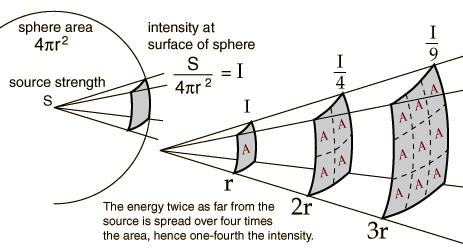
There is a technical mathematical explanation, of course, but here is the rough physical explanation. Whereas we were originally concerned (in Newton’s equation or the first equation for Φ) with the gravitational effect of a single body at a distance r, we’re now adding up all the accumulated effects of everything in the universe. That “adding up” (integrating) can be broken into two steps: (1) add up all the effects at some fixed distance r, and (2) add up the effects from all distances. In that first step, all the points at some distance r from any fixed location define a sphere centered on that location. So we’re really adding up effects spread over the area of a sphere. And the formula for the area of a sphere, of course, is:
Seems almost too trivial, but that’s really the answer. The reason π comes into Poisson’s equation and not Newton’s is that Newton cared about the force between two specific objects, while Poisson tells us how to calculate the potential as a function of a matter density spread all over the place, and in three dimensions “all over the place” means “all over the area of a sphere” and then “adding up each sphere.” (We add up spheres, rather than cubes or whatever, because spheres describe fixed distances from the point of interest, and gravity depends on distance.) And the area of a sphere, just like the circumference of a circle, is proportional to π.
So then what about Einstein? Back in Newtonian gravity, it was often convenient to use the gravitational potential field, but it wasn’t really necessary; you could always in principle calculate the gravitational force directly. But when Einstein formulated general relativity, the field concept became absolutely central. The thing one calculates is not the force due to gravity (indeed, there’s a sense in which gravity isn’t really a “force” in general relativity), but rather the geometry of spacetime. That is fixed by the metric tensor field, a complicated beast that includes as a subset what we call the gravitational potential field. Einstein’s equation is directly analogous to Poisson’s equation, not to Newton’s.
So that’s the Einstein-Pi connection. Einstein figured out that gravity is best described by a field theory rather than as a direct interaction between individual bodies, and connecting fields to localized bodies involves integrating over the surface of a sphere, and the area of a sphere is proportional to π. The whole birthday thing is just a happy accident.
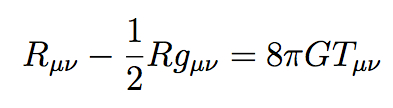
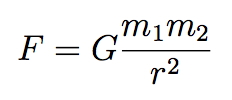
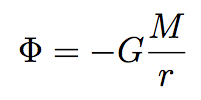
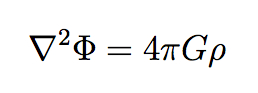
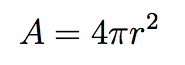
The problem about how Newtonian Physics says gravity acts with an action at a distance and Einsteins version of gravity doesn’t, has troubled me for a long time. I believed I understood why Newtons version says this, but I have always been unclear as to why Einsteins version does not. Then I still seem to be confused as to how one would know that changing an r to an r^2 would change this. Then I don’t see anything in the equation that describes how long it would take gravity to influence other objects.
It is discomforting that Newton felt so strongly about action at a distance being a problem, but he never heard of quantum physics. To me it is easy to accept the possibility, when there are so many examples of it occurring in that field. Then Einstein didn’t really agree with any of the founding principles of the theory either, and tried to fight against it with the EPR Paradox. I would hate to find that a lot of the reason behind this was just because Einstein created the speed of light limit.
@2:
The CGS (Gaussian) system of units avoids the four pi in Coulomb’s law, but then it has to show up in Maxwell’s equations. SI defines epsilon zero such that a four pi is needed in Coulomb’s law, but is avoided in Maxwell’s Equations. I presume that since more people work with Maxwell’s equations, the SI choice is more convenient for the most people.
The fact that pi must show up in one place or the other is a clue about the underlying mathematics relating these equations.
See
http://en.wikipedia.org/wiki/Gaussian_units#Maxwell.27s_equations
G was probably too well established for the SI folks to play this sort of game anyway, but it also seems likely that more people work with Newton’s Law of Gravitation than work with General Relativity, so where the pi ends up is still a convenient choice for the most people.
As I understand it, the h or h bar distinction is largely a matter of convenience. Does one prefer to measure angular velocity in cycles/second or radians /second? AFAIK there’s nothing deeper there than the basic fact that one full rotation is a rotation of two pi radians.
“…relationship in it’s own right…”
Sean! Apostrophe misuse is a hanging offence!
A question for anyone who disapproved of my post above – can you determine the exact centre of a sphere?
It amounts to an infinite regression down the number Pi in my view. That is “infinity” inwards as a basis for a solid theory.
Give my book a read, or help me out with an obvious answer if there is one.
I hope to get an answer from a physicist here to my simple question above.
I am not sure what insult I gave in my declined post above, but that’s the essential issue I am identifying.
You see, that is infinite regression and not a finite point as the basis for G.R. Am I correct? Don’t worry about the consequences – we can discuss those if you would like, but my supposition is correct is it not?
Any takers, or only voters?
Pingback: Links 3/15/14: Ides of March | naked capitalism
GR is a non-local, non-linear theory. Non-local meaning that the effective potential at a given point, is ill-defined (as a result of SR). Newtonian gravity (in gravitational potential form) is local and linear.
It has been shown that Newtonian gravity can be reformulated as curved space with non-curved time … but GR requires both space and time to be curved … this is because GR is a generalization of SR, where time and space are dependent rather than independent.
Because of this, gravitational lensing, which exists in both theories (as a result of curvature in both) results in a 2x difference in light bending near the Sun (not surprising because in natural units in a Minkowski diagram, light is 45 degrees relative to both the space and time axis … implying equal codependence in any subsequent equation that has both as independent variables).
The speed of gravity propagation comes about, because of gravitational wave theory, which was originally found by linear approximation of GR (which also leads to the correspondence equation between GR and Newtonian gravitational theory) … a wave equation can be derived, with a “wave speed” in the usual location … which is “C”.
It is because of the “simultaneity” problem in SR, that GR is non-local … two distinct space-time events have an observer dependent relationship, so the effective potential at a point is similarly dependent.
Marcus Morgan … I liked your comment, because it shows a mind grasping for the intangible. Indeed, if space-time in inherently non-local, because of the “simultaneity” problem in SR, then the center of a sphere, in physical space (where time is implied), is going to be inherently non-local too. And infinite series summed or not, abound.
My passions also lean toward the paradoxical ideas of math and physics more than any practical calculation or experimental determination (not that those are unimportant). That two different sets of ideas, can in fact lead to the same equation, or that two different equations can lead to the same calculated result … is itself a non-locality of a more general kind. So I am an anti-Feynman by nature … because he was a calculational whiz … and eschewed the philosophy of physics because it is far more slippery than pedagogy would admit to.
BTW – the value of Pi, in the case of a relativistically rotating sphere, at its equator (relative to the axis of spin) is smaller than normal. Math and physics work together like the melody and lyrics of a good song, but they are not the same species, in spite of what Pythagoras or Euclid said … just the same genera.
In regards to Marcus Morgan’s question: “can you determine the exact centre of a sphere?”
Are you asking for the geometrical center of the sphere, or the philosophical center, or the practical center? No need to answer my question, the question is rhetorical. I know where you want to go.
Pingback: Baskerville Post
Pingback: Einstein and Pi | Sean Carroll | Mark Solock Blog
Thanks William – it seems that the centre of a sphere is infinitely uncertain, and I think I understand your reference to the divide between “assumed” linearity and actual measurement. Measurement is an approximation, in fact 22/7 is a neat fraction even though irreducible, and any fraction can be inserted into an equation, but that is an approximation.
In my view the logic of measurement precedes the assumptions we make in measuring, including avoidance of uncertainty at a spherical centre and its implications for G.R. You should have a look at my free book to see if you like my reworked framework for measurement to remove the misunderstanding, or schism, you identify. I explain how science uses approximations by its Uncertainty Principle, and other matters.
Math is a tool used by humans to describe or define nature, like words. It has a scope to it bounded by the human capacity to reason. I don’t get concerned about schisms because that’s humans – prone to error and polarization.
Famos “No need to answer my question, the question is rhetorical. I know where you want to go.”
I will play mind reader and assume you think I am promoting God as behind the whole shebang? that would explain the 48 votes against my post with my site address http://thehumandesign.net Unfortunately I misunderstood the hijacking of the word Design by the Intelligent Design crowd when I wrote the first edition of my book several years ago. I see continually at blogs that as soon as the word appears there is a huge knee jerk reaction. Is it that fear Faros? Or do you have a point to make with your riddle?
Its a sad turn of events when people see a word and judge a book by its cover. I learned about the error of that in childhood. I like the word Design, it applies to the laws of nature. Whether I believe in God or not is none of your concern, but God is not the subject of the book if that’s the point to your strange riddle.
Thanks for so much, Sean.
But you dismiss e=mc2 as “a pretty straightforward consequence of special relativity” and I have never found a satisfactory explanation of how one gets from the equations of special relativity to e-mc2. I once audited a course from Bethe who covered all this, but his explanation was too deep into tensors for me. And it’s not enough to call it a constant of integration. My web searches have yielded nothing more satisfying.
Could you, or someone, point me at a better explanation/derivation?
Thanks again,
John Weil
Einstein’s original derivation had of E=Mc^2 … was based on dual light pulses emitted in opposite directions by some mass … this derivation was controversial. Henri Poincare had the right formula 5 years earlier, in regards to radiation pressure. What distinguished Einstein was he had a more general framework that applied to more situations than just EM fields. Prior even to 1900, others had derived similar formulas based on other principles.
The fact is, relativity theory, like Newtonian theory or quantum theory, doesn’t actually tell you what mass/inertia is. GR theory was the first to explain why gravitational mass and inertial mass are equal … so that aspect of mass can’t be deduced from SR theory alone. SR theory only provides a framework in which other theories can be developed, either emendations of earlier classical theories, or new ones … it is axiomatically independent in the same way the parallel postulate is independent in Euclidean geometry. And the Higgs field/particle while SR relativistic, is not conceptually compatible with GR theory. Mass/energy is exogenous cause relative to both SR and GR theory, though GR theory accounts for the effects better than any other theory.
Marcus Morgan,
“I am not sure what insult I gave in my declined post above.”
Answer: You’re shamelessly plugging your pseudo-science book like a filthy 18th century whore. Boom goes the dynamite.
Oh Meh, we (didn’t) chat in a previous thread because you could not understand my sentence structure “at all” but then proceeded to judge it nonetheless. So, is this another judgment of the same kind, or do you understand the issue?
Meh, what hope do we have for progress if people cannot even exchange ideas – at all in your case, or at least with some civility?
I am struggling for reasons for your outburst as you provide none – just a judgmental opinion without facts. Are you upset at being caught out for your self-contradiction in the last thread? If that’s the reason for your startling illogicality now, let it go. How did you find the exchange I had with William – sentence structure-wise?
Have a read of the book and tell me what is pseudo-scientific about it? That would be a start. It follows a self-consistent logical thread that identifies well established facts and fits them into a new framework. It is reasoning, which can be applied effectively to anything. If you don’t do that, I will just have to write you off as a stalker or a troll or whatever the expression is for the internet. Give it a go, its a good book, not one to burn.
Excellent coverage William, I rarely read an easy use of concepts without jargon or math, but Sean does well sometimes. If I may – the way around these ‘issues’ is to restructure but preserve observation – confirmed observation. The first step is to reinstate the void – continuous space and time both extending equably in and out (meaning ‘in’ to Pi infinitely within mass itself). Mass occupies it and has its own spaces and times measured as discrete motions & positions, including field exchanges at constant light speed by a field mechanism to use the inverse relation of position and motion on emission and absorption by particles, to adjust for particle motion by distributing its position across the surface at one end while also at light speed at a front end. Create a quantum model of exchange in a void.
Remove G.R. and its two dimensional Hologram from the FLRW Metric, which is bizarre, but preserve its equations in a void, because having discrete space and time capacities within a continuum of a space and time void provides all the distortions theorised and measured in G.R. – in a void. They are discrete and individual, requiring Transformations to reconcile, even in a void. This is achievable also by the same field mechanisms that adjust for particle motion.
Higgs is a belated attempt at filling a gap of “weight” . Higgs preserves curved Spacetime rather than a mechanical interface in a void (yet again achievable by a field mechanism for both electromagnetism and gravitation). If G.R. is preserved, it just compresses for relative weights, and mass needs ‘weight’ in the first place in a belated attempt by Higgs. Do you know much about particle colliders and whether in search for a specific product they can repeatedly smash masses together until they get “something like it” after a great deal of smashing?
The answer specifically for gravitation may be to unify particles and their fields into one particle-field the unifies particle inertia and field force into a simple equivalence from a two-part mechanism (again). As you see, I have a mechanical view in a void that preserves all G.R. and S.R measurements but dispenses with their shortcomings. Have a flip through my book, its free and not a self-promotion – just new original ideas. I can’t help the fact that they are my ideas – the point is to raise them when relevant to a topic, which is the purpose of these sites for those that want to use them.
INTERESTING
Please Ref:
http://www.stefanides.gr/Html/piquad.htm
http://www.stefanides.gr/Html/QuadCirc.htm
http://www.stefanides.gr/Html/theo_circle.htm
Regards from Athens,
Panagiotis Stefanides
http://www.stefanides.gr
Thanks Panagiotis, I had a look – trying to square a circle got me thinking about the irrationality of Pi.
I enjoyed the article in tone and substance, but was most taken by your use of the Hubble “Deep Field South” as a background decoration…for me, it is the most significant image of our time…a panorama of galaxies, not just stars!
Your clear prose has me thinking “Yeah, I got this” at the end of expository posts like this one. Then I try to explain it to my 19 y.o. nephew, and I get stuck about 5 words in.
Clearly, I need to go a layer deeper to get enough context to form my own gestalt to use as the basis for an explanation to others.
When available for future posts like this, if you have any “FMI” links to share, it would be most gratefully appreciated! (Even if it’s in the form of “as any undergrad physics text would show …”)
Thanks for ticking my mind to make me WANT to dig deeper!
I took a stab at an answer to the several requests to explain why it’s 8 and not 4 in Sean’s version of the Einstein Field Equation, but kept falling down explanation ratholes involving the value of the stress-energy-momentum tensor T_{\mu \nu}.
While awaiting a future more boring post explaining it, one could hopefully not-too-snarkily say that the reason that 8 is in there is because while Sean set both c and \Lambda to 1 in writing the EFE at the top, he chose a system of units which does not do the same to 8 \pi G, as Baez does here:
http://math.ucr.edu/home/baez/einstein/node6a.html
which explains the same relationship in a slightly different (and arguably more boring 🙂 ) way. Following the link back to “[Baez’s] formulation of Einstein’s equation (2)” reveals some of the ratholes…
I think the question is a good one, but the answer isn’t easy to make both terse and accessible.
Pingback: Física y poesía | Versvs
So why not G bar?
I don’t recall the name of the specific physicist but he explained Einstein’s gravity equation as “reading left to right it’s space-time telling matter how to move and reading right to left it’s matter telling space-time how to curve,” which seems appropriate given E=mc^2! Einstein was a friend of Carl Jung, I wonder if he ever considered the possibility that the birthday thing could be some kind of Jungian Synchronicity rather than just a happy accident . . .