November 2013

This year we give thanks for an idea that establishes a direct connection between the concepts of “energy” and “information”: Landauer’s Principle. (We’ve previously given thanks for the Standard Model Lagrangian, Hubble’s Law, the Spin-Statistics Theorem, conservation of momentum, effective field theory, the error bar, and gauge symmetry.)

Landauer’s Principle states that irreversible loss of information — whether it’s erasing a notebook or swiping a computer disk — is necessarily accompanied by an increase in entropy. Charles Bennett puts it in relatively precise terms:

Any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information bearing degrees of freedom of the information processing apparatus or its environment.

The principle captures the broad idea that “information is physical.” More specifically, it establishes a relationship between logically irreversible processes and the generation of heat. If you want to erase a single bit of information in a system at temperature T, says Landauer, you will generate an amount of heat equal to at least

where k is Boltzmann’s constant.

This all might come across as a blur of buzzwords, so take a moment to appreciate what is going on. “Information” seems like a fairly abstract concept, even in a field like physics where you can’t swing a cat without hitting an abstract concept or two. We record data, take pictures, write things down, all the time — and we forget, or erase, or lose our notebooks all the time, too. Landauer’s Principle says there is a direct connection between these processes and the thermodynamic arrow of time, the increase in entropy throughout the universe. The information we possess is a precious, physical thing, and we are gradually losing it to the heat death of the cosmos under the irresistible pull of the Second Law.

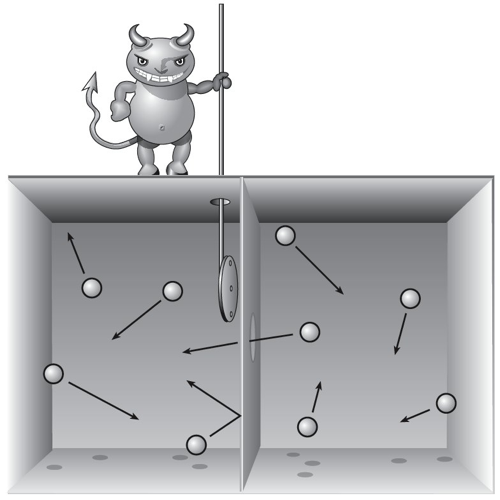
The principle originated in attempts to understand Maxwell’s Demon. You’ll remember the plucky sprite who decreases the entropy of gas in a box by letting all the high-velocity molecules accumulate on one side and all the low-velocity ones on the other. Since Maxwell proposed the Demon, all right-thinking folks agreed that the entropy of the whole universe must somehow be increasing along the way, but it turned out to be really hard to pinpoint just where it was happening.

The answer is not, as many people supposed, in the act of the Demon observing the motion of the molecules; it’s possible to make such observations in a perfectly reversible (entropy-neutral) fashion. But the Demon has to somehow keep track of what its measurements have revealed. And unless it has an infinitely big notebook, it’s going to eventually have to erase some of its records about the outcomes of those measurements — and that’s the truly irreversible process. This was the insight of Rolf Landauer in the 1960’s, which led to his principle.

A 1982 paper by Bennett provides a nice illustration of the principle in action, based on Szilard’s Engine. Short version of the argument: imagine you have a piston with a single molecule in it, rattling back and forth. If you don’t know where it is, you can’t extract any energy from it. But if you measure the position of the molecule, you could quickly stick in a piston on the side where the molecule is not, then let the molecule bump into your piston and extract energy. The amount you get out is (ln 2)kT. You have “extracted work” from a system that was supposed to be at maximum entropy, in apparent violation of the Second Law. But it was important that you started in a “ready state,” not knowing where the molecule was — in a world governed by reversible laws, that’s a crucial step if you want your measurement to correspond reliably to the correct result. So to do this kind of thing repeatedly, you will have to return to that ready state — which means erasing information. That decreases your phase space, and therefore increases entropy, and generates heat. At the end of the day, that information erasure generates just as much entropy as went down when you extracted work; the Second Law is perfectly safe.

The status of Landauer’s Principle is still a bit controversial in some circles — here’s a paper by John Norton setting out the skeptical case. But modern computers are running up against the physical limits on irreversible computation established by the Principle, and experiments seem to be verifying it. Even something as abstract as “information” is ultimately part of the world of physics.

Bit of old news here — well, the existence of the Moon is extremely old news, but even this new result is slightly non-new. But it was new to me.

Ice Cube is a wondrously inventive way of looking at the universe. Sitting at the South Pole, the facility itself consists of strings of basketball-sized detectors reaching over two kilometers deep into the Antarctic ice. Its purpose is to detect neutrinos, which it does when a neutrino interacts with the ice to create a charged lepton (electron, muon, or tau), which in turn splashes Cherenkov radiation into the detectors. The eventual hope is to pinpoint very high-energy neutrinos coming from specific astrophysical sources.

For this purpose, it’s the muon-creating neutrinos that are your best bet; electrons scatter multiple times in the ice, while taus decay too quickly, while muons give you a nice straight line. Sadly there is a heavy background of muons that have nothing to do with neutrinos, just from cosmic rays hitting the atmosphere. Happily most of these can be dealt with by using the Earth as a shield — the best candidate neutrino events are those that hit Ice Cube by coming up through the Earth, not down from the sky.

It’s important in this game to make sure your detector is really “pointing” where you think it is. (Ice Cube doesn’t move, of course; the detectors find tracks in the ice, from which a direction is reconstructed.) So it would be nice to have a source of muons to check against. Sadly, there is no such source in the sky. Happily, there is an anti-source — the shadow of the Moon.

Cosmic rays rain down on the Earth, creating muons as they hit the atmosphere, but we expect a deficit of cosmic rays in the direction of the Moon, which gets in the way. And indeed, here is the map constructed by Ice Cube of the muon flux in the vicinity of the Moon’s position in the sky.

There it is! I can definitely make out the Moon.

Really this is a cosmic-ray eclipse, I suppose. We can also detect the Moon in gamma rays, and the Sun in neutrinos. It’s exciting to be living at a time when technological progress is helping us overcome the relative poverty of our biological senses.

Peter Coles has issued a challenge: explain why dark energy makes the universe accelerate in terms that are understandable to non-scientists. This is a pet peeve of mine — any number of fellow cosmologists will recall me haranguing them about it over coffee at conferences — but I’m not sure I’ve ever blogged about it directly, so here goes. In three parts: the wrong way, the right way, and the math.

The Wrong Way

Ordinary matter acts to slow down the expansion of the universe. That makes intuitive sense, because the matter is exerting a gravitational force, acting to pull things together. So why does dark energy seem to push things apart?

The usual (wrong) way to explain this is to point out that dark energy has “negative pressure.” The kind of pressure we are most familiar with, in a balloon or an inflated tire, pushing out on the membrane enclosing it. But negative pressure — tension — is more like a stretched string or rubber band, pulling in rather than pushing out. And dark energy has negative pressure, so that makes the universe accelerate.

If the kindly cosmologist is both lazy and fortunate, that little bit of word salad will suffice. But it makes no sense at all, as Peter points out. Why do we go through all the conceptual effort of explaining that negative pressure corresponds to a pull, and then quickly mumble that this accounts for why galaxies are pushed apart?

So the slightly more careful cosmologist has to explain that the direct action of this negative pressure is completely impotent, because it’s equal in all directions and cancels out. (That’s a bit of a lie as well, of course; it’s really because you don’t interact directly with the dark energy, so you don’t feel pressure of any sort, but admitting that runs the risk of making it all seem even more confusing.) What matters, according to this line of fast talk, is the gravitational effect of the negative pressure. And in Einstein’s general relativity, unlike Newtonian gravity, both the pressure and the energy contribute to the force of gravity. The negative pressure associated with dark energy is so large that it overcomes the positive (attractive) impulse of the energy itself, so the net effect is a push rather than a pull.

This explanation isn’t wrong; it does track the actual equations. But it’s not the slightest bit of help in bringing people to any real understanding. It simply replaces one question (why does dark energy cause acceleration?) with two facts that need to be taken on faith (dark energy has negative pressure, and gravity is sourced by a sum of energy and pressure). The listener goes away with, at best, the impression that something profound has just happened rather than any actual understanding.

The Right Way

The right way is to not mention pressure at all, positive or negative. For cosmological dynamics, the relevant fact about dark energy isn’t its pressure, it’s that it’s persistent. It doesn’t dilute away as the universe expands. And this is even a fact that can be explained, by saying that dark energy isn’t a collection of particles growing less dense as space expands, but instead is (according to our simplest and best models) a feature of space itself. The amount of dark energy is constant throughout both space and time: about one hundred-millionth of an erg per cubic centimeter. It doesn’t dilute away, even as space expands.

Given that, all you need to accept is that Einstein’s formulation of gravity says “the curvature of spacetime is proportional to the amount of stuff within it.” (The technical version of “curvature of spacetime” is the Einstein tensor, and the technical version of “stuff” is the energy-momentum tensor.) In the case of an expanding universe, the manifestation of spacetime curvature is simply the fact that space is expanding. (There can also be spatial curvature, but that seems negligible in the real world, so why complicate things.)

So: the density of dark energy is constant, which means the curvature of spacetime is constant, which means that the universe expands at a fixed rate.

The tricky part is explaining why “expanding at a fixed rate” means “accelerating.” But this is a subtlety worth clarifying, as it helps distinguish between the expansion of the universe and the speed of a physical object like a moving car, and perhaps will help someone down the road not get confused about the universe “expanding faster than light.” (A confusion which many trained cosmologists who really should know better continue to fall into.)

The point is that the expansion rate of the universe is not a speed. It’s a timescale — the time it takes the universe to double in size (or expand by one percent, or whatever, depending on your conventions). It couldn’t possibly be a speed, because the apparent velocity of distant galaxies is not a constant number, it’s proportional to their distance. When we say “the expansion rate of the universe is a constant,” we mean it takes a fixed amount of time for the universe to double in size. So if we look at any one particular galaxy, in roughly ten billion years it will be twice as far away; in twenty billion years (twice that time) it will be four times as far away; in thirty billion years it will be eight times that far away, and so on. It’s accelerating away from us, exponentially. “Constant expansion rate” implies “accelerated motion away from us” for individual objects.

There’s absolutely no reason why a non-scientist shouldn’t be able to follow why dark energy makes the universe accelerate, given just a bit of willingness to think about it. Dark energy is persistent, which imparts a constant impulse to the expansion of the universe, which makes galaxies accelerate away. No negative pressures, no double-talk.

The Math

So why are people tempted to talk about negative pressure? As Peter says, there is an equation for the second derivative (roughly, the acceleration) of the universe, which looks like this:

(I use a for the scale factor rather than R, and sensibly set c=1.) Here, ρ is the energy density and p is the pressure. To get acceleration, you want the second derivative to be positive, and there’s a minus sign outside the right-hand side, so we want (ρ + 3p) to be negative. The data say the dark energy density is positive, so a negative pressure is just the trick.

But, while that’s a perfectly good equation — the “second Friedmann equation” — it’s not the one anyone actually uses to solve for the evolution of the universe. It’s much nicer to use the first Friedmann equation, which involves the first derivative of the scale factor rather than its second derivative (spatial curvature set to zero for convenience):

Here H is the Hubble parameter, which is what we mean when we say “the expansion rate.” You notice a couple of nice things about this equation. First, the pressure doesn’t appear. The expansion rate is simply driven by the energy density ρ. It’s completely consistent with the first equation, as they are related to each other by an equation that encodes energy-momentum conservation, and the pressure does make an appearance there. Second, a constant energy density straightforwardly implies a constant expansion rate H. So no problem at all: a persistent source of energy causes the universe to accelerate.

Banning “negative pressure” from popular expositions of cosmology would be a great step forward. It’s a legitimate scientific concept, but is more often employed to give the illusion of understanding rather than any actual insight.