Kim Boddy and I have just written a new paper, with maybe my favorite title ever.
Can the Higgs Boson Save Us From the Menace of the Boltzmann Brains?
Kimberly K. Boddy, Sean M. Carroll
(Submitted on 21 Aug 2013)The standard ΛCDM model provides an excellent fit to current cosmological observations but suffers from a potentially serious Boltzmann Brain problem. If the universe enters a de Sitter vacuum phase that is truly eternal, there will be a finite temperature in empty space and corresponding thermal fluctuations. Among these fluctuations will be intelligent observers, as well as configurations that reproduce any local region of the current universe to arbitrary precision. We discuss the possibility that the escape from this unacceptable situation may be found in known physics: vacuum instability induced by the Higgs field. Avoiding Boltzmann Brains in a measure-independent way requires a decay timescale of order the current age of the universe, which can be achieved if the top quark pole mass is approximately 178 GeV. Otherwise we must invoke new physics or a particular cosmological measure before we can consider ΛCDM to be an empirical success.
We apply some far-out-sounding ideas to very down-to-Earth physics. Among other things, we’re suggesting that the mass of the top quark might be heavier than most people think, and that our universe will decay in another ten billion years or so. Here’s a somewhat long-winded explanation.
A room full of monkeys, hitting keys randomly on a typewriter, will eventually bang out a perfect copy of Hamlet. Assuming, of course, that their typing is perfectly random, and that it keeps up for a long time. An extremely long time indeed, much longer than the current age of the universe. So this is an amusing thought experiment, not a viable proposal for creating new works of literature (or old ones).
There’s an interesting feature of what these thought-experiment monkeys end up producing. Let’s say you find a monkey who has just typed Act I of Hamlet with perfect fidelity. You might think “aha, here’s when it happens,” and expect Act II to come next. But by the conditions of the experiment, the next thing the monkey types should be perfectly random (by which we mean, chosen from a uniform distribution among all allowed typographical characters), and therefore independent of what has come before. The chances that you will actually get Act II next, just because you got Act I, are extraordinarily tiny. For every one time that your monkeys type Hamlet correctly, they will type it incorrectly an enormous number of times — small errors, large errors, all of the words but in random order, the entire text backwards, some scenes but not others, all of the lines but with different characters assigned to them, and so forth. Given that any one passage matches the original text, it is still overwhelmingly likely that the passages before and after are random nonsense.
That’s the Boltzmann Brain problem in a nutshell. Replace your typing monkeys with a box of atoms at some temperature, and let the atoms randomly bump into each other for an indefinite period of time. Almost all the time they will be in a disordered, high-entropy, equilibrium state. Eventually, just by chance, they will take the form of a smiley face, or Michelangelo’s David, or absolutely any configuration that is compatible with what’s inside the box. If you wait long enough, and your box is sufficiently large, you will get a person, a planet, a galaxy, the whole universe as we now know it. But given that some of the atoms fall into a familiar-looking arrangement, we still expect the rest of the atoms to be completely random. Just because you find a copy of the Mona Lisa, in other words, doesn’t mean that it was actually painted by Leonardo or anyone else; with overwhelming probability it simply coalesced gradually out of random motions. Just because you see what looks like a photograph, there’s no reason to believe it was preceded by an actual event that the photo purports to represent. If the random motions of the atoms create a person with firm memories of the past, all of those memories are overwhelmingly likely to be false.
This thought experiment was originally relevant because Boltzmann himself (and before him Lucretius, Hume, etc.) suggested that our world might be exactly this: a big box of gas, evolving for all eternity, out of which our current low-entropy state emerged as a random fluctuation. As was pointed out by Eddington, Feynman, and others, this idea doesn’t work, for the reasons just stated; given any one bit of universe that you might want to make (a person, a solar system, a galaxy, and exact duplicate of your current self), the rest of the world should still be in a maximum-entropy state, and it clearly is not. This is called the “Boltzmann Brain problem,” because one way of thinking about it is that the vast majority of intelligent observers in the universe should be disembodied brains that have randomly fluctuated out of the surrounding chaos, rather than evolving conventionally from a low-entropy past. That’s not really the point, though; the real problem is that such a fluctuation scenario is cognitively unstable — you can’t simultaneously believe it’s true, and have good reason for believing its true, because it predicts that all the “reasons” you think are so good have just randomly fluctuated into your head!
All of which would seemingly be little more than fodder for scholars of intellectual history, now that we know the universe is not an eternal box of gas. The observable universe, anyway, started a mere 13.8 billion years ago, in a very low-entropy Big Bang. That sounds like a long time, but the time required for random fluctuations to make anything interesting is enormously larger than that. (To make something highly ordered out of something with entropy S, you have to wait for a time of order eS. Since macroscopic objects have more than 1023 particles, S is at least that large. So we’re talking very long times indeed, so long that it doesn’t matter whether you’re measuring in microseconds or billions of years.) Besides, the universe is not a box of gas; it’s expanding and emptying out, right?
Ah, but things are a bit more complicated than that. We now know that the universe is not only expanding, but also accelerating. The simplest explanation for that — not the only one, of course — is that empty space is suffused with a fixed amount of vacuum energy, a.k.a. the cosmological constant. Vacuum energy doesn’t dilute away as the universe expands; there’s nothing in principle from stopping it from lasting forever. So even if the universe is finite in age now, there’s nothing to stop it from lasting indefinitely into the future.
But, you’re thinking, doesn’t the universe get emptier and emptier as it expands, leaving no particles to fluctuate? Only up to a point. A universe with vacuum energy accelerates forever, and as a result we are surrounded by a cosmological horizon — objects that are sufficiently far away can never get to us or even send signals, as the space in between expands too quickly. And, as Stephen Hawking and Gary Gibbons pointed out in the 1970’s, such a cosmology is similar to a black hole: there will be radiation associated with that horizon, with a constant temperature.
In other words, a universe with a cosmological constant is like a box of gas (the size of the horizon) which lasts forever with a fixed temperature. Which means there are random fluctuations. If we wait long enough, some region of the universe will fluctuate into absolutely any configuration of matter compatible with the local laws of physics. Atoms, viruses, people, dragons, what have you. The room you are in right now (or the atmosphere, if you’re outside) will be reconstructed, down to the slightest detail, an infinite number of times in the future. In the overwhelming majority of times that your local environment does get created, the rest of the universe will look like a high-entropy equilibrium state (in this case, empty space with a tiny temperature). All of those copies of you will think they have reliable memories of the past and an accurate picture of what the external world looks like — but they would be wrong. And you could be one of them.
That would be bad.
Discussions of the Boltzmann Brain problem typically occur in the context of speculative ideas like eternal inflation and the multiverse. (Not that there’s anything wrong with that.) And, let’s admit it, the very idea of orderly configurations of matter spontaneously fluctuating out of chaos sounds a bit loopy, as critics have noted. But everything I’ve just said is based on physics we think we understand: quantum field theory, general relativity, and the cosmological constant. This is the real world, baby. Of course it’s possible that we are making some subtle mistake about how quantum field theory works, but that is more speculative than taking the straightforward prediction seriously.
Modern cosmologists have a favorite default theory of the universe, labeled ΛCDM, where “Λ” stands for the cosmological constant and “CDM” for Cold Dark Matter. What we’re pointing out is that ΛCDM, the current leading candidate for an accurate description of the cosmos, can’t be right all by itself. It has a Boltzmann Brain problem, and is therefore cognitively unstable, and unacceptable as a physical theory.
Can we escape this unsettling conclusion? Sure, by tweaking the physics a little bit. The simplest route is to make the vacuum energy not really a constant, e.g. by imagining that it is a dynamical field (quintessence). But that has it’s own problems, associated with very tiny fine-tuned parameters. A more robust scenario would be to invoke quantum vacuum decay. Maybe the vacuum energy is temporarily constant, but there is another vacuum state out there in field space with an even lower energy, to which we can someday make a transition. What would happen is that tiny bubbles of the lower-energy configuration would appear via quantum tunneling; these would rapidly grow at the speed of light. If the energy of the other vacuum state were zero or negative, we wouldn’t have this pesky Boltzmann Brain problem to deal with.
Fine, but it seems to invoke some speculative physics, in the form of new fields and a new quantum vacuum state. Is there any way to save ΛCDM without invoking new physics at all?
The answer is — maybe! This is where Kim and I come in, although some of the individual pieces of our puzzle were previously put together by other authors. The first piece is a fun bit of physics that hit the news media earlier this year: the possibility that the Higgs field can itself support another vacuum state other than the one we live in. (The reason why this is true is a bit subtle, but it comes down to renormalization group effects.) That’s right: without introducing any new physics at all, it’s possible that the Higgs field will decay via bubble nucleation some time in the future, dramatically changing the physics of our universe. The whole reason the Higgs is interesting is that it has a nonzero value even in empty space; what we’re saying here is that there might be an even larger value with an even lower energy. We’re not there now, but we could get there via a phase transition. And that, Kim and I point out, has a possibility of saving us from the Boltzmann Brain problem.
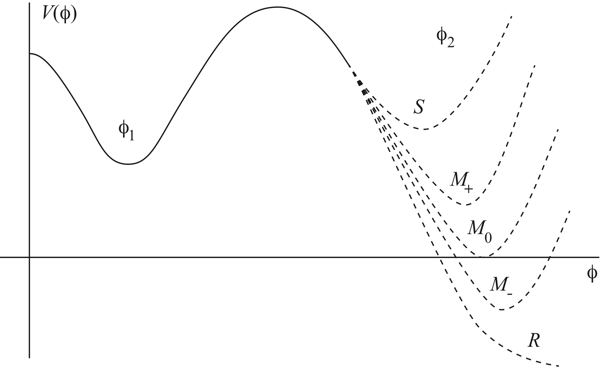
Imagine that the plot of “energy of empty space” versus “value of the Higgs field” looks like this.
φ is the value of the Higgs field. Our current location is φ1, where there is some positive energy. Somewhere out at a much larger value φ2, with a different energy. If the energy at φ2 is greater than at φ1, our current vacuum is stable. If it’s any lower value, we are “metastable”; our current situation can last for a while, but eventually we will transition to a different state. Or the Higgs can have no other vacuum far away, a “runaway” solution. (Note that if the energy in the other state is negative, space inside the bubbles of new vacuum will actually collapse to a Big Crunch rather than expanding.)
But even if that’s true, it’s not good enough by itself. Imagine that there is another vacuum state, and that we can nucleate bubbles that create regions of that new phase. The bubbles will expand at nearly the speed of light — but will they ever bump into other bubbles, and complete the transition from our current phase to the new one? Will the transition “percolate,” in other words? The answer is only “yes” if the bubbles are created rapidly enough. If they are created too slowly, the cosmological horizons come into play — spacetime expands so fast that two random bubbles will never meet each other, and the volume of space left in the original phase (the one we’re in now) keeps growing without bound. (This is the “graceful exit problem” of Alan Guth’s original inflationary-universe scenario.)
So given that the Higgs field might support a different quantum vacuum, we have two questions. First, is our current vacuum stable, or is there actually a lower-energy vacuum to which we can transition? Second, if there is a lower-energy vacuum, does our vacuum decay fast enough that the transition percolates, or do we get stuck with an ever-increasing amount of space in the current phase?
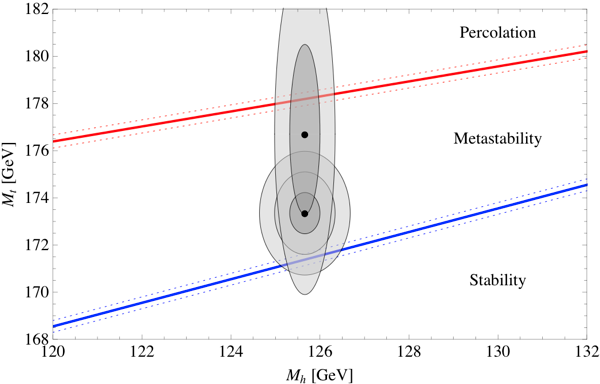
The answers depend on the precise value of the parameters that specify the Standard Model of particle physics, and therefore determine the renormalized Higgs potential. In particular, two parameters turn out to be the most important: the mass of the Higgs itself, and the mass of the top quark. We’ve measured both, but of course our measurements only have a certain precision. Happily, the answers to the two questions we are asking (is our vacuum stable, and does it decay quickly enough to percolate) have already been calculated by other groups: the stability question has been tackled (most recently, after much earlier work) by Buttazzo et al., and the percolation question has been tackled by Arkani-Hamed et al. Here are the answers, plotted in the parameter space defined by the Higgs mass and the top mass. (Dotted lines represent uncertainties in another parameter, the QCD coupling constant.)
We are interested in the two diagonal lines. If you are below the bottom line, the Higgs field is stable, and you definitely have a Boltzmann Brain problem. If you are in between the two lines, bubbles nucleate and grow, but they don’t percolate, and our current state survives. (Whether or not there is a Boltzmann-Brain problem is then measure-dependent, see below.) If you are above the top line, bubbles nucleate quite quickly, and the transition percolates just fine. However, in that region the bubbles actually nucleate too fast; the phase transition should have already happened! The favored part of this diagram is actually the top diagonal line itself; that’s the only region in which we can definitely avoid Boltzmann Brains, but can still be here to have this conversation.
We’ve also plotted two sets of ellipses, corresponding to the measured values of the Higgs and top masses. The most recent LHC numbers put the Higgs mass at 125.66 ± 0.34 GeV, which is quite good precision. The most recent consensus number for the top quark mass is 173.20 ± 0.87 GeV. Combining these results gives the lower of our two sets of ellipses, where we have plotted one-sigma, two-sigma, and three-sigma contours. We see that the central value is in the “metastable” regime, where there can be bubble nucleation but the phase transition is not fast enough to percolate. The error bars do extend into the stable region, however.
Interestingly, there has been a bit of controversy over whether this measured value of the top quark mass is the same as the parameter we use in calculating the potential energy of the Higgs field (the so-called “pole” mass). This is a discussion that is a bit outside my expertise, but a very recent paper by the CMS collaboration tries to measure the number we actually want, and comes up with much looser error bars: 176.7 ± 3.6 GeV. That’s where we got our other set of ellipses (one-sigma and two-sigma) from. If we take these numbers at face value, it’s possible that the top quark could be up there at 178 GeV, which would be enough to live on the viability line, where the phase transition will happen quickly but not too quickly. My bet would be that the consensus numbers are close to correct, but let’s put it this way: we are predicting that either the pole mass of the top quark turns out to be 178 GeV, or there is some new physics that kicks in to destabilize our current vacuum.
I was a bit unclear about what happens in the vast “metastable” region between stability and percolation. That’s because the situation is actually a bit unclear. Naively, in that region the volume of space in our current vacuum grows without bound, and Boltzmann Brains will definitely dominate. But a similar situation arises in eternal inflation, leading to what’s called the cosmological measure problem. The meat of our paper was not actually plotting a couple of curves that other people had calculated, but attempting to apply approaches to the eternal-inflation measure problem to our real-world situation. The results were a bit inconclusive. In most measures, it’s safe to say, the Boltzmann Brain problem is as bad as you might have feared. But there is at least one — a modified causal-patch measure with terminal vacua, if you must know — in which the problem is avoided. I’m not sure if there is some principled reason to believe in this measure other than “it gives an acceptable answer,” but our results suggest that understanding cosmological measure theory may be important even if you don’t believe in eternal inflation.
A final provocative observation that I’ve been saving for last. The safest place to be is on the top diagonal line in our diagram, where we have bubbles nucleating fast enough to percolate but not so fast that they should have already happened. So what does it mean, “fast enough to percolate,” anyway? Well, roughly, it means you should be making new bubbles approximately once per current lifetime of our universe. (Don Page has done a slightly more precise estimate of 20 billion years.) On the one hand, that’s quite a few billion years; it’s not like we should rush out and buy life insurance. On the other hand, it’s not that long. It means that roughly half of the lifetime of our current universe has already happened. And the transition could happen much faster — it could be tomorrow or next year, although the chances are quite tiny.
For our purposes, avoiding Boltzmann Brains, we want the transition to happen quickly. Amusingly, most of the existing particle-physics literature on decay of the Higgs field seems to take the attitude that we should want it to be completely stable — otherwise the decay of the Higgs will destroy the universe! It’s true, but we’re pointing out that this is a feature, not a bug, as we need to destroy the universe (or at least the state its currently in) to save ourselves from the invasion of the Boltzmann Brains.
All of this, of course, assumes there is no new physics at higher energies that would alter our calculations, which seems an unlikely assumption. So the alternatives are: new physics, an improved understanding of the cosmological measure problem, or a prediction that the top quark is really 178 GeV. A no-lose scenario, really.
What about the converse? Is it conceivable that one could prove that one is a BB?
It seems that a few folks who are (otherwise) well respected believe that it is likely that we are living in a simulation. Have they not understood your argument, or my argument above?
If you were a BB, chances are you would look around and see the rest of the universe in thermal equilibrium, so that would be a clue. Sadly, you wouldn’t know it was a clue, since all of your ideas about how the universe works will have randomly fluctuated into your brain, so you would have no reason to trust them.
I think it’s much harder to live in a simulation than some other people believe. But it’s certainly possible that you could live in a simulation that obeyed rules you could self-consistently figure out. Or you could live in one where stuff just randomly happened, or happened just to fool you.
The point is: we have to act as if the world makes sense, which includes constructing sense-making models of the world.
And real brains in real universes are more than random fluctuations?
I thought the universe came from a random fluctuation and so would not be different from a BB. But we cannot see outside it so internally it looks self-consistent.
I think we agree that it’s necessary to make the assumption that we’re not Boltzmann brains. But then why is it a problem if there are also (in addition to us ordinary observers) a whole lot of Boltzmann brains somewhere in spacetime? We already know that we humans are vastly outnumbered by (for example) insects here on Earth; why would it matter if we were also vastly outnumbered by BBs throughout the cosmos? Why does physics have to arrange itself so that this is not the case?
Mark, it’s no problem at all that there are lots of BB’s elsewhere in the universe. As we said in the paper (and blog post), the problem is that there are many observers with exactly our macroscopic data, but for whom all of their impressions of the outside world are likely to be false. Those folks can’t “look around and see that they aren’t a Boltzmann Brain,” any more than we can, because they see exactly what we see.
You might say “so wait five minutes and they will see something different.” That’s very probable, yes. But those who see the same things that we will see will still overwhelm the number of ordinary observers who see that. I claim there is no consistent and motivated way to only pick out “good” observers when most of them are random fluctuations out of equilibrium.
Sean, the assumption that we’re not BBs seems fully “consistent and motivated” to me. And once I’ve made this assumption, I simply don’t care how many BBs (with precisely my current data) there may or may not be throughout spacetime, as long as my assumption that I’m not a BB continues to hold up. After all, in a universe in which ordinary observers (OOs) are vastly outnumbered by BBSs, nevertheless somebody still has to be the OOs! Why not us?
This is a point of philosophy, not physics. Given the assumption that we’re OOs, you want to insist that the universe arrange itself to have no (or very few) BBs, whereas I’m happy to let the universe do whatever it wants.
Mark, if your cosmological model says there are 10^50 (or whatever) observers with precisely your current data, and all but one of them will soon observe a particular physical phenomenon (something that would reveal that their past had higher entropy rather than lower), what possible reason would you have for predicting ahead of time that you are the one, given that you admit they are all in identical local situations, with no way of distinguishing themselves from each other?
Hint: it’s because you don’t really believe there are all those other observers. We’re just trying to construct models in which that’s true.
Why would I care if I am a BB, OO, or living in a simulation? I would argue they would be indistinguishable.
“…there is nothing more real than dream. This statement only makes sense once it is understood that normal waking life is as unreal as dream, and in exactly the same way.” – Tenzin Wangyal Rinpoche in The Tibetan Yogas of Dream and Sleep
“… do not alter the reality of the dream; do not divorce the magic of the story or the vitality of the myth. Do not forget that rivers can exist without water but not without shores. Believe me reality means nothing unless we can verify it in dreams.”- Don Manuel Cordova (Ino Moxo) speaking in Cesar Calvo’s The Three Halves of Ino Moxo.
Sean, my reason for “predicting ahead of time” that I am the one ordinary observer in a universe filled with Boltzmann brains is precisely the reason that you have given (and which I originally learned from you, and for which you are credited in my paper with Jim Hartle): it is “cognitively unstable” to make any other prediction.
As best I can tell, you want to say both that it’s “cognitively unstable” to assume that we’re BBs, and that we must be “equally likely” to be any observer (OO or BB) with our data. Then, to avoid having these two assumptions contradict each other, you require the universe not have any BBs in it.
But another option is to drop one of your two contradictory assumptions. The one I would like to drop is the assumption that we’re “equally likely” to be any observer with our data. As Jim Hartle and I explain, the “equally likely” assumption cannot be derived as a consequence of any physical theory. Therefore, insisting upon it is a philosophical stance, not a scientific one.
But cognitive stability isn’t nearly strong enough to rule out all kinds of fluctuations. If you give equal credence to all observers with precisely equal data (which I think is the right thing to do, for reasons not fully articulated here), cognitive instability helps you rule out a model in which most such observers have an immediate higher-entropy past. But within such a model, if you try to say “but I’m one of the cognitively stable ones,” that’s still a much weaker criterion than “I’m an ordinary observer who came from a Big Bang.” Given not only your present data, but also a demand that all of the orderliness you observe evolved from lower-entropy past configurations, you would still predict with overwhelming likelihood that your future observations will reveal dramatic thermodynamic irregularities. But you don’t want to make that prediction, even though it’s right there for you to seize and await your imminent Nobel Prize! Because deep in your heart you don’t actually believe in all those observers that your theory predicts, or for some reason you don’t take them seriously.
I found your Boltzmann’s brain paper very interesting and fully in line with Boltzmann’s estimate of the Poincare recurrence time, and I could not understand why Dr. Distler in his “Musing” is telling us that he normally would not touch such a paper with a ten foot pole. I cannot touch a paper by Dr. Distler with a pole of any length because in the last twenty years he has by his own account out of 38 papers only one paper published by himself without a co-author.
Sean, well now I’m unsure of your precise definition of “cognative instability”, so I’m happy to just flatly make the assumption that “I’m an ordinary observer who came from a Big Bang.”
You say that you want to “give equal credence to all observers with precisely equal data” which you say “is the right thing to do, for reasons not fully articulated here”. My main point is that this is an assumption, one that cannot be derived from any physical theory.
I am therefore skeptical of your program of restricting physical theory by means of such an assumption. I worry about the spectacular failure of assumptions that seem (to me) to be closely analogous, such as assuming that humans would turn out to be typical animals on Earth. I do not believe that typicality assumptions should be used to restrict the realm of physical possibilities in the absence of an active selection process that scanned across those possibilities (which is what happens in ordinary laboratory experiments).
Boltzmann called.
He’s like his brain back.
Mark, I have a lot of sympathy with you about overly general typicality assumptions, but for people in absolutely indistinguishable situations I think it’s perfectly correct to assume a uniform distribution. For some formal arguments, see Elga (http://philsci-archive.pitt.edu/1036/1/drevil.pdf) or Neal (http://arxiv.org/abs/math/0608592).
Of course one always has to make some assumptions (I am not being tricked by an evil demon, etc), but it’s sensible to minimize what those assumptions are. I am saying that indistinguishable events should be given equal likelihoods, which seems to me the closest we can come to “taking what the theory itself says.” On the other hand, the assumption “I am an ordinary observer” has absolutely no justification at all, if you believe there are many non-ordinary observers in identical epistemic circumstances. Indeed, the assumption “I am not an ordinary observer” would, in such a scenario, turn out to be useful and correct in the overwhelming majority of such circumstances.
I really think that people don’t take the implications of this kind of cosmological scenario seriously. They “know” that they are an ordinary observer living 14 billion years after a low-entropy Big Bang, so the existence of jillions of identical observers in the future doesn’t bother them. They don’t quite internalize that they are accepting the existence of jillions of observers who feel exactly the same way, all of whom are absolutely convinced that they are “ordinary,” and all of whom are wrong. Because they “know” that they are not one of them.
Why not just admit that we should seek cosmological models in which people who feel that they are ordinary observers are probably right?
Sean, I’m familiar with Neal’s paper; Jim & I cite it in our first paper on typicality, http://arxiv.org/abs/0704.2630. But I’m surprised to see you mention it, since Neal agrees with me! Most of his paper treats only the use of typicality arguments in a universe small enough to make an exact copy of us highly unlikely. Only at the end, in section 7.2, does he briefly discuss what to do if there are multiple exact copies. He says, “As an interim solution, I advocate simply ignoring the problem of infinity, which is certainly what everyone does in everyday life.” (By “infinity”, he means a universe large enough to make multiple exact copies likely.) In other words, assume we’re not Boltzmann brains, even if there are a lot of them out there! At no point does Neal endorse (or even discuss) your “equally likely” assumption.
I had not previously seen Elga’s paper. He does argue explicitly for “equally likely”, but I find his arguments unconvincing. In particular, no way should Dr. Evil surrender!!! (Elga disagrees, and I presume you do as well.) But at the end, Elga says “I am not entirely comfortable with that conclusion”, and then gives a reducto ad absurdum argument against “equally likely”. I find this argument much more convincing that his earlier arguments in favor!
FWIW, I believe that I have fully “internalized” that I am “accepting the existence of jillions of observers who feel exactly the same way, all of whom are absolutely convinced that they are “ordinary,” and all of whom are wrong.” I don’t “know” that I’m not a Boltzmann brain, but I assume it, because to assume otherwise is (as I learned from you!) “cognitively unstable”.
Incidentally, I’m actually defending you over on Jacques Distler’s blog … 🙂
Hmm, I’ll have to look back at Neal’s paper, it’s been a while. His main goal is to say we should condition over all the data we have, rather than thinking of ourselves as typical in some larger reference class — with which I agree, and for which I credit you and Jim, as far as my own understanding is concerned. But I thought he agreed with me that within the set of people with exactly the same data, we should distribute credence uniformly, so I’ll have to re-check that.
Thanks for defending me at Jacques’s place — good luck with that. 🙂
Pingback: ¿Puede el bosón de Higgs salvarnos de la amenaza de los cerebros de Boltzmann?
Say, Prof. Carroll, somebody over on the “Not Even Wrong” blog sure doesn’t like your entry on Boltzmann brains. (And he can’t even spell!) Check the quote below:
“A sign of the times is to see a talented fellow like Sean Carrol writing some crazy article about ‘Botltzmann brains’. ”
(At least he thinks you’re talented, tho …)
Entropy appears to be the one thing that is never questioned, the constant in these scenarios. Why not introduce a bit more chaos by suggesting that in some parts of the multiverse, entropy is reversed? What we consider to be a high entropy state would then behave like something we would consider to be, in this region, a low entropy state, and vice-versa?
I think there could be more sense out of all this madness. I don’t think the Higgs Field can be determined by complete chaos. Say if you where to assume for a moment that time symmetry cannot be broken but only prevented. Like the Grandfather Paradox, instead of not being able to travel back in time to kill your own grandfather, you would just be prevented from killing your own grandfather. This could happen in a number of different ways.
But how do you determine what way the universe will achieve this goal of not allowing someone to alter their own eigenstate? It is beyond the realm of known science. I think it could be determined by a couple of things. It could use a method that would then require the least amount of energy, or it could mimic recent events that happened that prevented a similar situation. I think science needs to reach a consensus on the correct solution to the Grandfather Paradox. If I was going to make up the laws of physics that govern it I would say;
The first law would be that you cannot alter your own eigenstate by breaking local temporal symmetry.
The second law would be that if you altered the eigenstate of your own past locally then it would only create another separate eigenstate.
The third law would be that the universe would then use a combination of similar events that prevented you from altering your own eigenstate that would use the least amount of energy.
The forth law would be that you can alter your own eigenstate if it is not breaking local symmetry but it is separated by long distances in spacetime, an eigenstate could fluctuate between different states if given enough time and doesn’t have to correspond to being at the same state in two different periods of time that it originally was in that lead to each state.
They need to be sure to test this out when they get around to being able to create a real time machine!
I’d also like to suggest that a boltzmann brain with a disordered and incoherent set of memories is much more likely than one with ordered memories. Somewhat less likely would be semi-ordered memories. But there would be blanks and inconsistencies and apparent contradictions. The most likely sort of boltzmann brain would be severely impaired and perhaps “insane”.
@ Rick
I think your suggestion would be obvious given the information provided in the blog here. I don’t think our brains can be Boltzmann Brains, because if they where we would always be aware of this occurrence of people always randomly going insane all the time. It would be far less likely to observe Boltzmann Brains that never go insane. That would mean that there would be a very low probability that the Boltzmann Brain Theory is even true. We would have to be living in a scenario where the most unlikely Boltzmann Brain that governs human consciousness is the scenario that governs most of our brains.
It would be like accepting Planet of the Apes as a possible alternate universe, and we just happened to advance in technology instead of the apes just by chance when both situations would have been just as likely as the other. The problem with the theory is that Planet of the Apes shouldn’t be put on equal footing as humans. If you had a large sample of alternate universes only the humans will advance and not the apes.
Well, I look at my own memories and thought processes and find that there is much to be desired in terms of continuity, coherence, and consistency. And then I look at my fellow beings and evaluate their actions and words and then I must conclude that if I AM in fact a Boltzmann brain I must be one of the rather more likely manifestations. My tongue is a bit in my cheek here. But, then, with my tongue in my cheek I frequently bite it. Is that not more proof that if I am a Boltzmann brain I am not one of the very few superbly functioning examples. OW!
I think a particular assumption is implicitly being made here that random fluctuations in a vacuum or nothing just exist without being affected by something that collapses their wave function of possibility into actual fluctuations that don’t sum to zero and thus not exist. If humans are not Bolzmann brains, then their observations can cause the collapsing of the wave function of nothing to enable sufficient order for humans and this universe to exist. With causality working in both directions in time according to quantum mechanics, human observations/will power, etc. can cause such collapses that led to the universe with humans in it.
Human beings being boltzmann brains thus isn’t really possible unless one makes the unjustifiable assumption that “in the beginning” there were random fluctuations. Where did they come from? If from nothing, why aren’t they just waves of possibility that smooths to nothing unless something collapses those waves? Human beings, and/or some other conscious beings internal to the universe, including future people, seem to be the most likely answer.
In contrast, one problem with an external creator for the universe and humans (like a god in most religions, or a computer programer where the universe and humans are just computer simulations) is where do those external creators come from? Random fluctuations in Nothing? But who created those random fluctuations that don’t act like a wave summing to nothing? Once again, conscious beings internal to the universe (that created everything because they were possible) is really the only answer I see.
See for example Kuenftigen Leuten’s THE MEANING OF LIFE, THE UNIVERSE, AND NOTHING (published in 2011 by European Press Academic Publishing; Florence, Italy). That book also explains where human consciousness came from (i.e., how it evolved and what it actually is), but that’s a somewhat more complex issue.