Guest Post: Tom Banks on Probability and Quantum Mechanics

The lure of blogging is strong. Having guest-posted about problems with eternal inflation, Tom Banks couldn’t resist coming back for more punishment. Here he tackles a venerable problem: the interpretation of quantum mechanics. Tom argues that the measurement problem in QM becomes a lot easier to understand once we appreciate that even classical mechanics allows for non-commuting observables. In that sense, quantum mechanics is “inevitable”; it’s actually classical physics that is somewhat unusual. If we just take QM seriously as a theory that predicts the probability of different measurement outcomes, all is well.

Tom’s last post was “technical” in the sense that it dug deeply into speculative ideas at the cutting edge of research. This one is technical in a different sense: the concepts are presented at a level that second-year undergraduate physics majors should have no trouble following, but there are explicit equations that might make it rough going for anyone without at least that much background. The translation from LaTeX to WordPress is a bit kludgy; here is a more elegant-looking pdf version if you’d prefer to read that.

—————————————-

Rabbi Eliezer ben Yaakov of Nahariya said in the 6th century, “He who has not said three things to his students, has not conveyed the true essence of quantum mechanics. And these are Probability, Intrinsic Probability, and Peculiar Probability”.

Probability first entered the teachings of men through the work of that dissolute gambler Pascal, who was willing to make a bet on his salvation. It was a way of quantifying our risk of uncertainty. Implicit in Pascal’s thinking, and all who came after him was the idea that there was a certainty, even a predictability, but that we fallible humans may not always have enough data to make the correct predictions. This implicit assumption is completely unnecessary and the mathematical theory of probability makes use of it only through one crucial assumption, which turns out to be wrong in principle but right in practice for many actual events in the real world.

For simplicity, assume that there are only a finite number of things that one can measure, in order to avoid too much math. List the possible measurements as a sequence

The a_N are the quantities being measured and each could have a finite number of values. Then a probability distribution assigns a number P(A) between zero and one to each possible outcome. The sum of the numbers has to add up to one. The so called frequentist interpretation of these numbers is that if we did the same measurement a large number of times, then the fraction of times or frequency with which we’d find a particular result would approach the probability of that result in the limit of an infinite number of trials. It is mathematically rigorous, but only a fantasy in the real world, where we have no idea whether we have an infinite amount of time to do the experiments. The other interpretation, often called Bayesian, is that probability gives a best guess at what the answer will be in any given trial. It tells you how to bet. This is how the concept is used by most working scientists. You do a few experiments and see how the finite distribution of results compares to the probabilities, and then assign a confidence level to the conclusion that a particular theory of the data is correct. Even in flipping a completely fair coin, it’s possible to get a million heads in a row. If that happens, you’re pretty sure the coin is weighted but you can’t know for sure.

Physical theories are often couched in the form of equations for the time evolution of the probability distribution, even in classical physics. One introduces “random forces” into Newton’s equations to “approximate the effect of the deterministic motion of parts of the system we don’t observe”. The classic example is the Brownian motion of particles we see under the microscopic, where we think of the random forces in the equations as coming from collisions with the atoms in the fluid in which the particles are suspended. However, there’s no a priori reason why these equations couldn’t be the fundamental laws of nature. Determinism is a philosophical stance, an hypothesis about the way the world works, which has to be subjected to experiment just like anything else. Anyone who’s listened to a geiger counter will recognize that the microscopic process of decay of radioactive nuclei doesn’t seem very deterministic.

The place where the deterministic hypothesis and the laws of classical logic are put into the theory of probability is through the rule for combining probabilities of independent alternatives. A classic example is shooting particles through a pair of slits. One says, “the particle had to go through slit A or slit B and the probabilities are independent of each other, so,

It seems so obvious, but it’s wrong, as we’ll see below. The probability sum rule, as the previous equation is called, allows us to define conditional probabilities. This is best understood through the example of hurricane Katrina. The equations used by weather forecasters are probabilistic in nature. Long before Katrina made landfall, they predicted a probability that it would hit either New Orleans or Galveston. These are, more or less, mutually exclusive alternatives. Because these weather probabilities, at least approximately, obey the sum rule, we can conclude that the prediction for what happens after we make the observation of people suffering in the Superdome, doesn’t depend on the fact that Katrina could have hit Galveston. That is, that observation allows us to set the probability that it could have hit Galveston to zero, and re-scale all other probabilities by a common factor so that the probability of hitting New Orleans was one.

Note that if we think of the probability function P(x,t) for the hurricane to hit a point x and time t to be a physical field, then this procedure seems non-local or a-causal. The field changes instantaneously to zero at Galveston as soon as we make a measurement in New Orleans. Furthermore, our procedure “violates the weather equations”. Weather evolution seems to have two kinds of dynamics. The deterministic, local, evolution of P(x,t) given by the equation, and the causality violating projection of the probability of Galveston to zero and rescaling of the probability of New Orleans to one, which is mysteriously caused by the measurement process. Recognizing P to be a probability, rather than a physical field, shows that these objections are silly.

Nothing in this discussion depends on whether we assume the weather equations are the fundamental laws of physics of an intrinsically uncertain world, or come from neglecting certain unmeasured degrees of freedom in a completely deterministic system.

The essence of QM is that it forces us to take an intrinsically probabilistic view of the world, and that it does so by discovering an unavoidable probability theory underlying the mathematics of classical logic. In order to describe this in the simplest possible way, I want to follow Feynman and ask you to think about a single ammonia molecule, NH₃. A classical picture of this molecule is a pyramid with the nitrogen at the apex and the three hydrogens forming an equilateral triangle at the base. Let’s imagine a situation in which the only relevant measurement we could make was whether the pyramid was pointing up or down along the z axis. We can ask one question Q, “Is the pyramid pointing up?” and the molecule has two states in which the answer is either yes or no. Following Boole, we can assign these two states the numerical values 1 and 0 for Q, and then the “contrary question” 1 − Q has the opposite truth values. Boole showed that all of the rules of classical logic could be encoded in an algebra of independent questions, satisfying

where the Kronecker symbol δ_ij = 1 if i = j and 0 otherwise. i,j run from 1 to N, the number of independent questions. We also have ∑Q_i = 1, meaning that one and only one of the questions has the answer yes in any state of the system. Our ammonia molecule has only two independent questions, Q and 1 − Q. Let me also define s_z = 2Q − 1 = ±1, in the two different states. Computer aficionadas will recognize our two question system as a bit.

We can relate this discussion of logic to our discussion of probability of measurements by introducing observables A = ∑a_i Q_i , where the a_i are real numbers, specifying the value of some measurable quantity in the state where only Q_i has the answer yes. A probability distribution is then just a special case ρ = ∑p_i Q_i, where p_i is non-negative for each i and ∑p_i = 1.

Restricting attention to our ammonia molecule, we denote the two states as | ±_z 〉 and summarize the algebra of questions by the equation

We say that ” the operator s_z acting on the states | ±_z 〉 just multiplies them by (the appropriate ) number”. Similarly, if A = a₊ Q + a₋ (1 − Q) then

The expected value of the observable Aⁿ in the probability distribution ρ is

In the last equation we have used the fact that all of our “operators” can be thought of as two by two matrices acting on a two dimensional space of vectors whose basis elements are |±_z 〉. The matrices can be multiplied by the usual rules and the trace of a matrix is just the sum of its diagonal elements. Our matrices are

They’re all diagonal, so it’s easy to multiply them.

So far all we’ve done is rewrite the simple logic of a single bit as a complicated set of matrix equations, but consider the operation of flipping the orientation of the molecule, which for nefarious purposes we’ll call s_x,

This has matrix

Note that s_z² = s_x² = 1, and s_x s_z = − s_z s_x = − i s_y , where the last equality is just a definition. This definition implies that s_y s_a = − s_a s_y, for a = x or a = z, and it follows that s_y² = 1. You can verify these equations by using matrix multiplication, or by thinking about how the various operations operate on the states (which I think is easier). Now consider for example the quantity B ≡ b_x s_x + b_z s_z . Then B² = b_x² + b_z² , which suggests that B is a quantity which takes on the possible values ±√{b₊² + b₋²}. We can calculate

for any choice of probability distribution. If n = 2k it’s just

whereas if n = 2k + 1 it’s

This is exactly the same result we would get if we said that there was a probability P₊ (B) for B to take on the value √{b_z² + b_x²} and probability P₋ (B) = 1 − P₊ (B), to take on the opposite value, if we choose

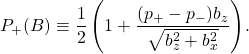
The most remarkable thing about this formula is that even when we know the answer to Q with certainty (p₊ = 1 or 0), B is still uncertain.

We can repeat this exercise with any linear combination b_x s_x + b_y s_y + b_z s_z. We find that in general, if we force one linear combination to be known with certainty, that all linear combinations where the vector (c_x, c_y, c_z) is not parallel to (b_x , b_y, b_z) are uncertain. This is the same as the condition guaranteeing that the two linear combinations commute as matrices.

Pursuing the mathematics of this further would lead us into the realm of eigenvalues of Hermitian matrices, complete ortho-normal bases and other esoterica. But the main point to remember is that any system we can think about in terms of classical logic inevitably contains in it an infinite set of variables in addition to the ones we initially thought about as the maximum set of things we thought could be measured. When our original variables are known with certainty, these other variables are uncertain but the mathematics gives us completely determined formulas for their probability distributions.

Another disturbing fact about the mathematical probability theory for non-compatible observables that we’ve discovered, is that it does NOT satisfy the probability sum rule. This is because, once we start thinking about incompatible observables, the notion of either this or that is not well defined. In fact we’ve seen that when we know “definitely for sure” that s_z is 1, the probability for B to take on its positive value could be any number between zero and one, depending on the ratio of b_z and b_x.

Thus QM contains questions that are neither independent nor dependent and the probability sum rule P(s_z or B ) = P(s_z) + P(B) does not make sense because the word or is undefined for non-commuting operators. As a consequence we cannot apply the conditional probability rule to general QM probability predictions. This appears to cause a problem when we make a measurement that seems to give a definite answer. We’ll explain below that the issue here is the meaning of the word measurement. It means the interaction of the system with macroscopic objects containing many atoms. One can show that conditional probability is a sensible notion, with incredible accuracy, for such objects, and this means that we can interpret QM for such objects as if it were a classical probability theory. The famous “collapse of the wave function” is nothing more than an application of the rules of conditional probability, to macroscopic objects, for which they apply.

The double slit experiment famously discussed in the first chapter of Feynman’s lectures on quantum mechanics, is another example of the failure of the probability sum rule. The question of which slit the particle goes through is one of two alternative histories. In Newton’s equations, a history is determined by an initial position and velocity, but Heisenberg’s famous uncertainty relation is simply the statement that position and velocity are incompatible observables, which don’t commute as matrices, just like s_z and s_x. So the statement that either one history or another happened does not make sense, because the two histories interfere.

Before leaving our little ammonia molecule, I want to tell you about one more remarkable fact, which has no bearing on the rest of the discussion, but shows the remarkable power of quantum mechanics. Way back at the top of this post, you could have asked me, “what if I wanted to orient the ammonia along the x axis or some other direction”. The answer is that the operator n_x s_x + n_y s_y + n_z s_z, where (n_x , n_y, n_z) is a unit vector, has definite values in precisely those states where the molecule is oriented along this unit vector. The whole quantum formalism of a single bit, is invariant under 3 dimensional rotations. And who would have ever thought of that? (Pauli, that’s who).

The fact that QM was implicit in classical physics was realized a few years after the invention of QM, in the 1930s, by Koopman. Koopman formulated ordinary classical mechanics as a special case of quantum mechanics, and in doing so introduced a whole set of new observables, which do not commute with the (commuting) position and momentum of a particle and are uncertain when the particle’s position and momentum are definitely known. The laws of classical mechanics give rise to equations for the probability distributions for all these other observables. So quantum mechanics is inescapable. The only question is whether nature is described by an evolution equation which leaves a certain complete set of observables certain for all time, and what those observables are in terms of things we actually measure. The answer is that ordinary positions and momenta are NOT simultaneously determined with certainty.

Which raises the question of why it took us so long to notice this, and why it’s so hard for us to think about and accept. The answers to these questions also resolve “the problem of quantum measurement theory”. The answer lies essentially in the definition of a macroscopic object. First of all it means something containing a large number N of microscopic constituents. Let me call them atoms, because that’s what’s relevant for most everyday objects. For even a very tiny piece of matter weighing about a thousandth of a gram, the number N  ∼ 10²⁰. There are a few quantum states of the system per atom, let’s say 10 to keep the numbers round. So the system has 10¹⁰²⁰ states. Now consider the motion of the center of mass of the system. The mass of the system is proportional to N, so Heisenberg’s uncertainty relation tells us that the mutual uncertainty of the position and velocity of the system is of order [1/N]. Most textbooks stop at this point and say this is small and so the center of mass behaves in a classical manner to a good approximation.

In fact, this misses the central point, which is that under most conditions, the system has of order 10^N different states, all of which have the same center of mass position and velocity (within the prescribed uncertainty). Furthermore the internal state of the system is changing rapidly on the time scale of the center of mass motion. When we compute the quantum interference terms between two approximately classical states of the center of mass coordinate, we have to take into account that the internal time evolution for those two states is likely to be completely different. The chance that it’s the same is roughly 10^−N, the chance that two states picked at random from the huge collection, will be the same. It’s fairly simple to show that the quantum interference terms, which violate the classical probability sum rule for the probabilities of different classical trajectories, are of order 10^−N. This means that even if we could see the [1/N] effects of uncertainty in the classical trajectory, we could model them by ordinary classical statistical mechanics, up to corrections of order 10^−N.

It’s pretty hard to comprehend how small a number this is. As a decimal, it’s a decimal point followed by 100 billion billion zeros and then a one. The current age of the universe is less than a billion billion seconds. So if you wrote one zero every hundredth of a second you couldn’t write this number in the entire age of the universe. More relevant is the fact that in order to observe the quantum interference effects on the center of mass motion, we would have to do an experiment over a time period of order 10^N. I haven’t written the units of time. The smallest unit of time is defined by Newton’s constant, Planck’s constant and the speed of light. It’s 10^{− 44} seconds. The age of the universe is about 10⁶¹ of these Planck units. The difference between measuring the time in Planck times or ages of the universe is a shift from N = 10²⁰ to N = 10²⁰ − 60, and is completely in the noise of these estimates. Moreover, the quantum interference experiment we’re proposing would have to keep the system completely isolated from the rest of the universe for these incredible lengths of time. Any coupling to the outside effectively increases the size of N by huge amounts.

Thus, for all purposes, even those of principle, we can treat quantum probabilities for even mildly macroscopic variables, as if they were classical, and apply the rules of conditional probability. This is all we are doing when we “collapse the wave function” in a way that seems (to the untutored) to violate causality and the Schrodinger equation. The general line of reasoning outlined above is called the theory of decoherence. All physicists find it acceptable as an explanation of the reason for the practical success of classical mechanics for macroscopic objects. Some physicists find it inadequate as an explanation of the philosophical “paradoxes” of QM. I believe this is mostly due to their desire to avoid the notion of intrinsic probability, and attribute physical reality to the Schrodinger wave function. Curiously many of these people think that they are following in the footsteps of Einstein’s objections to QM. I am not a historian of science but my cursory reading of the evidence suggests that Einstein understood completely that there were no paradoxes in QM if the wave function was thought of merely as a device for computing probability. He objected to the contention of some in the Copehagen crowd that the wave function was real and satisfied a deterministic equation and tried to show that that interpretation violated the principles of causality. It does, but the statistical treatment is the right one. Einstein was wrong only in insisting that God doesn’t play dice.

Once we have understood these general arguments, both quantum measurement theory and our intuitive unease with QM are clarified. A measurement in QM is, as first proposed by von Neumann, simply the correlation of some microscopic observable, like the orientation of an ammonia molecule, with a macro-observable like a pointer on a dial. This can easily be achieved by normal unitary evolution. Once this correlation is made, quantum interference effects in further observation of the dial are exponentially suppressed, we can use the conditional probability rule, and all the mystery is removed.

It’s even easier to understand why humans don’t “get” QM. Our brains evolved according to selection pressures that involved only macroscopic objects like fruit, tigers and trees. We didn’t have to develop neural circuitry that had an intuitive feel for quantum interference phenomena, because there was no evolutionary advantage to doing so. Freeman Dyson once said that the book of the world might be written in Jabberwocky, a language that human beings were incapable of understanding. QM is not as bad as that. We CAN understand the language if we’re willing to do the math, and if we’re willing to put aside our intuitions about how the world must be, in the same way that we understand that our intuitions about how velocities add are only an approximation to the correct rules given by the Lorentz group. QM is worse, I think, because it says that logic, which our minds grasp as the basic, correct formulation of rules of thought, is wrong. This is why I’ve emphasized that once you formulate logic mathematically, QM is an obvious and inevitable consequence. Systems that obey the rules of ordinary logic are special QM systems where a particular choice among the infinite number of complementary QM observables remains sharp for all times, and we insist that those are the only variables we can measure. Viewed in this way, classical physics looks like a sleazy way of dodging the general rules. It achieves a more profound status only because it also emerges as an exponentially good approximation to the behavior of systems with a large number of constituents.

To summarize: All of the so-called non-locality and philosophical mystery of QM is really shared with any probabilistic system of equations and collapse of the wave function is nothing more than application of the conventional rule of conditional probabilities. It is a mistake to think of the wave function as a physical field, like the electromagnetic field. The peculiarity of QM lies in the fact that QM probabilities are intrinsic and not attributable to insufficiently precise measurement, and the fact that they do not obey the law of conditional probabilities. That law is based on the classical logical postulate of the law of the excluded middle. If something is definitely true, then all other independent questions are definitely false. We’ve seen that the mathematical framework for classical logic shows this principle to be erroneous. Even when we’ve specified the state of a system completely, by answering yes or no to every possible question in a compatible set, there are an infinite number of other questions one can ask of the same system, whose answer is only known probabilistically. The formalism predicts a very definite probability distribution for all of these other questions.

Many colleagues who understand everything I’ve said at least as well as I do, are still uncomfortable with the use of probability in fundamental equations. As far as I can tell, this unease comes from two different sources. The first is that the notion of “expectation” seems to imply an expecter, and most physicists are reluctant to put intelligent life forms into the definition of the basic laws of physics. We think of life as an emergent phenomenon, which can’t exist at the level of the microscopic equations. Certainly, our current picture of the very early universe precludes the existence of any form of organized life at that time, simply from considerations of thermodynamic equilibrium.

The frequentist approach to probability is an attempt to get around this. However, its insistence on infinite limits makes it vulnerable to the question about what one concludes about a coin that’s come up heads a million times. We know that’s a possible outcome even if the coin and the flipper are completely honest. Modern experimental physics deals with this problem every day both for intrinsically QM probabilities and those that arise from ordinary random and systematic fluctuations in the detector. The solution is not to claim that any result of measurement is definitely conclusive, but merely to assign a confidence level to each result. Human beings decide when the confidence level is high enough that we “believe” the result, and we keep an open mind about the possibility of coming to a different conclusion with more work. It may not be completely satisfactory from a philosophical point of view, but it seems to work pretty well.

The other kind of professional dissatisfaction with probability is, I think, rooted in Einstein’s prejudice that God doesn’t play dice. With all due respect, I think this is just a prejudice. In the 18th century, certain theoretical physicists conceived the idea that one could, in principle, measure everything there was to know about the universe at some fixed time, and then predict the future. This was wild hubris. Why should it be true? It’s remarkable that this idea worked as well as it did. When certain phenomena appeared to be random, we attributed that to the failure to make measurements that were complete and precise enough at the initial time. This led to the development of statistical mechanics, which was also wildly successful. Nonetheless, there was no real verification of the Laplacian principle of complete predictability. Indeed, when one enquires into the basic physics behind much of classical statistical mechanics one finds that some of the randomness invoked in that theory has a quantum mechanical origin. It arises after all from the motion of individual atoms. It’s no surprise that the first hints that classical mechanics was wrong came from failures of classical statistical mechanics like the Gibbs paradox of the entropy of mixing, and the black body radiation laws.

It seems to me that the introduction of basic randomness into the equations of physics is philosophically unobjectionable, especially once one has understood the inevitability of QM. And to those who find it objectionable all I can say is “It is what it is”. There isn’t anymore. All one must do is account for the successes of the apparently deterministic formalism of classical mechanics when applied to macroscopic bodies, and the theory of decoherence supplies that account.

Perhaps the most important lesson for physicists in all of this is not to mistake our equations for the world. Our equations are an algorithm for making predictions about the world and it turns out that those predictions can only be statistical. That this is so is demonstrated by the simple observation of a
Geiger counter and by the demonstration by Bell and others that the statistical predictions of QM cannot be reproduced by a more classical statistical theory with hidden variables, unless we allow for grossly non-local interactions. Some investigators into the foundations of QM have concluded that we should expect to find evidence for this non-locality, or that QM has to be modified in some fundamental way. I think the evidence all goes in the other direction: QM is exactly correct and inevitable and “there are more things in heaven and earth than are conceived of in our naive classical philosophy”. Of course, Hamlet was talking about ghosts…