The lure of blogging is strong. Having guest-posted about problems with eternal inflation, Tom Banks couldn’t resist coming back for more punishment. Here he tackles a venerable problem: the interpretation of quantum mechanics. Tom argues that the measurement problem in QM becomes a lot easier to understand once we appreciate that even classical mechanics allows for non-commuting observables. In that sense, quantum mechanics is “inevitable”; it’s actually classical physics that is somewhat unusual. If we just take QM seriously as a theory that predicts the probability of different measurement outcomes, all is well.
Tom’s last post was “technical” in the sense that it dug deeply into speculative ideas at the cutting edge of research. This one is technical in a different sense: the concepts are presented at a level that second-year undergraduate physics majors should have no trouble following, but there are explicit equations that might make it rough going for anyone without at least that much background. The translation from LaTeX to WordPress is a bit kludgy; here is a more elegant-looking pdf version if you’d prefer to read that.
—————————————-
Rabbi Eliezer ben Yaakov of Nahariya said in the 6th century, “He who has not said three things to his students, has not conveyed the true essence of quantum mechanics. And these are Probability, Intrinsic Probability, and Peculiar Probability”.
Probability first entered the teachings of men through the work of that dissolute gambler Pascal, who was willing to make a bet on his salvation. It was a way of quantifying our risk of uncertainty. Implicit in Pascal’s thinking, and all who came after him was the idea that there was a certainty, even a predictability, but that we fallible humans may not always have enough data to make the correct predictions. This implicit assumption is completely unnecessary and the mathematical theory of probability makes use of it only through one crucial assumption, which turns out to be wrong in principle but right in practice for many actual events in the real world.
For simplicity, assume that there are only a finite number of things that one can measure, in order to avoid too much math. List the possible measurements as a sequence
![]()
The aN are the quantities being measured and each could have a finite number of values. Then a probability distribution assigns a number P(A) between zero and one to each possible outcome. The sum of the numbers has to add up to one. The so called frequentist interpretation of these numbers is that if we did the same measurement a large number of times, then the fraction of times or frequency with which we’d find a particular result would approach the probability of that result in the limit of an infinite number of trials. It is mathematically rigorous, but only a fantasy in the real world, where we have no idea whether we have an infinite amount of time to do the experiments. The other interpretation, often called Bayesian, is that probability gives a best guess at what the answer will be in any given trial. It tells you how to bet. This is how the concept is used by most working scientists. You do a few experiments and see how the finite distribution of results compares to the probabilities, and then assign a confidence level to the conclusion that a particular theory of the data is correct. Even in flipping a completely fair coin, it’s possible to get a million heads in a row. If that happens, you’re pretty sure the coin is weighted but you can’t know for sure.
Physical theories are often couched in the form of equations for the time evolution of the probability distribution, even in classical physics. One introduces “random forces” into Newton’s equations to “approximate the effect of the deterministic motion of parts of the system we don’t observe”. The classic example is the Brownian motion of particles we see under the microscopic, where we think of the random forces in the equations as coming from collisions with the atoms in the fluid in which the particles are suspended. However, there’s no a priori reason why these equations couldn’t be the fundamental laws of nature. Determinism is a philosophical stance, an hypothesis about the way the world works, which has to be subjected to experiment just like anything else. Anyone who’s listened to a geiger counter will recognize that the microscopic process of decay of radioactive nuclei doesn’t seem very deterministic.
The place where the deterministic hypothesis and the laws of classical logic are put into the theory of probability is through the rule for combining probabilities of independent alternatives. A classic example is shooting particles through a pair of slits. One says, “the particle had to go through slit A or slit B and the probabilities are independent of each other, so,
![]()
It seems so obvious, but it’s wrong, as we’ll see below. The probability sum rule, as the previous equation is called, allows us to define conditional probabilities. This is best understood through the example of hurricane Katrina. The equations used by weather forecasters are probabilistic in nature. Long before Katrina made landfall, they predicted a probability that it would hit either New Orleans or Galveston. These are, more or less, mutually exclusive alternatives. Because these weather probabilities, at least approximately, obey the sum rule, we can conclude that the prediction for what happens after we make the observation of people suffering in the Superdome, doesn’t depend on the fact that Katrina could have hit Galveston. That is, that observation allows us to set the probability that it could have hit Galveston to zero, and re-scale all other probabilities by a common factor so that the probability of hitting New Orleans was one.
Note that if we think of the probability function P(x,t) for the hurricane to hit a point x and time t to be a physical field, then this procedure seems non-local or a-causal. The field changes instantaneously to zero at Galveston as soon as we make a measurement in New Orleans. Furthermore, our procedure “violates the weather equations”. Weather evolution seems to have two kinds of dynamics. The deterministic, local, evolution of P(x,t) given by the equation, and the causality violating projection of the probability of Galveston to zero and rescaling of the probability of New Orleans to one, which is mysteriously caused by the measurement process. Recognizing P to be a probability, rather than a physical field, shows that these objections are silly.
Nothing in this discussion depends on whether we assume the weather equations are the fundamental laws of physics of an intrinsically uncertain world, or come from neglecting certain unmeasured degrees of freedom in a completely deterministic system.
The essence of QM is that it forces us to take an intrinsically probabilistic view of the world, and that it does so by discovering an unavoidable probability theory underlying the mathematics of classical logic. In order to describe this in the simplest possible way, I want to follow Feynman and ask you to think about a single ammonia molecule, NH3. A classical picture of this molecule is a pyramid with the nitrogen at the apex and the three hydrogens forming an equilateral triangle at the base. Let’s imagine a situation in which the only relevant measurement we could make was whether the pyramid was pointing up or down along the z axis. We can ask one question Q, “Is the pyramid pointing up?” and the molecule has two states in which the answer is either yes or no. Following Boole, we can assign these two states the numerical values 1 and 0 for Q, and then the “contrary question” 1 − Q has the opposite truth values. Boole showed that all of the rules of classical logic could be encoded in an algebra of independent questions, satisfying
![]()
where the Kronecker symbol δij = 1 if i = j and 0 otherwise. i,j run from 1 to N, the number of independent questions. We also have ∑Qi = 1, meaning that one and only one of the questions has the answer yes in any state of the system. Our ammonia molecule has only two independent questions, Q and 1 − Q. Let me also define sz = 2Q − 1 = ±1, in the two different states. Computer aficionadas will recognize our two question system as a bit.
We can relate this discussion of logic to our discussion of probability of measurements by introducing observables A = ∑ai Qi , where the ai are real numbers, specifying the value of some measurable quantity in the state where only Qi has the answer yes. A probability distribution is then just a special case ρ = ∑pi Qi, where pi is non-negative for each i and ∑pi = 1.
Restricting attention to our ammonia molecule, we denote the two states as | ±z 〉 and summarize the algebra of questions by the equation
![]()
We say that ” the operator sz acting on the states | ±z 〉 just multiplies them by (the appropriate ) number”. Similarly, if A = a+ Q + a− (1 − Q) then
![]()
The expected value of the observable An in the probability distribution ρ is
![]()
In the last equation we have used the fact that all of our “operators” can be thought of as two by two matrices acting on a two dimensional space of vectors whose basis elements are |±z 〉. The matrices can be multiplied by the usual rules and the trace of a matrix is just the sum of its diagonal elements. Our matrices are
![]()
![]()
![]()
![]()
They’re all diagonal, so it’s easy to multiply them.
So far all we’ve done is rewrite the simple logic of a single bit as a complicated set of matrix equations, but consider the operation of flipping the orientation of the molecule, which for nefarious purposes we’ll call sx,
![]()
This has matrix
![]()
Note that sz2 = sx2 = 1, and sx sz = − sz sx = − i sy , where the last equality is just a definition. This definition implies that sy sa = − sa sy, for a = x or a = z, and it follows that sy2 = 1. You can verify these equations by using matrix multiplication, or by thinking about how the various operations operate on the states (which I think is easier). Now consider for example the quantity B ≡ bx sx + bz sz . Then B2 = bx2 + bz2 , which suggests that B is a quantity which takes on the possible values ±√{b+2 + b−2}. We can calculate
![]()
for any choice of probability distribution. If n = 2k it’s just
![]()
whereas if n = 2k + 1 it’s
![]()
This is exactly the same result we would get if we said that there was a probability P+ (B) for B to take on the value √{bz2 + bx2} and probability P− (B) = 1 − P+ (B), to take on the opposite value, if we choose
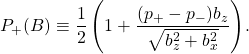
The most remarkable thing about this formula is that even when we know the answer to Q with certainty (p+ = 1 or 0), B is still uncertain.
We can repeat this exercise with any linear combination bx sx + by sy + bz sz. We find that in general, if we force one linear combination to be known with certainty, that all linear combinations where the vector (cx, cy, cz) is not parallel to (bx , by, bz) are uncertain. This is the same as the condition guaranteeing that the two linear combinations commute as matrices.
Pursuing the mathematics of this further would lead us into the realm of eigenvalues of Hermitian matrices, complete ortho-normal bases and other esoterica. But the main point to remember is that any system we can think about in terms of classical logic inevitably contains in it an infinite set of variables in addition to the ones we initially thought about as the maximum set of things we thought could be measured. When our original variables are known with certainty, these other variables are uncertain but the mathematics gives us completely determined formulas for their probability distributions.
Another disturbing fact about the mathematical probability theory for non-compatible observables that we’ve discovered, is that it does NOT satisfy the probability sum rule. This is because, once we start thinking about incompatible observables, the notion of either this or that is not well defined. In fact we’ve seen that when we know “definitely for sure” that sz is 1, the probability for B to take on its positive value could be any number between zero and one, depending on the ratio of bz and bx.
Thus QM contains questions that are neither independent nor dependent and the probability sum rule P(sz or B ) = P(sz) + P(B) does not make sense because the word or is undefined for non-commuting operators. As a consequence we cannot apply the conditional probability rule to general QM probability predictions. This appears to cause a problem when we make a measurement that seems to give a definite answer. We’ll explain below that the issue here is the meaning of the word measurement. It means the interaction of the system with macroscopic objects containing many atoms. One can show that conditional probability is a sensible notion, with incredible accuracy, for such objects, and this means that we can interpret QM for such objects as if it were a classical probability theory. The famous “collapse of the wave function” is nothing more than an application of the rules of conditional probability, to macroscopic objects, for which they apply.
The double slit experiment famously discussed in the first chapter of Feynman’s lectures on quantum mechanics, is another example of the failure of the probability sum rule. The question of which slit the particle goes through is one of two alternative histories. In Newton’s equations, a history is determined by an initial position and velocity, but Heisenberg’s famous uncertainty relation is simply the statement that position and velocity are incompatible observables, which don’t commute as matrices, just like sz and sx. So the statement that either one history or another happened does not make sense, because the two histories interfere.
Before leaving our little ammonia molecule, I want to tell you about one more remarkable fact, which has no bearing on the rest of the discussion, but shows the remarkable power of quantum mechanics. Way back at the top of this post, you could have asked me, “what if I wanted to orient the ammonia along the x axis or some other direction”. The answer is that the operator nx sx + ny sy + nz sz, where (nx , ny, nz) is a unit vector, has definite values in precisely those states where the molecule is oriented along this unit vector. The whole quantum formalism of a single bit, is invariant under 3 dimensional rotations. And who would have ever thought of that? (Pauli, that’s who).
The fact that QM was implicit in classical physics was realized a few years after the invention of QM, in the 1930s, by Koopman. Koopman formulated ordinary classical mechanics as a special case of quantum mechanics, and in doing so introduced a whole set of new observables, which do not commute with the (commuting) position and momentum of a particle and are uncertain when the particle’s position and momentum are definitely known. The laws of classical mechanics give rise to equations for the probability distributions for all these other observables. So quantum mechanics is inescapable. The only question is whether nature is described by an evolution equation which leaves a certain complete set of observables certain for all time, and what those observables are in terms of things we actually measure. The answer is that ordinary positions and momenta are NOT simultaneously determined with certainty.
Which raises the question of why it took us so long to notice this, and why it’s so hard for us to think about and accept. The answers to these questions also resolve “the problem of quantum measurement theory”. The answer lies essentially in the definition of a macroscopic object. First of all it means something containing a large number N of microscopic constituents. Let me call them atoms, because that’s what’s relevant for most everyday objects. For even a very tiny piece of matter weighing about a thousandth of a gram, the number N ∼ 1020. There are a few quantum states of the system per atom, let’s say 10 to keep the numbers round. So the system has 101020 states. Now consider the motion of the center of mass of the system. The mass of the system is proportional to N, so Heisenberg’s uncertainty relation tells us that the mutual uncertainty of the position and velocity of the system is of order [1/N]. Most textbooks stop at this point and say this is small and so the center of mass behaves in a classical manner to a good approximation.
In fact, this misses the central point, which is that under most conditions, the system has of order 10N different states, all of which have the same center of mass position and velocity (within the prescribed uncertainty). Furthermore the internal state of the system is changing rapidly on the time scale of the center of mass motion. When we compute the quantum interference terms between two approximately classical states of the center of mass coordinate, we have to take into account that the internal time evolution for those two states is likely to be completely different. The chance that it’s the same is roughly 10−N, the chance that two states picked at random from the huge collection, will be the same. It’s fairly simple to show that the quantum interference terms, which violate the classical probability sum rule for the probabilities of different classical trajectories, are of order 10−N. This means that even if we could see the [1/N] effects of uncertainty in the classical trajectory, we could model them by ordinary classical statistical mechanics, up to corrections of order 10−N.
It’s pretty hard to comprehend how small a number this is. As a decimal, it’s a decimal point followed by 100 billion billion zeros and then a one. The current age of the universe is less than a billion billion seconds. So if you wrote one zero every hundredth of a second you couldn’t write this number in the entire age of the universe. More relevant is the fact that in order to observe the quantum interference effects on the center of mass motion, we would have to do an experiment over a time period of order 10N. I haven’t written the units of time. The smallest unit of time is defined by Newton’s constant, Planck’s constant and the speed of light. It’s 10− 44 seconds. The age of the universe is about 1061 of these Planck units. The difference between measuring the time in Planck times or ages of the universe is a shift from N = 1020 to N = 1020 − 60, and is completely in the noise of these estimates. Moreover, the quantum interference experiment we’re proposing would have to keep the system completely isolated from the rest of the universe for these incredible lengths of time. Any coupling to the outside effectively increases the size of N by huge amounts.
Thus, for all purposes, even those of principle, we can treat quantum probabilities for even mildly macroscopic variables, as if they were classical, and apply the rules of conditional probability. This is all we are doing when we “collapse the wave function” in a way that seems (to the untutored) to violate causality and the Schrodinger equation. The general line of reasoning outlined above is called the theory of decoherence. All physicists find it acceptable as an explanation of the reason for the practical success of classical mechanics for macroscopic objects. Some physicists find it inadequate as an explanation of the philosophical “paradoxes” of QM. I believe this is mostly due to their desire to avoid the notion of intrinsic probability, and attribute physical reality to the Schrodinger wave function. Curiously many of these people think that they are following in the footsteps of Einstein’s objections to QM. I am not a historian of science but my cursory reading of the evidence suggests that Einstein understood completely that there were no paradoxes in QM if the wave function was thought of merely as a device for computing probability. He objected to the contention of some in the Copehagen crowd that the wave function was real and satisfied a deterministic equation and tried to show that that interpretation violated the principles of causality. It does, but the statistical treatment is the right one. Einstein was wrong only in insisting that God doesn’t play dice.
Once we have understood these general arguments, both quantum measurement theory and our intuitive unease with QM are clarified. A measurement in QM is, as first proposed by von Neumann, simply the correlation of some microscopic observable, like the orientation of an ammonia molecule, with a macro-observable like a pointer on a dial. This can easily be achieved by normal unitary evolution. Once this correlation is made, quantum interference effects in further observation of the dial are exponentially suppressed, we can use the conditional probability rule, and all the mystery is removed.
It’s even easier to understand why humans don’t “get” QM. Our brains evolved according to selection pressures that involved only macroscopic objects like fruit, tigers and trees. We didn’t have to develop neural circuitry that had an intuitive feel for quantum interference phenomena, because there was no evolutionary advantage to doing so. Freeman Dyson once said that the book of the world might be written in Jabberwocky, a language that human beings were incapable of understanding. QM is not as bad as that. We CAN understand the language if we’re willing to do the math, and if we’re willing to put aside our intuitions about how the world must be, in the same way that we understand that our intuitions about how velocities add are only an approximation to the correct rules given by the Lorentz group. QM is worse, I think, because it says that logic, which our minds grasp as the basic, correct formulation of rules of thought, is wrong. This is why I’ve emphasized that once you formulate logic mathematically, QM is an obvious and inevitable consequence. Systems that obey the rules of ordinary logic are special QM systems where a particular choice among the infinite number of complementary QM observables remains sharp for all times, and we insist that those are the only variables we can measure. Viewed in this way, classical physics looks like a sleazy way of dodging the general rules. It achieves a more profound status only because it also emerges as an exponentially good approximation to the behavior of systems with a large number of constituents.
To summarize: All of the so-called non-locality and philosophical mystery of QM is really shared with any probabilistic system of equations and collapse of the wave function is nothing more than application of the conventional rule of conditional probabilities. It is a mistake to think of the wave function as a physical field, like the electromagnetic field. The peculiarity of QM lies in the fact that QM probabilities are intrinsic and not attributable to insufficiently precise measurement, and the fact that they do not obey the law of conditional probabilities. That law is based on the classical logical postulate of the law of the excluded middle. If something is definitely true, then all other independent questions are definitely false. We’ve seen that the mathematical framework for classical logic shows this principle to be erroneous. Even when we’ve specified the state of a system completely, by answering yes or no to every possible question in a compatible set, there are an infinite number of other questions one can ask of the same system, whose answer is only known probabilistically. The formalism predicts a very definite probability distribution for all of these other questions.
Many colleagues who understand everything I’ve said at least as well as I do, are still uncomfortable with the use of probability in fundamental equations. As far as I can tell, this unease comes from two different sources. The first is that the notion of “expectation” seems to imply an expecter, and most physicists are reluctant to put intelligent life forms into the definition of the basic laws of physics. We think of life as an emergent phenomenon, which can’t exist at the level of the microscopic equations. Certainly, our current picture of the very early universe precludes the existence of any form of organized life at that time, simply from considerations of thermodynamic equilibrium.
The frequentist approach to probability is an attempt to get around this. However, its insistence on infinite limits makes it vulnerable to the question about what one concludes about a coin that’s come up heads a million times. We know that’s a possible outcome even if the coin and the flipper are completely honest. Modern experimental physics deals with this problem every day both for intrinsically QM probabilities and those that arise from ordinary random and systematic fluctuations in the detector. The solution is not to claim that any result of measurement is definitely conclusive, but merely to assign a confidence level to each result. Human beings decide when the confidence level is high enough that we “believe” the result, and we keep an open mind about the possibility of coming to a different conclusion with more work. It may not be completely satisfactory from a philosophical point of view, but it seems to work pretty well.
The other kind of professional dissatisfaction with probability is, I think, rooted in Einstein’s prejudice that God doesn’t play dice. With all due respect, I think this is just a prejudice. In the 18th century, certain theoretical physicists conceived the idea that one could, in principle, measure everything there was to know about the universe at some fixed time, and then predict the future. This was wild hubris. Why should it be true? It’s remarkable that this idea worked as well as it did. When certain phenomena appeared to be random, we attributed that to the failure to make measurements that were complete and precise enough at the initial time. This led to the development of statistical mechanics, which was also wildly successful. Nonetheless, there was no real verification of the Laplacian principle of complete predictability. Indeed, when one enquires into the basic physics behind much of classical statistical mechanics one finds that some of the randomness invoked in that theory has a quantum mechanical origin. It arises after all from the motion of individual atoms. It’s no surprise that the first hints that classical mechanics was wrong came from failures of classical statistical mechanics like the Gibbs paradox of the entropy of mixing, and the black body radiation laws.
It seems to me that the introduction of basic randomness into the equations of physics is philosophically unobjectionable, especially once one has understood the inevitability of QM. And to those who find it objectionable all I can say is “It is what it is”. There isn’t anymore. All one must do is account for the successes of the apparently deterministic formalism of classical mechanics when applied to macroscopic bodies, and the theory of decoherence supplies that account.
Perhaps the most important lesson for physicists in all of this is not to mistake our equations for the world. Our equations are an algorithm for making predictions about the world and it turns out that those predictions can only be statistical. That this is so is demonstrated by the simple observation of a
Geiger counter and by the demonstration by Bell and others that the statistical predictions of QM cannot be reproduced by a more classical statistical theory with hidden variables, unless we allow for grossly non-local interactions. Some investigators into the foundations of QM have concluded that we should expect to find evidence for this non-locality, or that QM has to be modified in some fundamental way. I think the evidence all goes in the other direction: QM is exactly correct and inevitable and “there are more things in heaven and earth than are conceived of in our naive classical philosophy”. Of course, Hamlet was talking about ghosts…
Ursus, what preprint is this? Maybe I’m the barbarian for missing it…?
Also, Tom in #14 I’m afraid I still don’t understand what happens in the decoherence picture. Alice measures Particle A, and gets the answer |+>. No matter what, if Bob measures Particle B in the same basis, he must get |->. This is only possible if Particle B *was in |-> state* at the time he measured it. Thus Alice collapsed Bob’s particle to that state.
It doesn’t matter who collapsed it first, but once it is collapsed, *it is collapsed*. Why does discussing the energy microstates of the needle help? I don’t know what you would call this interpretation, but to me the wavefunction is a real thing that collapses instantaneously. Just because that collapse doesn’t transfer any actual information doesn’t mean it isn’t real. The correlations seen in Bell tests, and the loophole tests, seem to show that it collapses, or effectively collapses.
Loving this discussion, by the way!
Note that if we think of the probability function P(x,t) for the hurricane to hit a point x and time t to be a physical field, then this procedure seems non-local or a-causal. The field changes instantaneously to zero at Galveston as soon as we make a measurement in New Orleans. Furthermore, our procedure “violates the weather equations”. Weather evolution seems to have two kinds of dynamics. The deterministic, local, evolution of P(x,t) given by the equation, and the causality violating projection of the probability of Galveston to zero and rescaling of the probability of New Orleans to one, which is mysteriously caused by the measurement process. Recognizing P to be a probability, rather than a physical field, shows that these objections are silly.
My problem with the paragraph quoted here is that the weather equations are not expected to also describe the measurement and rescaling of probabilities. However, Quantum Mechanics, as a complete description of nature is supposed to describe the quantum system as well as the measurement process and the rescaling of probabilities. I suppose the claim is that later on, decoherence and environment-induced superselection (I believe both are necessary) explains how this happens quantum mechanically.
But at this point in the discussion, “these objections are silly” is not justified.
In the classical B,Q ammonia molecule system, how do I measure B? How does the measurement of B affect Q ( not at all?). Isn’t this is rather different from quantum mechanics?
One thing that Tom neglected to mention in his discussion of the exponential size of configuration state space, is that you actually have to create a state space of this exponential size to calculate results with quantum mechanics. How does nature manage to pull off this trick, without also using the informational equivalent of such a massive state space? People wave their hands and hope for quantum computers to perform this magic for them, but to me this indicates that the theory is fundamentally broken as a physical model, right from the start. You don’t even need to talk about EPR or anything fancy to see this. This simply cannot be a description of how nature actually operates, because nature wouldn’t have room for all the information required to perform the necessary calculations (we’re talking 10^(10^80) for all the atoms in the visible universe, for example).
One can trace this problem to the linear nature of the Schrodinger equation: the only way to capture interactions with a linear function is through brute force exponential tensor product space. Yet we know that the Schrodinger model neglects the radiation reaction of electrons onto themselves, which introduces an important source of nonlinearity. Nonlinear systems are much more difficult to analyze, but there is really no justification for thinking you can use a linear equation to model electrons or any other charged particle accurately.
The only sensible conclusion is that, consistent with the main article, this whole edifice is indeed a probability calculus that happens to produce reasonably accurate results, as long as you don’t need the full power of QED, which does model the radiation reaction, but is much more unwieldy compared to the standard QM model — somehow it is always neglected entirely such discussions.
It just seems obvious that, as Einstein believed, there is a more complete, complex, nonlinear model that explains what is actually going on in nature, which happens to reduce to the standard QM probability calculus results under some appropriate simplifying assumptions. At the very least, there is absolutely no reason to think that standard QM accurately describes known physical processes – QED tells us that it manifestly does not. Why does everyone seem to think that it should?
Realized I misread the hurricane example. Its not an example that is the same as QM- but gives a different perspective on collapse of the wave function. So QM results for probabilistic processes with non-commuting observables. I wonder if one can cook up an example in a completely different realm than micro-physics which would have these properties. Like something in the realm of relationships or communication. Does person A love person B for example? If person B tries to determine the answer to this question, it may well affect the outcome. Is there some other less loaded subject (and more able to be made precise) where we might find “observables” that are intrinsically affected by measurement, and then assuming a probabilistic framework can be modeled by quantum mechanics?
Sean asked me to comment on this quote from Tim’s #24
“if one wants to regard
the collapse as merely Bayesian conditionalization, there there has to
be some fact that is being conditionalized on (e.g. the cat being
either alive or dead), and that physical fact ought to be represented
in the physics”
The last phrase here is the key difference between Tim and myself. Tim is trying to use probability in its classical sense i.e. that there are “facts” which exist independent of measurement. I don’t like the word measurement because it implies an intelligent experimenter. For me, any change in what I’ve called a macroscopic quantity is a measurement of something else, which might be another macroscopic quantity,
My point of view is that without such macroscopic changes there doesn’t seem to be any object in the real world that corresponds to what realists want to call facts.
Again, I think it’s extremely important to distinguish between THE REAL WORLD, which in agreement with the realists I think is something that’s out there, independent of our mental processes, and our theory of prediction in the real world. Making the assumption that everything in THE REAL WORLD can be represented by a “fact” in the realist sense contradicts the formalism of quantum mechanics. I’ve argued that if you set up the most general mathematical theory of such facts i.e. mathematical logic, then it also has in it other objects, which can’t be considered facts in this sense. Accepting this requires us to rethink what we mean by probability. To me, Tim’s comment reflects only the original meaning of probability, which was used to talk about an hypothetical world where everything was a fact, but we were merely ignorant of some of the facts.
I’d like to hear a realist comment on a fantasy world in which the fundamental equation of physics was the Langevin equation with a Gaussian random force (say a white noise spectrum, it doesn’t really matter). Langevin interpreted his random force as due to the effect of facts we couldn’t measure, namely random collisions with atoms in a classical model of atoms. I want you to instead assume that experimental investigation has shown that there are no atoms. There’s no mechanical, realist, hidden variable explanation of the random force term.
The mathematical solution of this model is the same as the one in which we postulate that the force comes from atoms, and let us assume it has perfect agreement with experiment, but experiment has shown that there are no atoms, and a bold physicist just says. “Tough, girls and guys, this is the way the world works. The fundamental equations of physics are random.” And let me be clear. I’m not suggesting that there’s some particular fixed time dependent force, which is chosen from the Gaussian probability distribution. I’m suggesting that the correct mathematical procedure for reproducing the results of all experiments is to solve Newton’s equations with a random force and average over the distribution.
I believe that such a theory would be just as objectionable to a realist as my statements about QM. In the fantasy world there would be endless searches for the “source of the randomness” and a complaint that such a theory had no physical facts in it. But I want you to imagine that all such searches had a null result.
QM is much nicer than this, because, with hindsight, we can see that its inevitable randomness is forced on us by mathematical structure that we can’t deny. In Koopman’s formulation of classical mechanics we can define probability distributions for an infinite set of quantities which don’t commute with position and momentum. Every assumed state of the classical system defines these distributions, and their time evolution can be extracted from Schrodinger’s equation.
When Newton et. al. did CM, they were just exploiting the very particular form of the Koopman-Liouville Hamiltonian, which guarantees that the ordinary position and momentum satisfy equations that are independent of the values of all these other observables. But if you pay attention to them, the theory has all of the conceptual subtlety of QM, because it’s just a special form of QM. The analog in our model ammonia molecule is dynamics in discrete time, which simply flips or doesn’t flip s_z from + to -, according to some rule at each time.
So to give the final answer to Tim, I’m conditioning on the life or death of the cat, which, since the cat is a macro=object IS a fact. Fact is an approximate concept. Objective Reality is an Emergent phenomenon. It’s hard for us to accept because our brains weren’t built to understand it.
To all those who uphold quantum theory with the infinite nature hypothesis, I ask 2 questions: What is the physical meaning of the monster group? Are there 6 quarks because there are 6 pariah groups?
arxiv:0312059v4 tells us that there is a theorem by Zurek, 1981, to the effect:
Quote:
“When quantum mechanics is applied to an isolated composite object consisting of a system S and an apparatus A, it cannot determine which observable of the system has been measured.”
#51 Jeff
http://xxx.lanl.gov/abs/1111.3328
Tom,
I think it is worth mentioning that we can not escape the inevitability of the concept of the state. In non-relativistic QM we can readily identify the complete set of commuting observables, which can then be used to define an objects state.
What is more interesting is how this is reflected in the model of the hydrogen atom. A state vector is a continuous function that resides in hilbert space. It is the quantum numbers (the CSCO) that define the apparent shape of this function that we understand as a “real” spatial distribution for the electron clouds.
That reality just tells us where we are likely to witness a photon interact with an electron that has certain quantum numbers. Are the quantum numbers real? We can understand those numbers as being conserved in non-relativistic QM, so they represent information that is somehow stored.
At anyone time though I only have a certain amount of information, and that information can only be consistent with certain states. What we have found out via Bell’s Inequalities, is that all states that are consistent with the information we possess must be evolving in an entangled way. Our observation of the “real” state will provide us with a consistent result, but there is nothing a prior to one’s own observation that will give that state a particular preference over any other.
The possibility that some hidden observer might claim that they were the ones that caused some particular reality before our own observation can only be viewed as an a posterior result that was part of the original set of observational outcomes. Meaning I can not provide any a prior preference to a hidden observer’s view of the world (except to the fact that their observed world will always be perfectly consistent to ones own, once all the information is compared). IOW, it is entirely possible that there is a consistent observation made where there is no hidden observer making wild claims of being the “real” observer.
What is interesting is that this places some weight on the question of free will and choice. To some degree, the world one sees is a “real” manifestation of the choices an observer makes. If we accept that a person’s will is not random (although it should be noted that we can see the choices of a large number of people as at least chaotic, if not purely random), then we have to give weight to the idea that whether a person knows if the cat is dead or not depends on the choice of opening the box. If one chooses not to open the box, then they can be rest assured that there is always some possibility that the cat is alive.
What this all really comes down to is how one manages their time and choices.
#55 Randy
QED is consistent with the Feynman Path Integral formulation of QM which is mathematically equivalent to the Schrödinger “picture” of evolution of the State Vector. The reason we don’t use the Schrödinger “picture” in QED (or any other effective QFT) is that it is impractical to construct/solve the Hamiltonian. This is even difficult in simpler perturbation scenarios with non-relativistic Hamiltonians eg see http://en.wikipedia.org/wiki/Perturbation_theory_%28quantum_mechanics%29
However, in principle, if we could determine the correct (Hilbert) state space and Hamiltonian then QED would be described by the Evolution of a probabilistic State Vector just like in non-relativistic QM.
Intelligibility and reasonableness are lacking in quantum mechanics. The fundamental question is how gravity and inertia fundamentally relate to distance in/of space. Both of these forces must be at half strength/force. As the philosopher Berkeley said, the purpose of vision is to advise of the consequences of touch in time. Invisible and visible space must be balanced, and instantaneity must also be part of the true unification of physics (of quantum gravity, electromagnetism, gravity, and inertia). Opposites must be combined and included.
Tom # 57
We are definitely making some progress in clearing up misunderstandings. If I follow correctly, you have misunderstood the view you are calling “realism”. I take it that, for example, you might as well use Nelson’s stochastic mechanics as your example: there is a fundamentally indeterministic dynamics, not underpinned by any deterministic theory. To my knowledge, absolutely no one who calls themselves a realist, or has trouble with the sorts of claims that are being made here about QM, has any objection or problem at all in such a case. The GRW theory, of course, has an irreducibly random dynamics, and even people working on Bohmian approaches have used irreducible random dynamics. So when you say “I believe that such a theory would be just as objectionable to a realist as my statements about QM”, the statement is just flatly false, and indicates that there has been a fundamental misunderstanding. In stochastic mechanics, even if the dynamics is not deterministic, there is a quite precise set of trajectories that the particles actually follow in any given case, and all macroscopic facts are determined straightforwardly by these microscopic facts: whether the cat in fact ends up alive or dead is a relatively simple function of what the individual particles in the cat do. So it is not true that randomness or indeterminism is inconsistent with what is called “realism”. It is also not true that any indeterministic theory will display the sort of non-locality the Bell worried about: your Langevin equation world will not allow for violations of Bell’s inequality…or in any case, it is trivial to specify local indeterministic theories that do not allow for for violation of the inequalities. So the diagnosis is that somehow realists can’t handle a fundamental failure of determinism is incorrect. But we would like it that the cat ending up alive or dead, which it does, be explicated in terms of what the particles in the cat do, since the cat is nothing more than the sum of its particles. If you say that the individual particles do not end up anywhere in particular, for example, then neither does the cat. So the it can’t be that the only reality is macroscopic reality.
To Tim, and other proponents of a realist stance: perhaps it useful for the rest of us to get a more precise idea of what you mean by the predicate “exist” or the noun “reality”. Tom expresses here very precisely a view that many physicists, like myself, have as a gut feeling. Namely, that any attempt to formalize these notions would necessarily have to rely on some features of classical physics (Tom has identified concretely which features those might be). If so, any attempt to have a “realist interpretation” is secretly an attempt to reduce the quantum to the classical (perhaps with a stochastic element). Do you have any definition of “realism” not relying on the features Tom identifies?
The discussion of the fullness of reality should include/address the following. Instantaneity requires that larger and smaller space (invisible and visible space, and inertia and gravity) be combined, balanced, and included. The balancing/unification of quantum gravity, inertia, electromagnetism, and gravity requires this. Also see my prior post (63) please.
I’m trying to understand in what sense the operator sx corresponds to an “observable” in the classical scenario. Dr. Banks defines it as the *operator* that moves the N atom to the other side of the plane of H atoms (or flips the molecule). What is the operational procedure we would go through to “measure” this “observable”?
If we define the “quantity” B to be just sx, then according to the probability expression stated in the post, P(B) = ½ for “measuring” B to have a value of +1 (or -1). What does this mean physically in the classical scenario?
Also, can anyone give me a good reference for Koopman’s formulation of classical mechanics?
Pingback: Guest Post: David Wallace on the Physicality of the Quantum State | Cosmic Variance | Discover Magazine
Pingback: Interpretation of Quantum Mechanics in the News | Quantum Mechanics Blog
This note says superpositions are not possible in classical mechanics, even with Koopman’s tricks: http://prl.aps.org/abstract/PRL/v105/i15/e150604
Arxiv: http://arxiv.org/abs/1006.3029
#62 Gallagher:
But isn’t it the very nonlinearity of the self-field coupling (i.e., virtual particle loops) in QED that make it impossible to use in the standard QM picture? Seems to me that this “impracticality” may be pointing to the deeper issue that the standard Hilbert space depends on linearity and nature just doesn’t work that way. It is a polite fiction, which seems to be leading us astray?
#71 Randy
the nonlinearities are emergent from the (complicated) linear evolution. Otherwise you would have a simple argument to debunk MWI for example.
Moshe # 65
I think that this discussion of the terms “real” and “exist”, and even the term “realist” is rather backwards. It is not that “realists” think that these are interesting terms in need of some fancy definition. “Real” and “exist” are typically redundant: thus “I own a car”, “I own a real car”, “I own a car that really exists”, “I, who exist, really own a real car that really exists in reality” all say exactly the same same thing. As a philosopher says, they have the same truth conditions. And “I own a car” does not use the terms “real” or “exist”, so they play no substantial role.
What “realists” want is simple: they want a physical theory to state clearly an unambiguously exactly what it postulates, and the laws (deterministic or probabilistic) that describe how what it postulates behaves. Anything short of that just isn’t a physical theory. It may be good advice about how to bet in certain circumstances (in which case it at least postulates the existence of the circumstance!), but it isn’t a physical theory of those things.
There are cats. Cats are real. Real cats exists. These all say the same thing. Cats are macroscopic items: you can see them with your naked eye. They are made up out of microscopic parts. All the “realist” wants to to know what those parts are, and how they behave. If you say: “cats exist, but the ’emerge’ out of things that don’t exist”, that makes no sense: nothing can “emerge” out of what doesn’t exist, since there is nothing to emerge out of.
Banks’s view seems to be this: there is some microscopic reality, some small parts that make up cats, but we a incapable of comprehending them. That is a possible view, but I fail to see any argument that suggests it is correct. There certainly are clear, comprehensible physical theories that predict exactly the behavior at a macroscopic scale that is predicted by quantum theory. So there is nothing in the empirical predictions that rules out a comprehensible account of the physical world.
Tim, thanks for your response. We might have reached a point of mutual incomprehension (not uncommon in this medium), but let me try one more iteration.
To understand where I am coming from let me make an analogy to the crisis in the foundations of mathematics in the early 20th century. In that case people asked questions (about the set of all sets and so forth) that made complete intuitive sense at the level of natural language, but did not have self-consistent answers. This was resolved only after a systematic effort to formalize the foundations of the subject. Part of the result was the clarification of which natural language questions were “askable”, many of them aren’t.
Keeping with this analogy, and given that quantum mechanics (as far as we know) is a precise, consistent and complete mathematical framework, the natural reaction to a set of confusing natural language questions is that these may not be “askable” in the same sense — they certainly don’t seem to be well-formed questions within the framework of conventional quantum mechanics (for reasons that Tom points out). Maybe that is reason to doubt conventional QM, but I am wondering if anything short of return to some form of classical mechanics can be deemed to be “realist”.
Moshe
I don’t think that the foundational issues in set theory were resolved in the way you suggest. The problem wasn’t in natural language or in what questions “can be asked”: the problem was that the axioms of naive set theory were demonstrably inconsistent (implied a contradiction). And the fix was not to somehow restrict the language, much less to revise the logic used in the derivation: the fix was to change the axioms (to, for example, ZFC). I don’t know what questions in set theory you think are not “askable”. An example here would help.
Quantum mechanics uses mathematics, and in many cases (though not all: for example saying that collapse occurs when a measurement occurs) the way to use the mathematics is precise. But neither quantum mechanics, not any other physical theory, is just a piece of mathematics. The mathematics is supposed to be used to describe or represent some physical reality, and one want to know how that is done.
For example, the EPR paper asks a simple question about the mathematical wavefunction used in QM: is it complete, that is, does specifying the wavefunction specify (one way or another) all of the physical characteristics of a system? Einstein et. al argued no, in which it follows that a complete physical specification of system requires more variables (usually incorrectly called “hidden variables”). The mainstream of physics rejected that idea, in part mistakenly believing that von Neumann had proven it not to be possible. So this is a clear question to ask of any physical understanding of the mathematical quantum formalism: is the wavefunction, according to this understanding, a complete physical description or not? If you can’t clearly answer this question, then you have not got a clear physical theory.
It seems to me that Banks is committed to saying the that wavefunction is not complete. It is only such a view that can make sense of the “collapse” of the wavefunction as merely Bayesian conditionalization. That is, if the wavefunction of a system does not completely specify its physical state, then it is possible to find out new information about the physical state even given the wavefunction, and then to update your information about the system. But if the wavefunction is complete, and you already know what it is (e.g. for an pair of electrons in the singlet state), then there just isn’t anything more to know, and changing the representation of the wavefunction by collapse must indicate and actual physical change in the system. But if the wavefunction is not complete, and there is more to the physical state of a pair of particles in an singlet state than can be derived from the singlet state, then as a matter of physics we want to know what these additional physical degrees of freedom are and how they behave.
Studying the mathematics used to represent the wavefunction simply does not address any of these physical questions. It is not the mathematics per se but the use of the mathematics in the service of physics that is in questions. So we might begin here: take a pair of electrons in an singlet state and send one off to Pluto. We know what the wavefunction will be when it gets to Pluto, and that (e.g.) the wavefunction does not attribute a particular spin in any direction to either of the particles. So: do you think this is a complete physical description, and the electron has no definite spin, or not a complete description? Only with a clear answer to such a question can we begin to see how you are using the mathematical formalism to do physics.