The lure of blogging is strong. Having guest-posted about problems with eternal inflation, Tom Banks couldn’t resist coming back for more punishment. Here he tackles a venerable problem: the interpretation of quantum mechanics. Tom argues that the measurement problem in QM becomes a lot easier to understand once we appreciate that even classical mechanics allows for non-commuting observables. In that sense, quantum mechanics is “inevitable”; it’s actually classical physics that is somewhat unusual. If we just take QM seriously as a theory that predicts the probability of different measurement outcomes, all is well.
Tom’s last post was “technical” in the sense that it dug deeply into speculative ideas at the cutting edge of research. This one is technical in a different sense: the concepts are presented at a level that second-year undergraduate physics majors should have no trouble following, but there are explicit equations that might make it rough going for anyone without at least that much background. The translation from LaTeX to WordPress is a bit kludgy; here is a more elegant-looking pdf version if you’d prefer to read that.
—————————————-
Rabbi Eliezer ben Yaakov of Nahariya said in the 6th century, “He who has not said three things to his students, has not conveyed the true essence of quantum mechanics. And these are Probability, Intrinsic Probability, and Peculiar Probability”.
Probability first entered the teachings of men through the work of that dissolute gambler Pascal, who was willing to make a bet on his salvation. It was a way of quantifying our risk of uncertainty. Implicit in Pascal’s thinking, and all who came after him was the idea that there was a certainty, even a predictability, but that we fallible humans may not always have enough data to make the correct predictions. This implicit assumption is completely unnecessary and the mathematical theory of probability makes use of it only through one crucial assumption, which turns out to be wrong in principle but right in practice for many actual events in the real world.
For simplicity, assume that there are only a finite number of things that one can measure, in order to avoid too much math. List the possible measurements as a sequence
![]()
The aN are the quantities being measured and each could have a finite number of values. Then a probability distribution assigns a number P(A) between zero and one to each possible outcome. The sum of the numbers has to add up to one. The so called frequentist interpretation of these numbers is that if we did the same measurement a large number of times, then the fraction of times or frequency with which we’d find a particular result would approach the probability of that result in the limit of an infinite number of trials. It is mathematically rigorous, but only a fantasy in the real world, where we have no idea whether we have an infinite amount of time to do the experiments. The other interpretation, often called Bayesian, is that probability gives a best guess at what the answer will be in any given trial. It tells you how to bet. This is how the concept is used by most working scientists. You do a few experiments and see how the finite distribution of results compares to the probabilities, and then assign a confidence level to the conclusion that a particular theory of the data is correct. Even in flipping a completely fair coin, it’s possible to get a million heads in a row. If that happens, you’re pretty sure the coin is weighted but you can’t know for sure.
Physical theories are often couched in the form of equations for the time evolution of the probability distribution, even in classical physics. One introduces “random forces” into Newton’s equations to “approximate the effect of the deterministic motion of parts of the system we don’t observe”. The classic example is the Brownian motion of particles we see under the microscopic, where we think of the random forces in the equations as coming from collisions with the atoms in the fluid in which the particles are suspended. However, there’s no a priori reason why these equations couldn’t be the fundamental laws of nature. Determinism is a philosophical stance, an hypothesis about the way the world works, which has to be subjected to experiment just like anything else. Anyone who’s listened to a geiger counter will recognize that the microscopic process of decay of radioactive nuclei doesn’t seem very deterministic.
The place where the deterministic hypothesis and the laws of classical logic are put into the theory of probability is through the rule for combining probabilities of independent alternatives. A classic example is shooting particles through a pair of slits. One says, “the particle had to go through slit A or slit B and the probabilities are independent of each other, so,
![]()
It seems so obvious, but it’s wrong, as we’ll see below. The probability sum rule, as the previous equation is called, allows us to define conditional probabilities. This is best understood through the example of hurricane Katrina. The equations used by weather forecasters are probabilistic in nature. Long before Katrina made landfall, they predicted a probability that it would hit either New Orleans or Galveston. These are, more or less, mutually exclusive alternatives. Because these weather probabilities, at least approximately, obey the sum rule, we can conclude that the prediction for what happens after we make the observation of people suffering in the Superdome, doesn’t depend on the fact that Katrina could have hit Galveston. That is, that observation allows us to set the probability that it could have hit Galveston to zero, and re-scale all other probabilities by a common factor so that the probability of hitting New Orleans was one.
Note that if we think of the probability function P(x,t) for the hurricane to hit a point x and time t to be a physical field, then this procedure seems non-local or a-causal. The field changes instantaneously to zero at Galveston as soon as we make a measurement in New Orleans. Furthermore, our procedure “violates the weather equations”. Weather evolution seems to have two kinds of dynamics. The deterministic, local, evolution of P(x,t) given by the equation, and the causality violating projection of the probability of Galveston to zero and rescaling of the probability of New Orleans to one, which is mysteriously caused by the measurement process. Recognizing P to be a probability, rather than a physical field, shows that these objections are silly.
Nothing in this discussion depends on whether we assume the weather equations are the fundamental laws of physics of an intrinsically uncertain world, or come from neglecting certain unmeasured degrees of freedom in a completely deterministic system.
The essence of QM is that it forces us to take an intrinsically probabilistic view of the world, and that it does so by discovering an unavoidable probability theory underlying the mathematics of classical logic. In order to describe this in the simplest possible way, I want to follow Feynman and ask you to think about a single ammonia molecule, NH3. A classical picture of this molecule is a pyramid with the nitrogen at the apex and the three hydrogens forming an equilateral triangle at the base. Let’s imagine a situation in which the only relevant measurement we could make was whether the pyramid was pointing up or down along the z axis. We can ask one question Q, “Is the pyramid pointing up?” and the molecule has two states in which the answer is either yes or no. Following Boole, we can assign these two states the numerical values 1 and 0 for Q, and then the “contrary question” 1 − Q has the opposite truth values. Boole showed that all of the rules of classical logic could be encoded in an algebra of independent questions, satisfying
![]()
where the Kronecker symbol δij = 1 if i = j and 0 otherwise. i,j run from 1 to N, the number of independent questions. We also have ∑Qi = 1, meaning that one and only one of the questions has the answer yes in any state of the system. Our ammonia molecule has only two independent questions, Q and 1 − Q. Let me also define sz = 2Q − 1 = ±1, in the two different states. Computer aficionadas will recognize our two question system as a bit.
We can relate this discussion of logic to our discussion of probability of measurements by introducing observables A = ∑ai Qi , where the ai are real numbers, specifying the value of some measurable quantity in the state where only Qi has the answer yes. A probability distribution is then just a special case ρ = ∑pi Qi, where pi is non-negative for each i and ∑pi = 1.
Restricting attention to our ammonia molecule, we denote the two states as | ±z 〉 and summarize the algebra of questions by the equation
![]()
We say that ” the operator sz acting on the states | ±z 〉 just multiplies them by (the appropriate ) number”. Similarly, if A = a+ Q + a− (1 − Q) then
![]()
The expected value of the observable An in the probability distribution ρ is
![]()
In the last equation we have used the fact that all of our “operators” can be thought of as two by two matrices acting on a two dimensional space of vectors whose basis elements are |±z 〉. The matrices can be multiplied by the usual rules and the trace of a matrix is just the sum of its diagonal elements. Our matrices are
![]()
![]()
![]()
![]()
They’re all diagonal, so it’s easy to multiply them.
So far all we’ve done is rewrite the simple logic of a single bit as a complicated set of matrix equations, but consider the operation of flipping the orientation of the molecule, which for nefarious purposes we’ll call sx,
![]()
This has matrix
![]()
Note that sz2 = sx2 = 1, and sx sz = − sz sx = − i sy , where the last equality is just a definition. This definition implies that sy sa = − sa sy, for a = x or a = z, and it follows that sy2 = 1. You can verify these equations by using matrix multiplication, or by thinking about how the various operations operate on the states (which I think is easier). Now consider for example the quantity B ≡ bx sx + bz sz . Then B2 = bx2 + bz2 , which suggests that B is a quantity which takes on the possible values ±√{b+2 + b−2}. We can calculate
![]()
for any choice of probability distribution. If n = 2k it’s just
![]()
whereas if n = 2k + 1 it’s
![]()
This is exactly the same result we would get if we said that there was a probability P+ (B) for B to take on the value √{bz2 + bx2} and probability P− (B) = 1 − P+ (B), to take on the opposite value, if we choose
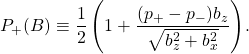
The most remarkable thing about this formula is that even when we know the answer to Q with certainty (p+ = 1 or 0), B is still uncertain.
We can repeat this exercise with any linear combination bx sx + by sy + bz sz. We find that in general, if we force one linear combination to be known with certainty, that all linear combinations where the vector (cx, cy, cz) is not parallel to (bx , by, bz) are uncertain. This is the same as the condition guaranteeing that the two linear combinations commute as matrices.
Pursuing the mathematics of this further would lead us into the realm of eigenvalues of Hermitian matrices, complete ortho-normal bases and other esoterica. But the main point to remember is that any system we can think about in terms of classical logic inevitably contains in it an infinite set of variables in addition to the ones we initially thought about as the maximum set of things we thought could be measured. When our original variables are known with certainty, these other variables are uncertain but the mathematics gives us completely determined formulas for their probability distributions.
Another disturbing fact about the mathematical probability theory for non-compatible observables that we’ve discovered, is that it does NOT satisfy the probability sum rule. This is because, once we start thinking about incompatible observables, the notion of either this or that is not well defined. In fact we’ve seen that when we know “definitely for sure” that sz is 1, the probability for B to take on its positive value could be any number between zero and one, depending on the ratio of bz and bx.
Thus QM contains questions that are neither independent nor dependent and the probability sum rule P(sz or B ) = P(sz) + P(B) does not make sense because the word or is undefined for non-commuting operators. As a consequence we cannot apply the conditional probability rule to general QM probability predictions. This appears to cause a problem when we make a measurement that seems to give a definite answer. We’ll explain below that the issue here is the meaning of the word measurement. It means the interaction of the system with macroscopic objects containing many atoms. One can show that conditional probability is a sensible notion, with incredible accuracy, for such objects, and this means that we can interpret QM for such objects as if it were a classical probability theory. The famous “collapse of the wave function” is nothing more than an application of the rules of conditional probability, to macroscopic objects, for which they apply.
The double slit experiment famously discussed in the first chapter of Feynman’s lectures on quantum mechanics, is another example of the failure of the probability sum rule. The question of which slit the particle goes through is one of two alternative histories. In Newton’s equations, a history is determined by an initial position and velocity, but Heisenberg’s famous uncertainty relation is simply the statement that position and velocity are incompatible observables, which don’t commute as matrices, just like sz and sx. So the statement that either one history or another happened does not make sense, because the two histories interfere.
Before leaving our little ammonia molecule, I want to tell you about one more remarkable fact, which has no bearing on the rest of the discussion, but shows the remarkable power of quantum mechanics. Way back at the top of this post, you could have asked me, “what if I wanted to orient the ammonia along the x axis or some other direction”. The answer is that the operator nx sx + ny sy + nz sz, where (nx , ny, nz) is a unit vector, has definite values in precisely those states where the molecule is oriented along this unit vector. The whole quantum formalism of a single bit, is invariant under 3 dimensional rotations. And who would have ever thought of that? (Pauli, that’s who).
The fact that QM was implicit in classical physics was realized a few years after the invention of QM, in the 1930s, by Koopman. Koopman formulated ordinary classical mechanics as a special case of quantum mechanics, and in doing so introduced a whole set of new observables, which do not commute with the (commuting) position and momentum of a particle and are uncertain when the particle’s position and momentum are definitely known. The laws of classical mechanics give rise to equations for the probability distributions for all these other observables. So quantum mechanics is inescapable. The only question is whether nature is described by an evolution equation which leaves a certain complete set of observables certain for all time, and what those observables are in terms of things we actually measure. The answer is that ordinary positions and momenta are NOT simultaneously determined with certainty.
Which raises the question of why it took us so long to notice this, and why it’s so hard for us to think about and accept. The answers to these questions also resolve “the problem of quantum measurement theory”. The answer lies essentially in the definition of a macroscopic object. First of all it means something containing a large number N of microscopic constituents. Let me call them atoms, because that’s what’s relevant for most everyday objects. For even a very tiny piece of matter weighing about a thousandth of a gram, the number N ∼ 1020. There are a few quantum states of the system per atom, let’s say 10 to keep the numbers round. So the system has 101020 states. Now consider the motion of the center of mass of the system. The mass of the system is proportional to N, so Heisenberg’s uncertainty relation tells us that the mutual uncertainty of the position and velocity of the system is of order [1/N]. Most textbooks stop at this point and say this is small and so the center of mass behaves in a classical manner to a good approximation.
In fact, this misses the central point, which is that under most conditions, the system has of order 10N different states, all of which have the same center of mass position and velocity (within the prescribed uncertainty). Furthermore the internal state of the system is changing rapidly on the time scale of the center of mass motion. When we compute the quantum interference terms between two approximately classical states of the center of mass coordinate, we have to take into account that the internal time evolution for those two states is likely to be completely different. The chance that it’s the same is roughly 10−N, the chance that two states picked at random from the huge collection, will be the same. It’s fairly simple to show that the quantum interference terms, which violate the classical probability sum rule for the probabilities of different classical trajectories, are of order 10−N. This means that even if we could see the [1/N] effects of uncertainty in the classical trajectory, we could model them by ordinary classical statistical mechanics, up to corrections of order 10−N.
It’s pretty hard to comprehend how small a number this is. As a decimal, it’s a decimal point followed by 100 billion billion zeros and then a one. The current age of the universe is less than a billion billion seconds. So if you wrote one zero every hundredth of a second you couldn’t write this number in the entire age of the universe. More relevant is the fact that in order to observe the quantum interference effects on the center of mass motion, we would have to do an experiment over a time period of order 10N. I haven’t written the units of time. The smallest unit of time is defined by Newton’s constant, Planck’s constant and the speed of light. It’s 10− 44 seconds. The age of the universe is about 1061 of these Planck units. The difference between measuring the time in Planck times or ages of the universe is a shift from N = 1020 to N = 1020 − 60, and is completely in the noise of these estimates. Moreover, the quantum interference experiment we’re proposing would have to keep the system completely isolated from the rest of the universe for these incredible lengths of time. Any coupling to the outside effectively increases the size of N by huge amounts.
Thus, for all purposes, even those of principle, we can treat quantum probabilities for even mildly macroscopic variables, as if they were classical, and apply the rules of conditional probability. This is all we are doing when we “collapse the wave function” in a way that seems (to the untutored) to violate causality and the Schrodinger equation. The general line of reasoning outlined above is called the theory of decoherence. All physicists find it acceptable as an explanation of the reason for the practical success of classical mechanics for macroscopic objects. Some physicists find it inadequate as an explanation of the philosophical “paradoxes” of QM. I believe this is mostly due to their desire to avoid the notion of intrinsic probability, and attribute physical reality to the Schrodinger wave function. Curiously many of these people think that they are following in the footsteps of Einstein’s objections to QM. I am not a historian of science but my cursory reading of the evidence suggests that Einstein understood completely that there were no paradoxes in QM if the wave function was thought of merely as a device for computing probability. He objected to the contention of some in the Copehagen crowd that the wave function was real and satisfied a deterministic equation and tried to show that that interpretation violated the principles of causality. It does, but the statistical treatment is the right one. Einstein was wrong only in insisting that God doesn’t play dice.
Once we have understood these general arguments, both quantum measurement theory and our intuitive unease with QM are clarified. A measurement in QM is, as first proposed by von Neumann, simply the correlation of some microscopic observable, like the orientation of an ammonia molecule, with a macro-observable like a pointer on a dial. This can easily be achieved by normal unitary evolution. Once this correlation is made, quantum interference effects in further observation of the dial are exponentially suppressed, we can use the conditional probability rule, and all the mystery is removed.
It’s even easier to understand why humans don’t “get” QM. Our brains evolved according to selection pressures that involved only macroscopic objects like fruit, tigers and trees. We didn’t have to develop neural circuitry that had an intuitive feel for quantum interference phenomena, because there was no evolutionary advantage to doing so. Freeman Dyson once said that the book of the world might be written in Jabberwocky, a language that human beings were incapable of understanding. QM is not as bad as that. We CAN understand the language if we’re willing to do the math, and if we’re willing to put aside our intuitions about how the world must be, in the same way that we understand that our intuitions about how velocities add are only an approximation to the correct rules given by the Lorentz group. QM is worse, I think, because it says that logic, which our minds grasp as the basic, correct formulation of rules of thought, is wrong. This is why I’ve emphasized that once you formulate logic mathematically, QM is an obvious and inevitable consequence. Systems that obey the rules of ordinary logic are special QM systems where a particular choice among the infinite number of complementary QM observables remains sharp for all times, and we insist that those are the only variables we can measure. Viewed in this way, classical physics looks like a sleazy way of dodging the general rules. It achieves a more profound status only because it also emerges as an exponentially good approximation to the behavior of systems with a large number of constituents.
To summarize: All of the so-called non-locality and philosophical mystery of QM is really shared with any probabilistic system of equations and collapse of the wave function is nothing more than application of the conventional rule of conditional probabilities. It is a mistake to think of the wave function as a physical field, like the electromagnetic field. The peculiarity of QM lies in the fact that QM probabilities are intrinsic and not attributable to insufficiently precise measurement, and the fact that they do not obey the law of conditional probabilities. That law is based on the classical logical postulate of the law of the excluded middle. If something is definitely true, then all other independent questions are definitely false. We’ve seen that the mathematical framework for classical logic shows this principle to be erroneous. Even when we’ve specified the state of a system completely, by answering yes or no to every possible question in a compatible set, there are an infinite number of other questions one can ask of the same system, whose answer is only known probabilistically. The formalism predicts a very definite probability distribution for all of these other questions.
Many colleagues who understand everything I’ve said at least as well as I do, are still uncomfortable with the use of probability in fundamental equations. As far as I can tell, this unease comes from two different sources. The first is that the notion of “expectation” seems to imply an expecter, and most physicists are reluctant to put intelligent life forms into the definition of the basic laws of physics. We think of life as an emergent phenomenon, which can’t exist at the level of the microscopic equations. Certainly, our current picture of the very early universe precludes the existence of any form of organized life at that time, simply from considerations of thermodynamic equilibrium.
The frequentist approach to probability is an attempt to get around this. However, its insistence on infinite limits makes it vulnerable to the question about what one concludes about a coin that’s come up heads a million times. We know that’s a possible outcome even if the coin and the flipper are completely honest. Modern experimental physics deals with this problem every day both for intrinsically QM probabilities and those that arise from ordinary random and systematic fluctuations in the detector. The solution is not to claim that any result of measurement is definitely conclusive, but merely to assign a confidence level to each result. Human beings decide when the confidence level is high enough that we “believe” the result, and we keep an open mind about the possibility of coming to a different conclusion with more work. It may not be completely satisfactory from a philosophical point of view, but it seems to work pretty well.
The other kind of professional dissatisfaction with probability is, I think, rooted in Einstein’s prejudice that God doesn’t play dice. With all due respect, I think this is just a prejudice. In the 18th century, certain theoretical physicists conceived the idea that one could, in principle, measure everything there was to know about the universe at some fixed time, and then predict the future. This was wild hubris. Why should it be true? It’s remarkable that this idea worked as well as it did. When certain phenomena appeared to be random, we attributed that to the failure to make measurements that were complete and precise enough at the initial time. This led to the development of statistical mechanics, which was also wildly successful. Nonetheless, there was no real verification of the Laplacian principle of complete predictability. Indeed, when one enquires into the basic physics behind much of classical statistical mechanics one finds that some of the randomness invoked in that theory has a quantum mechanical origin. It arises after all from the motion of individual atoms. It’s no surprise that the first hints that classical mechanics was wrong came from failures of classical statistical mechanics like the Gibbs paradox of the entropy of mixing, and the black body radiation laws.
It seems to me that the introduction of basic randomness into the equations of physics is philosophically unobjectionable, especially once one has understood the inevitability of QM. And to those who find it objectionable all I can say is “It is what it is”. There isn’t anymore. All one must do is account for the successes of the apparently deterministic formalism of classical mechanics when applied to macroscopic bodies, and the theory of decoherence supplies that account.
Perhaps the most important lesson for physicists in all of this is not to mistake our equations for the world. Our equations are an algorithm for making predictions about the world and it turns out that those predictions can only be statistical. That this is so is demonstrated by the simple observation of a
Geiger counter and by the demonstration by Bell and others that the statistical predictions of QM cannot be reproduced by a more classical statistical theory with hidden variables, unless we allow for grossly non-local interactions. Some investigators into the foundations of QM have concluded that we should expect to find evidence for this non-locality, or that QM has to be modified in some fundamental way. I think the evidence all goes in the other direction: QM is exactly correct and inevitable and “there are more things in heaven and earth than are conceived of in our naive classical philosophy”. Of course, Hamlet was talking about ghosts…
I don’t think most people who are concerned about the measurement problem are concerned about determinism. Rather, they are concerned about realism, i.e. the idea that there is something out there that exists independently of observers. If you want to be a realist then it is not so easy to pass off the quantum state as something akin to a probability distribution. See this recent preprint:
http://arxiv.org/abs/1111.3328
for a simple demonstration of this.
Good post. Apparently the “Gibbs Paradox” isn’t really a paradox and failure of classical stat. mech. though: http://bayes.wustl.edu/etj/articles/gibbs.paradox.pdf
Very enlightening post! Can Tom or someone else who grasps the math elucidate if and how the arguments espoused here pertain to quantum entanglement-was Einstein wrong to consider such apparent non-locality ‘spooky action at a distance’ as he was in stating that ‘God does not play dice?’
Rabbi Eliezer ben Yaakov = Eliezer Yudkowsky? (In which case: why Nahariya?) Or is there some actual 6th-century rabbi who said something about three things students ought to be taught? (In which case: who and what? Google doesn’t seem to know.)
Note that if we think of the probability function P(x,t) for the hurricane to hit a point x and time t to be a physical field, then this procedure seems non-local or a-causal. The field changes instantaneously to zero at Galveston as soon as we make a measurement in New Orleans. Furthermore, our procedure “violates the weather equations”. Weather evolution seems to have two kinds of dynamics. The deterministic, local, evolution of P(x,t) given by the equation, and the causality violating projection of the probability of Galveston to zero and rescaling of the probability of New Orleans to one, which is mysteriously caused by the measurement process.
If you make the prediction on Sunday for where the hurricane might be on Wednesday, then your Wednesday measurement does this seemingly non-local or a-causal rescaling of probabilities. But if you make the prediction on Sunday 5 PM about where the hurricane might be at 5:01 PM, there is no non-locality or a-causality apparent when you make the measurement at 5:01 PM.
—
“The most remarkable thing about this formula is that even when we know the answer to Q with certainty (p+ = 1 or 0), B is still uncertain.”
Though B is uncertain, you can measure Q and B together, can you not? If Q is known with certainty, then measuring B first does not change Q, I suppose. In quantum mechanics, measuring B first will throw Q into a state of uncertainty, even if the initial state was prepared with a definite Q?
Unfortunately, the understanding of the interpretive difficulties of quantum mechanics in this article is incorrect, so the discussion does not touch the important issues. The measurement problem of standard quantum mechanics has nothing at all to do with the observability or unobservability of interference in macroscopic systems, so consideration of how decoherence can suppress interference does nothing to solve the problem. Anyone reading Schrödinger’s original “cat” paper can see that possible interference is not among the issues he discusses. He is rather concerned about how the cat ends up either alive or dead. If one wants to have the outcome be due to an irreducibly stochastic dynamics, fine: then explain clearly what the possible physical states of the system are and provide a stochastic evolution law for those states. Banks apparently agrees with the contention of the EPR paper that the wavefunction does not provide a complete physical description. Then what does? This is not asking for determinism: the dynamics can be as indeterministic as you like. It is asking for a clear physical theory.
The discussion of non-locality and Bell is completely off-target. Einstein was not worried about indeterminism or “God playing dice”: he was worried about the evident non-locality of the standard theory with collapse if one takes the wavefunction to be complete. Thus the title of the EPR paper. If one wants to avoid the non-locality, as EPR correctly argues, then the results of (e.g.) spin measurements must be predetermined by local state of the particles measured. But any such predetermination, together with a prohibition on non-local effects, implies that Bell inequality cannot be violated. What Bell proved is that no local theory can reproduce the predictions of QM. To suggest that the non-locality is merely an apparent effect of conditionalization shows that one has not understood Bell at all: see his discussion of Bertlmann’s socks.
“All physicists find it [decoherence] acceptable as an explanation of the reason for the practical success of classical mechanics for macroscopic objects”.
Really? I’m sure I’ve seen objections to it.
The unsatisfying philosophical aspect is that you leave macroscopic states still in a superposition, with no way of ever resolving it, whether or not they can interfere with each other.
And, can’t you get at that superposition by making it have effects back in the microworld?
Suppose I observe Schrodinger’s cat alive or dead (or count clicks from a Geiger counter, whatever). So according to decoherence theory that now puts my brain (and any part of the world my actions influence) into a superposition, but I can’t observe interference effects because the state vector of my brain has too many dimensions to ever get the two states to line up.
So, now I walk across the room, and depending on how I saw the cat, close one or other of the slits in a two-slit experiment. Shouldn’t I now see an interference pattern on the screen, in violation of presumably everyone’s expectations? We can put the necessary laser in as fancy an isolating box as you need so that it isn’t affected by my thought processes or manipulation of the slits.
I don’t get what the ammonia example is supposed to demonstrate at all:
So, we take the system either definitely up or down (Q). Then we do some junk with matrices, which are all still completely defined, and then we define B in terms of coefficients b_x and b_z that we just made up. Then we act surprised that the value we get for B depends on the coefficients we put in?
I mean this is how classical mechanics works in that if you take a known number and multiply it by random factors you get a random number. But it’s nothing to do with how the quantum mechanics of spin works (there s_x and s_y really do represent the two other directions and the issue is that they aren’t allowed to take on the intermediate values you’d want when you observe them).
Tom,
Am hopeful you can clarify/explain a couple of things.
As you point out, a small macroscopic system of N atoms has order 10^N relevant states, assuming ~10 relevant states per atom. Let’s say this system is a measuring device. Now assume you have prepared a pure superposition state involving at most a few particles in an ultra-cold environment, carefully designing the experiment to isolate the prepared superposition from interference with the apparatus and the rest of the environment.
Finally, you make a measurement to resolve the superposition, i.e., induce a “wave function collapse” in the usual interpretation. It seems you argue there is nothing like a wave function collapse, just an interaction with the macroscopic system of order 10^N states that behaves classically due to exponential suppression of quantum interference effects. (This last statement is probably a bit of an oversimplification of your view, but hopefully it captures the spirit.)
Now for the questions. Chris (#7) mentions some already, for which I look forward to seeing answers. A couple of others are below, following their context.
1. Surely the measuring device (and other parts of the apparatus, especially the part that prepared the superposition in the first place) must in some sense be considered part of the same quantum system as the superposition undergoing measurement; otherwise, how could the measuring device interact with it in a way consistent with quantum mechanics? But the measuring device, superposition-preparation subsystem, and superposition undergoing measurement must largely factor, or else there is no separation between “measurer” and “measured” that would make a “measurement” mean something.
The question: In the decoherence picture, how does the essentially classical apparatus (so deemed because it has “gobs” of atoms) produce a quantum mechanical superposition in a very predictable manner, i.e., through progression from the classical to quantum? Especially, is the exponential suppression of quantum interference effects at all relevant here? (I’m struggling to phrase this question clearly, so I’ll understand if you don’t know what I’m getting at.)
2. For at least some kinds of measurements, the interaction with the apparatus will need to be highly localized, maybe even to a single atom initially (but amplified by further interactions with neighboring atoms, e.g., by cascading effects, until the “measurement event” becomes macroscopically detectable). I’m not clear how such a localized interaction (e.g., with one to tens of atoms) can take advantage of the 10^N states of the measuring device to avoid a wave function collapse picture. For example, I think cascading effects can be viewed classically, e.g., one electron knocks an electron free from multiple atoms after being accelerated in a classical electric field, so a classical picture would seem to arise long before anywhere close to N atoms are involved.
The questions: At what point does decoherence become prominent when initial interaction with the measuring device is highly localized? How does the wave function of the superposition evolve during this time if it doesn’t “collapse” after the interaction, and is this evolution reversible in some sense (as opposed to collapse, which would not be reversible)?
Tim Maudlin #6: The view that I take Banks to be defending here is actually one I’ve found extremely common among physicists, so maybe it would be worth philosophers trying to understand it sympathetically and seeing how much sense they can make of it. I like to think of this view as “Many Worlds minus the Many Worlds” — i.e., many worlds without calling it that, or even acknowledging a need to discuss that apparent implication of what you’re saying. On the one hand, you view a measurement as just an ordinary, unitary physical interaction, albeit one that “looks and smells measurement-like”—i.e., that exponentially suppresses the off-diagonal terms in a suitable density matrix, because of decoherence theory. On the other hand, you view the reduction of the state vector as completely analogous to ordinary Bayesian conditioning. What are you conditioning on, in this case? Well, presumably, which block of the now-block-diagonal density matrix you’re now “in”! So basically, you get to play a double game: treating the state vector “realistically” for the purpose of understanding unitary evolution (including the entanglement of the system and measuring device that causes decoherence), but then “ontologically” for the final step of the Born rule and state-vector reduction. The gap—i.e., the obvious disanalogies between what we’re doing now and ordinary Bayesian conditioning—are bridged over by
(1) stressing just how drastically the macroscopic interference terms are suppressed, and therefore how unlikely it is that we’ll ever run into problems in practice, and
(2) saying “well, this is quantum mechanics, a perfectly-natural non-commutative generalization of ordinary Bayesian probability theory. If you find it unintuitive, then the problem is with your intuition.”
Chris #7: Alas, your proposed experiment doesn’t work (which is a pity, because otherwise we could presumably use it to distinguish different interpretations of quantum mechanics!). If your brain is in a different state depending on which measurement outcome you saw, that will already be enough to prevent an interference pattern, according to the standard rules of QM. (Nothing special about your brain here: everything else in the entire universe needs to be the same in states S1 and S2 in order to observe interference between them. That’s why building a quantum computer and other quantum-mechanical experiments are so hard!)
OXO #9: Rabbi Mordecai ben Aharon of Mitzpe Ramon told his disciplines, “he who cannot skim past a fizzled, groan-inducing introductory joke to get to the meat, will not get far in his studies of quantum physics.”
I’m sympathetic to Tim Maudlin’s complaints about the post, but have a somewhat different perspective.
Banks seems to say that physicists start to go astray when they try to “attribute physical reality to the Schrodinger wave function.” Tim might agree with this aspect of Tom’s post. I believe the opposite is true.
A new paper entitled “The quantum state can not be interpreted statistically” (See: http://arxiv.org/PS_cache/arxiv/pdf/1111/1111.3328v1.pdf), clearly highlights this issue.
The authors conclude that given only very mild assumptions, the statistical interpretation of the quantum state is inconsistent with the predictions of quantum theory. This result holds even in the presence of small amounts of experimental noise, and is therefore amenable to experimental test using present or near-future technology. If the predictions of quantum theory are con rmed, such a test would show that distinct quantum states must correspond to physically distinct states of reality.
Nice read but what about entanglement though? In my textbook’s interpretation, when I measure a particle, of an entangled pair, the wavefunction of the other collapses too, as if I had measured it. I can’t control what it collapses to, but surely it must collapse? (To ensure the correlations seen in Bell like experiments I mean). I don’t see how decoherence theory and non-local Bayesian conditioning fit into this picture (where a wavefunction really collapsing makes the experiment much easier to understand).
In spite of my question/objection I really enjoyed the article, thanks!
“… the introduction of basic randomness into the equations of physics is philosophically unobjectionable …” Can quantum theory explain the vacuum catastrophe and the space roar? It is possible for an electron to tunnel through a potential barrier, but can such a paradoxical electron carry a kinetic energy that is arbitrarily large? Consider Wolfram’s Cosmological Principle: The maximum physical wavelength is the Planck length times the Fredkin-Wolfram constant.
http://en.wikipedia.org/wiki/A_New_Kind_of_Science
Is there a final verdict on quantum theory versus Wolfram’s “A New Kind of Science”?
I’m interested in the claim that the statistical interpretation of quantum theory is inconsistent with the quantum theory, but haven’t read that paper. If you’ll excuse my making a skeptical comment without reading it:
When I was taught QM and when I teach it, I learned/teach that the mathematical content of the theory is a set of “expectation values”. That is, all the theory defines is a set of probability amplitudes and Born’s rule tells us how to convert those complex numbers into a set of probabilities for measuring something in a certain experiment. My experimental colleagues compare these probabilistic predictions to repeated measurements. Sometimes the quantum predictions end up being “certain” with a great degree of accuracy, as for example when we predict the specific heat of some material. That’s a macroscopic property and we don’t really need to do repeated measurements to get it right, beyond eliminating experimental errors.
But the basic predictions of QM are probabilities, so I don’t understand how anything but a statistical interpretation of it is possible.
I have a certain amount of sympathy for the person who said I want to have the many worlds interpretation without the many worlds, but I would put it a little differently: the many worlds interpretation puts an unnecessary and in my view wrong philosophical framework over these questions by insisting that the wave function is a real thing. I claim it’s no more real than ANY probability distribution.
I think, at base, the problem is that the notion of reality that some writers like to cling to is a false one. It’s a concept that sits inside human brains, based on their experience with/construction by macroscopic objects, where everything definitely happens or doesn’t happen.
As Dyson said, there is no earthly reason for the underlying rules of the world to “make sense” to us, because we’re a very special kind of system in the world, which was conditioned to perform certain tasks related to survival. For me, reality is nothing but the set of results of experiments that some macroscopic object can perform at some time in the history of the universe.
Those are the only things that obey, or can be expected to obey, the rules of logic that our brains understand “intuitively” (sometimes with a lot of work). A physical theory is a mathematical algorithm, invented by humans, to make predictions about future events given some measurements of present events (there are quantum gravity issues about what past and future and time itself mean, but IMHO, these issues about the interpretation of QM can be discussed without getting into that). It has to satisfy rules that are not just opinions but things that anyone with enough mathematical sophistication can work through by themselves and come to the same conclusions as anyone else doing it. And it has to agree with experiment, with the maximum precision you can do the experiment.
That’s all it has to do.
I can see that I’m not going to be able to keep up with all the comments here and answer even those that are phrased politely. Let me just comment on this last one, about the entangled pair. QM makes a prediction like:
the state of the pair is (a | + – > + b |- +>) |N>. The meaning of this state is that there’s a probability amplitude for either particle to have spin up, but the spins are anti-correlated with probability one. The second factor in this wave function is the “ready to measure” state of the apparatus. It’s actually a huge collection of states, with N labeling just one average value like the position of a macroscopic needle. When I make a measurement, the wave function becomes
(a | + – > | N_+ > + b |+ – > | N_- > ) where |N_+ > is one of the many states with the needle UP and | N_- > one of the many states with the needle down. The microstates with the needle up or down don’t even have the same exact energies, and we’re certainly not in an energy eigenstate. The microstate is changing rapidly during the course of the experiment. I do the measurement locally at the position of particle 2 on the planet earth, and I’ve sent particle 1 to the (formerly known as) planet Pluto. The new wave function says “there’s probability |a|^2 for the needle to be up and |b|^2 for the needle to be down, and the interference between these two possibilities is so small that you couldn’t measure in a time so long that it doesn’t matter if I measure it in Planck times or ages of the universe”. That’s all it says. So, as with any probabilistic theory, you do the same thing many times and compare the frequencies to the predicted probabilities, and after doing that enough times you become convinced that the predictions are correct with some confidence level. Look at any paper on experimental physics. That’s how you’ll see the results quoted.
There’s nothing non-local here. You set up the correlation a long time ago, and waited for particle 1 to get to Pluto. That journey was carried out at a velocity less than or equal to the velocity of light. You assure me that you arranged the particles to be absolutely anti-correlated in spin when you sent them on their way and that nothing has intervened in the meantime to flip the spin of the particle I don’t have in my lab, relative to the one that I do. All of these assurances are implicit in the statement that “the state of the system before it interacts with the apparatus is thus and such”. So my conclusion that the spin on Pluto is up whenever I measure the spin on earth to be down, is not based on spooky action at a distance, but on things you’ve told me that you’ve done in (causally) setting up the experiment.
The old Copenhagen interpretation of quantum mechanics wasn’t just philosophically incomplete, but it was also physically incomplete: There was supposedly an ill-defined “Heisenberg cut” that divided classical systems from quantum systems, so the world was somehow described by two different frameworks without a well-defined line dividing them.
But nowadays, with density matrices and decoherence, there are no systems (maybe apart from questions in cosmology) that we cannot in principle treat quantum-mechanically. For macroscopic systems it becomes intractable, of course, but there are no more Heisenberg cuts. We can see why systems start behaving more classically as they get bigger.
So quantum mechanics, as written in terms of density matrices and decoherence, is at least physically complete, if not philosophically complete. That makes the problem of interpretation less exciting for many physicists.
But let’s probe the philosophical incompleteness question for a moment. In classical mechanics, one can say that a system described by a given probability distribution is actually occupying one of its possible states — we just don’t know which. But we can say the same thing for a quantum mechanical system if we insist: We can always say that it is secretly occupying the state labeled by one of its density-matrix eigenvectors. (And, apart from physically unachievable measure-zero scenarios, there are no true degeneracies in any density matrix, so its eigenbasis and thus its list of eigenvectors is unique.)
Sure, sometimes making this insistence permits superluminal changes in a particle’s state, as in certain experiments involving EPR pairs. But superluminality that doesn’t transmit observable information — and quantum mechanics elegantly satisfies this condition — does not violate causality or special relativity. There are lots of such phenomena already, from phase velocities to even the Higgs when it first goes tachyonic in the early universe before condensing to its present-day vacuum expectation value. Indeed, a beautiful way to understand the necessity of antiparticles (see Weinberg’s book on Gravitation) is that the Heisenberg uncertainty principle permits particles to jump occasionally outside their light cones — in an unpredictable and therefore information-empty way — which must then be seen by other Lorentz observers as antiparticles.
Also, sometimes it’s possible to imagine that some sufficiently big system — the whole universe? — remains always in a pure state, even though every human being inside has a nice, mixed density matrix. (That presumes that there is a well-defined, closed system that we can call the universe — still an open question.) But a person is not the universe, so we’re not speaking about the same system anymore. Taking seriously the ontological status of one of a system’s density-matrix eigenvectors requires letting go of the classical idea that systems and their sub- and supersystems must all be in definite states that same classically consistent with each other. But so what? I can still say that any given system is definitely in one state or another, our logical prejudices aside.
So realism is possible, as long as your definition of a state is something labeled by an eigenvector of a density matrix, and as long as you don’t care about superluminal effects that never transmit any actual information, information being defined according to the precise quantum Shannon entropy formula.
There’s a thorough discussion of these points in an earlier Cosmic Variance comments section — see http://blogs.discovermagazine.com/cosmicvariance/2010/12/12/interview-on-static-limit/ .
#6 “What Bell proved is that no local theory can reproduce the predictions of QM.”
Not quite, but this is a common misconception. What Bell (and successors) proved is that no local, realist theory is consistent with QM. That is, you either have to give up on locality or realism (or both). It’s a subtle, important, and often neglected distinction.
Bell himself said that DeBroglie-Bohm theory, which foresakes locality for the sake of realism, was consistent with his theorem and he didn’t understand why it didn’t get taken more seriously.
David Brown #13:
Is there a final verdict on quantum theory versus Wolfram’s “A New Kind of Science”?
I would say the verdict was already in long before ANKOS hit the printing presses! 😉
For more details, see a review of ANKOS that I wrote back in 2002. There I examine Wolfram’s “long-range thread” idea to account for the Bell inequality violations in classical cellular automata. I show that, even after we’ve given up on locality, the thread idea can’t be made compatible with Wolfram’s own requirements of determinism and relativistic invariance. (A similar argument would be made famous a few years later by John Conway and Simon Kochen, under the catchy name “The Free-Will Theorem.”)
Carl #16,
“What Bell (and successors) proved is that no local, realist theory is consistent with QM. That is, you either have to give up on locality or realism (or both).”
Not quite, but this is a common misconception. 😉
What Bell proved is that assuming that every possible measurement – even if not performed – would have yielded a single definite result, then no local, realist theory is consistent with QM.
This assumption is called contra-factual definiteness or CFD. What Bell really proved was that every quantum theory must either violate locality or CFD. The many-worlds theory, with its multiplicity of results in different worlds, violates CFD and thus is both local and “realistic”.
Tom, this is as good or better an explanation as I’ve read (as in, “damn, I wish I’d thought of that”).
Having said that, I do have a couple of nitpicks, and a question:
1) The Katrina analogy is a little misleading. If we think of the probability as a field, which I think is a very enlightening picture, it doesn’t actually collapse to zero in Galveston when we measure Katrina in New Orleans. In fact, the field has continuously evolved until the probability of it hitting Galveston became vanishingly small. When we measure Katrina and find it in New Orleans, the only thing that “collapsed” was our lack of knowledge; the probability field itself only ever evolved. I’m almost certain that this is what you meant, but it wasn’t entirely clear.
2) I think that the whole confusion about “collapse” and the “measurement problem” is a very unfortunate historical accident. In the earliest days of QM it’s clear that people were doing the best they could with adapting profoundly counterintuitive concepts to otherwise inexplicable experimental results. Two things were clear: very small, isolated systems obeyed QM; and macroscopic systems appeared classical. Given how hard it was to get quantitative predictions about even the simplest of systems correct, the question of what happened between microscopic and macroscopic could be set aside for another day. Unfortunately, somewhere along the way the concepts of “collapse” and “measurement” went from being placeholders for “we don’t know, we’ll get back to it when we have a better grasp of the fundamentals” to being dogma.
3) You talk about how overwhelmingly large the number of states is for a modestly sized macroscopic object. I think it would be useful (especially if you ever decided to expand this for a more general audience than the physics undergrad) to illustrate just how rapidly the number of states grows for even a handful of atoms. Even a system of just 100 atoms has 10^100 states. To put in non-technical terms, if we drew a graph of the number of states, the transition from “purely quantum” to “apparently classical” is so steep and rapid, it’s easy to see how it could be mistaken for instantaneous.
Finally, the question: is it possible to conceive of an experiment that would clearly distinguish between “decoherence” and “collapse”? Presumably this would start with a system that is purely quantum (say, a simple double slit) and then “measure” the outcome of that experiment not with an enormously macroscopic instrument such as a photographic film but instead with a microscopic system of, say, a few tens of atoms — small enough that the “instrument” still has measurably quantum behavior. This would definitively demonstrate that the ideas “instantaneous collapse” and a special role for observers or measurements are simply ill-conceived.
“I have a certain amount of sympathy for the person who said I want to have the many worlds interpretation without the many worlds” –tom banks.
That was Scott Aaronson in comment #10 but to me it looks much more like the relational interpretation:
http://en.wikipedia.org/wiki/Relational_quantum_mechanics
Michael #18: Yes, you are correct. I was being rather too casual with the use of the word “realistic”, in trying to emphasize that Bell does not require you to give up locality if you are willing to give up other things 🙁
On a different but related note, I’ve never understood the appeal of Many Worlds to a professional physicist. Surely it has all the problems of the Copenhagen interpretation (e.g. it replaces “instantaneous collapse” with “instantaneous splitting”, and you still have to define what a “measurement” is in order to say when the splitting of universes takes place) and then piles on top of it an infinity of undetectable universes. (I suspect its appeal to amateurs is because it sounds so science-fictiony and the philosophical implications are perfect fodder of late night undergraduate conversations…)
Carl #21,
Not an expert by any means, certainly an “amateur”, but a long ways away in years from being an undergraduate. 🙂
Nevertheless, it seems to me that that many-worlds predicts/retrodicts that wavefunctions appear to collapse when measurement- like interactions and processes occur via decoherence, but claims that the wavefunction does not actually collapse but continues to evolve according to the usual wave-equation. This, I believe, emerges naturally from the linearity of the wave-equation.
People have attempted to construct non-linear theories so that microscopic systems are approximately linear and obey the wave equation, while macroscopic systems are grossly non-linear and generate collapse. I think Scott Aaronson’s comment above addresses this issue from a more logical/philosophical perspective.
My understanding is that from a technical perspective all these efforts have made additional predictions which, when tested, have failed. Another reason for doubting that any collapse actually takes place is that the collapse would have to propagate instantaneously. Not fatal, but unpleasant and difficult to reconcile with special relativity and some conservation laws.
Reason enough, it seems to me, for professional physicists to at least take it seriously.
Carl #21:
Finally, the question: is it possible to conceive of an experiment that would clearly distinguish between “decoherence” and “collapse”?
Unfortunately, I think the only possible such experiments would involve
(1) taking some object that was previously considered to be a “conscious observer”—whether a human brain or (say) an artificially-intelligent computer, and then
(2) showing that the object can be placed in a coherent superposition, where the different branches correspond to perceiving different measurement outcomes.
If such an experiment were carried out, then any interpretation that insisted on collapse as an objective, physical process triggered by conscious observers would become untenable.
Needless to say, we seem impossibly far from any such experiment at the moment. (The Zeilinger group has done the double-slit experiment with buckyballs, but brains are another matter! 🙂 )
For any “smaller” experiment—such as the one you describe, involving a “measurement” performed by a few tens of atoms—a believer in objective collapse could simply say that the tens of atoms were nowhere close to “macroscopic” or “conscious,” and therefore no collapse was triggered. Such a believer would therefore make exactly the same predictions as the Many-Worlders, the Bohmians, and everybody else.
Scott Aronson #10
Your description of the situation is perfectly accurate, but both philosophers and physicists who have tried to make sense of it come to the same conclusion: there is, as you say, a double game going on with respect to the treatment of the wave function, and in the end the account is incoherent.
Here is Bell, in “Against ‘Measurement'”:
“Now, while quite uncomfortable with the concept of ‘all known observables’, I am fully convinced of the practical elusiveness, even the absence FAPP, of interference between macroscopically different states. So let us go along with KG [Kurt Gottfried] and see where this leads. “…If we take advantage of the indistinguishability of of rho and rho* [i.e. the exact density matrix after interaction and the density matrix without any interaction terms] to say that rho* is the state of the system subsequent to measurement, the intuitive interpretation of Cm as a probability amplitude emerges without further ado. This is because Cm enters rho* only via |Cm|*squared, and the latter quantity appears in rho* in precisely the same manner as probabilities do in classical statistical physics..”[This is a quote from Gottfried: the similarities to Banks are manifest. Bell continues…]
“I am quite puzzled by this. If one were not actually on the lookout for probabilities, I think the obvious interpretation of even rho* would be that the system is in a state in which the various Ψs somehow coexist:Ψ1Ψ1* and Ψ2Ψ2* and…[i.e. Bell notes the Many-Worlds character of this obvious interpretation. He continues….]
“This is not at all probability interpretation, in which the different terms are seen as not a coexisting but as alternatives: Ψ1Ψ1* or Ψ2Ψ2* or…
“The idea that the elimination of coherence, one way or another, implies the replacement of ‘and’ by ‘or’, is a very common one among solvers of the ‘measurement problem’. It has always puzzled me.”
Bell goes on to discuss how inadequate this approach is…everyone should read this piece.
As you (Scott) say, quite correctly, if one wants to regard the collapse as merely Bayesian conditionalization, there there has to be some fact that is being conditionalized on (e.g. the cat being either alive or dead), and that physical fact ought to be represented in the physics. If one regards the wavefunction as complete, there is no such fact. So one way forward is to reject the completeness of the wavefunction, as EPR suggested. But then one has to say what the physics is postulating.
Banks’s discussion of non-locality in #16 above shows exactly this confusion. He seems to think that it is trivial: the spins of the two particles were created to be anti-correlated on earth, and all you do when you find the result on Pluto is conditionalize on a pre-existing fact: just like Bertlmann’s socks. But we all know (and most clearly from GHZ) that this cannot be what is going on in QM. This double-thinking it-is-but-it-isn’t-Many-Worlds creates a fog of confusion that obscures Bell’s sharp result.
Carl #16
No, Bell nowhere assumes anything that can be called “realism” in his proof. The result is a mathematical theorem. If you think that the theorem employs a postulate that should be called “realism”, please identify it and justify the name. Bell shows that no local theory can reproduce the predictions of standard QM. He takes those predictions to include the claim that experiments have unique results, so there is a fact about what the correlations among results of distant experiments are. One can say that Many Worlds rejects this claim, but that of course lands us in a host of interpretive problems.