When physicists are asked about “parallel worlds” or ideas along those lines, they have to be careful to distinguish among different interpretations of that idea. There is the “multiverse” of inflationary cosmology, the “many worlds” or “branches of the wave function” of quantum mechanics, and “parallel branes” of string theory. Increasingly, however, people are wondering whether the first two concepts might actually represent the same underlying idea. (I think the branes are still a truly distinct notion.)
At first blush it seems crazy — or at least that was my own initial reaction. When cosmologists talk about “the multiverse,” it’s a slightly poetic term. We really just mean different regions of spacetime, far away so that we can’t observe them, but nevertheless still part of what one might reasonably want to call “the universe.” In inflationary cosmology, however, these different regions can be relatively self-contained — “pocket universes,” as Alan Guth calls them. When you combine this with string theory, the emergent local laws of physics in the different pocket universes can be very different; they can have different particles, different forces, even different numbers of dimensions. So there is a good reason to think about them as separate universes, even if they’re all part of the same underlying spacetime.
The situation in quantum mechanics is superficially entirely different. Think of Schrödinger’s Cat. Quantum mechanics describes reality in terms of wave functions, which assign numbers (amplitudes) to all the various possibilities of what we can see when we make an observation. The cat is neither alive nor dead; it is in a superposition of alive + dead. At least, until we observe it. In the simplistic Copenhagen interpretation, at the moment of observation the wave function “collapses” onto one actual possibility. We see either an alive cat or a dead cat; the other possibility has simply ceased to exist. In the Many Worlds or Everett interpretation, both possibilities continue to exist, but “we” (the macroscopic observers) are split into two, one that observes a live cat and one that observes a dead one. There are now two of us, both equally real, never to come back into contact.
These two ideas sound utterly different. In the cosmological multiverse, the other universes are simply far away; in quantum mechanics, they’re right here, but in different possibility spaces (i.e. different parts of Hilbert space, if you want to get technical). But some physicists have been musing for a while that they might actually be the same, and now there are a couple of new papers by brave thinkers from the Bay Area that make this idea explicit.
Physical Theories, Eternal Inflation, and Quantum Universe, Yasunori Nomura
The Multiverse Interpretation of Quantum Mechanics, Raphael Bousso and Leonard Susskind
Related ideas have been discussed recently under the rubric of “how to do quantum mechanics in an infinitely big universe”; see papers by Don Page and another by Anthony Aguirre, David Layzer, and Max Tegmark. But these two new ones go explicitly for the “multiverse = many-worlds” theme.
After reading these papers I’ve gone from a confused skeptic to a tentative believer. This happened for a very common reason: I realized that these ideas fit very well with other ideas I’ve been thinking about myself! So I’m going to try to explain a bit about what is going on. However, for better or for worse, my interpretation of these papers is strongly colored by my own ideas. So I’m going to explain what I think has a chance of being true; I believe it’s pretty close to what is being proposed in these papers, but don’t hold the authors responsible for anything silly that I end up saying.
There are two ideas that fit together to make this crazy-sounding proposal into something sensible. The first is quantum vacuum decay.
When particle physicists say “vacuum,” they don’t mean “empty space,” they mean “a state of a theory that has the lowest energy of all similar-looking states.” So let’s say you have some scalar field filling the universe that can take on different values, and each different value has a different potential energy associated with it. In the course of normal evolution the field wants to settle down to a minimum of its potential energy — that’s a “vacuum.” But there can be the “true vacuum,” where the energy is really the lowest, and all sorts of “false vacua,” where you’re in a local minimum but not really a global minimum.
The fate of the false vacuum was worked out in a series of famous papers by Sidney Coleman and collaborators in the 1970’s. Short version of the story: fields are subject to quantum fluctuations. So the scalar field doesn’t just sit there in its vacuum state; if you observe it, you might find it straying away a little bit. Eventually it strays so far that it climbs right over the barrier in the direction of the true vacuum. That doesn’t happen everywhere in space all at once; it just happens in one tiny region — a “bubble.” But once it happens, the field really wants to be in the true vacuum rather than the false one — it’s energetically favorable. So the bubble grows. Other bubbles form elsewhere and also grow. Eventually all the bubbles crash into each other, and you successfully complete a transition from the false vacuum to the true one. (Unless the universe expands so fast that the bubbles never reach each other.) It’s really a lot like water turning to steam through the formation of bubbles.
This is how everyone talks about the fate of the false vacuum, but it’s not what really happens. Quantum fields don’t really “fluctuate”; that’s poetic language, employed to help us connect to our classical intuition. What fluctuates are our observations — we can look at the same field multiple times and measure different values.
Likewise, when we say “a bubble forms and grows,” that’s not exactly right. What really happens is that there is a quantum amplitude for a bubble to exist, and that amplitude grows with time. When we look at the field, we see a bubble or we don’t, just like when we open Schrödinger’s box we see either a live cat or a dead cat. But really there is a quantum wave function that describes all the possibilities at once.
Keep that in mind, and now let’s introduce the second key ingredient: horizon complementarity.
The idea of horizon complementarity is a generalization of the idea of black hole complementarity, which in turn is a play on the idea of quantum complementarity. (Confused yet?) Complementarity was introduced by Niels Bohr, as a way of basically saying “you can think of an electron as a particle, or as a wave, but not as both at the same time.” That is, there are different but equally valid ways of describing something, but ways that you can’t invoke simultaneously.
For black holes, complementarity was taken to roughly mean “you can talk about what’s going on inside the black hole, or outside, but not both at the same time.” It is a way of escaping the paradox of information loss as black holes evaporate. You throw a book into a black hole, and if information is not lost you should (in principle!) be able to reconstruct what was in the book by collecting all of the Hawking radiation into which the black hole evaporates. That sounds plausible even if you don’t know exactly the mechanism by which happens. The problem is, you can draw a “slice” through spacetime that contains both the infalling book and the outgoing radiation! So where is the information really? (It’s not in both places at once — that’s forbidden by the no-cloning theorem.)
Susskind, Thorlacius, and Uglum, as well as Gerard ‘t Hooft, suggested complementarity as the solution: you can either talk about the book falling into the singularity inside the black hole, or you can talk about the Hawking radiation outside, but you can’t talk about both at once. It seems like a bit of wishful thinking to save physics from the unpalatable prospect of information being lost as black holes evaporate, but as theorists thought more and more about how black holes work, evidence accumulated that something like complementarity is really true. (See for example.)
According to black hole complementarity, someone outside the black hole shouldn’t think about what’s inside; more specifically, everything that is happening inside can be “encoded” as information on the event horizon itself. This idea works very well with holography, and the fact that the entropy of the black hole is proportional to the area of the horizon rather than the volume of what’s inside. Basically you are replacing “inside the black hole” with “information living on the horizon.” (Or really the “stretched horizon,” just outside the real horizon. This connects with the membrane paradigm for black hole physics, but this blog post is already way too long as it is.)
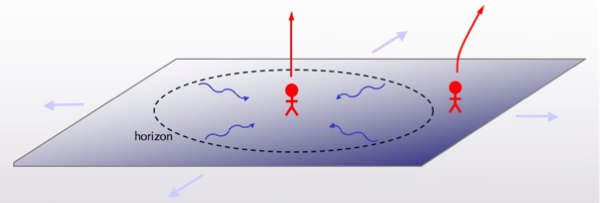
Event horizons aren’t the only kind of horizons in general relativity; there are also horizons in cosmology. The difference is that we can stand outside the black hole, while we are inside the universe. So the cosmological horizon is a sphere that surrounds us; it’s the point past which things are so far away that light signals from them don’t have time to reach us.
So then we have horizon complementarity: you can talk about what’s inside your cosmological horizon, but not what’s outside. Rather, everything that you think might be going on outside can be encoded in the form of information on the horizon itself, just like for black holes! This becomes a fairly sharp and believable statement in empty space with a cosmological constant (de Sitter space), where there is even an exact analogue of Hawking radiation. But horizon complementarity says that it’s true more generally.
So, all those pocket universes that cosmologists talk about? Nonsense, say the complementarians. Or at least, you shouldn’t take them literally; all you should ever talk about at once is what happens inside (and on) your own horizon. That’s a finite amount of stuff, not an infinitely big multiverse. As you might imagine, this perspective has very deep consequences for cosmological predictions, and the debate about how to make it all fit together is raging within the community. (I’m helping to organize a big meeting about it this summer at Perimeter.)
Okay, now let’s put the two ideas together: horizon complementarity (“only think about what’s inside your observable universe”) and quantum vacuum decay (“at any point in space you are in a quantum superposition of different vacuum states”).
The result is: multiverse-in-a-box. Or at least, multiverse-in-an-horizon. On the one hand, complementarity says that we shouldn’t think about what’s outside our observable universe; every question that it is sensible to ask can be answered in terms of what’s happening inside a single horizon. On the other, quantum mechanics says that a complete description of what’s actually inside our observable universe includes an amplitude for being in various possible states. So we’ve replaced the cosmological multiverse, where different states are located in widely separated regions of spacetime, with a localized multiverse, where the different states are all right here, just in different branches of the wave function.
That’s a lot to swallow, but hopefully the basics are clear. So: is it true? And if so, what can we do with it?
Obviously we don’t yet know the answer to either question, but it’s exciting to think about. I’m kind of inclined to think that it has a good chance of actually being true. And if so, of course what I’d like to do is to ask what the consequences are for cosmological initial conditions and the arrow of time. I certainly don’t think this perspective provides an easy answer to those questions, but it might offer a relatively stable platform from which definite answers could be developed. It’s a very big universe, we should expect that understanding it will be a grand challenge.
In your article you said that one can draw a slice in spacetime that contains both the infalling book and the outgoing radiation. But can this slice of spacetime be really seen as slice of simultaneity? What if it in fact cannot?
I think there is still a difference: the many-uninverses together with the horizon complementarity implies that everything outside the horizon can be described by the Hilbert space of our universe, more specifically, its state now becomes a superposition of our universal states.
Whereas in multiverse, the total Hilbert space is the tensor product of the individual universal Hilbert spaces. The dimension difference is HUGE.
The picture is getting elegant and natural once we recognize that it is not universe splits apart (it’s always in superposition state) but observer is constantly branching. Our memory perceives a single path from root to current node. In fact the time from this point of view is not one dimensional – it seems one-dimensional only thanks to our perception.
Are we not a “causal patch” that promotes decoherence for another, or perhaps every other, “causal patch”?
It still seems to be a bit of a subjective perspective.
Brian Green’s book title ‘The Hidden Reality’ gets at the ontological or metaphorical aspect of many worlds (or call them many multiverses – that might yoke the two concepts together). But Green does not go far enough: the ‘reality’ of many worlds is not hidden in the way dark energy or the Higgs boson may be; it is a way of doing thought experiments about simultaneity and the nature of existence, old philosophical chestnuts that many physicists balk at. It doesn’t matter whether the many worlds are near or far, they exist as determinable realities that can exist simultaneously, not least for measurement purposes. The cosmological approach needs to go a little softer on the hard science and look at the issue as a conceptual one that has very little to do with boundaries or horizons, or even (meta)physical spaces. The problem started as a thought experiment that went wrong for Bohr and Heisenberg – Everett simply proposed a way of rethinking reality that is almost pre-Socratic in its elegance.
In one sense the MW of QM and the Multiverse of Susskind et al can’t be the “same”, since in the former the worlds affect each other through interference, while in the later, if I understand correctly, the various universes are separated and non-interacting.
What I found intriguing about both the Susskind and Nomura papers was the bit about deriving probability from the physical theories themselves, and that the MWI is not the problem, rather it is the solution. I just found it ironic that while critics point to the probability measure in MWI as being a “problem”, these papers point to the MWI as the “solution” to assigning probabilities over their multiverse schemes.
David George, do you have a website or blog? Can you post a link here? I would like to follow your comments on issues like these. You clearly have an intelligent approach.
Pingback: Tarinbot! / cuándo los multiversos interactúan. – Taringa!
Pingback: Why do we see our world as we do | Sarah's Research Blog
#82 doloop –I have no website (due to illiteracy, inertia, and funds). This is the only place I usually will comment. However I am willing to contribute the equations and explanations I have discovered during the last few years if there is somewhere to send them. Things keep changing but since I started reading “Big Bang science” (would that be creation “science”, or non-creation “science”?) in the 1990’s I have doubted the orthodox version. About the first “thought experiment” I did (before I even heard of a thought experiment) was to play God. If I were God, and I had one command, given what we know about the universe, what could it be? The answer is, “Expand!”. The result of this command is the universe we experience with our senses. The immediate consequence of this simple initial condition is a finite rate of expansion. We must assume God has an infinite bank of “energy” (unlike the Big Bang, where the window closes and it is all downhill from there). Now, from this infinite bank of energy God (or Zeus) pulls whatever amount Mother Nature (or Mrs. Zeus) wants. However, time intervenes. There may be an infinite amount of energy available, but there is not an infinite speed of time (i.e. infinite speed of light). The energy can be doled out only at a specified rate. The rate can be designated as c. This imposes a limit on the profligate Mrs. Zeus, who (naturally) wants more of everything, all at once, now! The expansion rate c defines both a rate of expansion of the universal ball of space, and the movement of disturbances through it. And the expansion rate has other consequences.
The amount of energy/space created per constant time unit of expansion continually grows by the cube of the radius (times 4/3 pi). This is like an acceleration upon an acceleration. This to me gives a truer picture of God as an infinite creative power than the other infinitudes I have seen (“Finite but unbounded? Infinite but bounded?” etc.).
Here the first consequence of expansion emerges. The only region of space where the field (the real, universal, whole, physical, energetic spatial field) expands (according to its initial condition or command) at its full potential (c) is at its outer surface. Everywhere within the field, space cannot expand at its full potential (because the space it would expand into is already occupied by itself). The easiest way to visualize this is to imagine a sphere expanding from a point (a tiny but finite point). After one second the outer shell of the sphere will have expanded at the distance covered by light in one second. In a region halfway from the shell of the sphere to the center point, (i.e. half the radius), the expansion is only half the distance covered by light in one second. So in this region there is an unused potential for motion equal to the amount of motion that is used. So expansion creates some “pressure of space” virtually everywhere throughout the universe. And on average, everywhere, no matter that the universe is expanding at its full potential at its limit, there is a constant pressure of unused space equal to the amount of space that exists. (That is, there is always twice as much energy in the universe as we think there is, which explains the failure of classical equations for magnetic moment.)
The universe responds to the pressure by rotating. I believe the matter particles form as bubbles in larger rotational motions (galactic dark matter size and maybe larger). Inside each bubble is a region of space trying to get out; outside each bubble is the universe trying to get in. And so on. I believe the initial bubbles are neutrons. The field can hold a neutron bubble together for about 15 minutes before it separates into two bubbles (with an intermediate field — I said there is no force between electron and proton, but it can be modelled as exchange of a magnetic flux quantum.)
This “creation scenario” gives the natural result that an electron (and protonA) can be modelled as a rotating sphere, because its charge is spread out over one second, etc. You then can get frequency, circumference, and from Planck and Einstein you get h and q. And with f (frequency of rotation, not of oscillation), h and q you will find v (Volts, or the equivalent of eV). You then have two massless current spheres. There are I believe significant coincidences: V(e) x V(p) = approx. 2 q / h (Josephson constant); and f(e) / v(p)^2 = 140.35 (approx. inverse of fine structure constant). By designating the exact values, you come up with a system proton-electron ratio that is 1860.308707, not the approx. 1836 of the conventional model. That is, in their system state the proton and electron have different masses than in their free state. And there is much more to be found out from there.
This “model” can be attached to the conventional models by conversion factors — which themselves involve the spin-g factor! There is something here that has not been discovered by anyone except me — it is a mystery to me because I am not a scientist and don’t know the terminology (apart from the general ideas). I think it only came about because I am not a scientist and didn’t know what I was doing. But each step along the way it seemed to come clearer — the end (for the scientists) being a world of research into triaxial motions of space!
As I said, I have more equations, but I think anyone can get them given the information here. And then a different world opens up. I have done only the electron and proton, also the Ballmer series, etc. for spectral emission/absorption lines. Someone other than me will end up doing something like this sometime because the current models are so far out it isn’t funny. So eventually someone would have to do it. I have written (to myself, as it turns out) many words on this subject (it comes down to EPR), I am tired of rewriting. In general I think the answer is to go back to the 1920’s where Einstein tried to figure out a hidden variable equation and couldn’t, Bohr’s model didn’t work, the probability amplitude for locating a material point worked, and a spatially extended model wasn’t needed. But from there you can trace how point particles in fields have bedevilled physics. Einstein said not to put particles in your fields, and he was right. Quantum mechanics is not a complete description of the physical reality of electrons, protons, light, etc. It is far past the time to consider a realistic model.
82 doloop,
Well, you asked for it 😉
Pingback: De la rencontre de l'univers multiple et des multiples univers | Ze Rhubarbe Blog
I don’t understand how the many worlds interpretation can possibly be true. Actually, I think it’s nonsense. When I open the box and find a dead cat, why am I living in the universe harboring a dead cat and not one that’s alive? What governs which universe I am aware of? You see my point? MWI is pure nonsense. The universe doesn’t magically split whenever an “observation” is made.
I’ve read (arxiv.org/abs/1105.3796), and have a few comments. First, there are only 2 possible alternatives that I can see that agree with all aspects of reality. First, that time and space are lineal, but causality works both from past to future and future to past, and where decoherence is entirely reversible (that is, nothing ever really happens, kind of like existence from the point of view of a photon, where creation and annihlation occurs at the same time) over time. This would solve quantum entanglement action at a distance. The second would be a multiverse as described with the following caveats: 1) there must be a probabillity axis with a dimensional magnitud between 1 and 0, describing parallel universes with all possible probabillity states. 2) the intersection point between the probabillity axis and time-space, can only have two “real” states: interaction and non-interaction. 3) all intersection points in time-space for the same particle, are the same intersection point in the probability axis.
does time stay time in other universes and if a paraell universe colaspes what happens to the time in the universe beside it and if one runs backwards and the other forwords what happens
can anyone anwser my question
here’s my answer ed…
Everything is now and You are here!!!
That only leaves one other option if it were not true. You are not here and everything is not now, meaning you are dead !
http://pollywannacracka.blogspot.com/2007/06/predetermining-collapse.htm
Pingback: Many worlds theory, many interpretations? | Uncommon Descent
Pingback: Assorted links — Marginal Revolution
Per MWI: the universe in state A (call it #A) can ‘split’ into #B and #C; could #C (say) ‘join’ with #D to make #F? If not we have (at last!) a truly unidirectional temporal process; if not, then information is lost, and quantum determinism (so dear to the heart of Leonard Susskind) fails. And yes, the two- multiverse and MWI- could be the same idea, because we couldn’t possibly know enough at this point to say otherwise.