I’ve been meaning to post about the claim that experimenters have demonstrated that the proton/electron mass ratio is changing with time. Although it’s a fascinating discovery if true, there’s something that doesn’t quite smell right about it. So I hit on the idea of first posting about the idea of physics claims not “smelling” right more generally. But then I thought that such a post would necessarily involve a careful exposition of one particular example. So it’s time for the story of the Screwy Universe.
In April 1997, while a postdoc at the Institute for Theoretical Physics at UC Santa Barbara, I received an email from George Field, who had been my Ph.D. advisor. He was suggesting that I take a look at a news article that had appeared on the front page of the New York Times. George is one of my favorite people in the whole world, and I owe whatever success I may have had as a scientist to his insightful guidance in my early career. But okay, I was busy, and didn’t immediately look at the article — lots of crazy stuff appears in the NYT, after all.
But George wrote again, gently suggesting that I really should take a look at this article, which I finally did. And it was indeed striking. Two scientists, Borge Nodland of the University of Rochester and John Ralston of the University of Kansas, were claiming that they had detected a violation of a fundamental principle of modern cosmology — isotropy, the idea that space looks the same in every direction. In particular, they had considered the polarization of radio waves coming from distant quasars, and looked for a rotation of the polarization angle as the waves traveled through space. And they had found evidence of just such a rotation! If N&R were right, there was a preferred direction in the cosmos — along that direction, polarized radio waves would gently corkscrew as they traveled through space, while in the opposite direction they would twist the other way. Completely contrary, of course, to our conventional expectations, which are that (1) polarized waves maintain their polarization angles in empty space, rather than rotating, and (2) every direction in the sky is basically equivalent to every other direction.
Clearly important stuff. But for George and me this hit particularly close to home, as we had previously collaborated with particle theorist Roman Jackiw on a very similar-sounding project, looking for gentle rotations in the polarization of distant sources (and not finding any). In fact, this work with George and Roman was the topic of my first published paper. Our motivation was to test Lorentz invariance by searching for the effects of a constant vector field spread throughout spacetime. It turns out that such a vector can couple to ordinary electromagnetism, but only in certain specified ways. We showed that, if the vector pointed mostly in the time direction of spacetime, its effect would be to uniformly rotate the observed polarization of distant radio sources; we then searched for such an effect in the existing data, and didn’t find any. My job as the beginning graduate student was to look in the literature for measurements of the polarization angles and redshifts of as many galaxies as I could find. I managed to scrape up 160 such galaxies, which was enough to put a good limit on the effect we were looking for. (I should say that, as a nervous beginning graduate student, George was extremely intimidating because of his formidable intellect and amazing accomplishments, but in other circumstances one would recognize that he was extremely gentle and easygoing. Roman, on the other hand, was intimidating, period. But also fantastically smart, and an excellent collaborator once one calmed down and got into the science.)
At the time, anxious young ingenue that I was, I was somewhat worried that writing my first paper on a topic as outlandish as Lorentz violation might spell the premature end of my career. Nowadays, of course, it is all the rage, and we are proud pioneers.
So the news of Nodand and Ralston’s work had a personal resonance — it sounded like they were investigating something similar. And then I noticed in the NYT story — 160 radio galaxies! These guys were using the very data I had typed in as a first-year grad student. (Although, as it later turned out, they were careful enough to check everything, and had found a few typos.) In fact they had basically done exactly the same thing that we had done, except that they had considered a Lorentz-violating vector field that was pointing in a spatial direction instead of in the time direction. As a result, they were asking whether there was a direction-dependent rotation of polarizations — clockwise if you looked at one side of the sky, counter-clockwise if you looked at the other — rather than a uniform one across the sky. And, remarkably, they seemed to be saying that there was such a rotation!
But I didn’t believe it, not for a second. True, we hadn’t carefully placed a limit on such an effect, but I was convinced that I would have noticed it in the course of playing around with the data. Not to mention, there was no good theoretical reason to suspect that such an effect might exist. In short, it didn’t smell right.
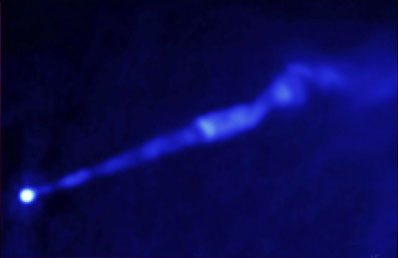
As it turns out, Nodland and Ralston had simply made a mistake. What they, and before them we, were doing was comparing the polarization from distant quasars to their orientation angles on the sky. Many of these quasars have extended jets coming from massive black holes at their centers, and the orientation of these jets defines (more or less) an orientation on the sky, as in the image of M87 above from the Very Large Array. We expect that there will be magnetic fields that stretch along the jet, and that free electrons will be spinning in circles perpendicular to the magnetic fields. These electrons then emit synchrotron radiation — the motion of the electrons produces a time-dependent electric field, which travels to us as radio waves. Because that motion is perpendicular to the background magnetic field (and thus to the jet), the electric field in the resulting radio waves is likewise perpendicular to the jet, and its that electric field that defines the polarization. In other words, on physical grounds we anticipate that the quasar polarization is at roughly 90 degrees to the angle of the jet on the sky. We were looking for any systematic deviations from this relationship, either in the same sense everywhere (George, Roman and I) or clockwise in one direction and counterclockwise in the other (Nodland and Ralston).
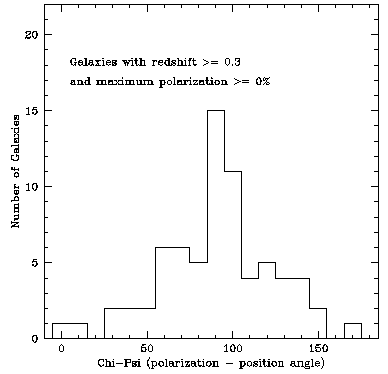
You’ll notice, though, that neither the polarization angle nor the orientation angle of the jet is uniquely defined; rotating by 180 degrees gives you an equally good answer. So the difference between them is likewise subject to a 180-degree ambiguity. Since you expect the difference to be 90 degrees, this doesn’t make much of a difference in practice; indeed, if you resolve the ambiguity by defining the difference to lie between 0 and 180 degrees, there is an obvious peak at 90.
However, Nodland and Ralston were working under the assumption that the difference should naturally be zero degrees, rather than 90. That is, they assumed that the polarization and orientation should naturally be parallel. To resolve the 180-degree ambiguity, they defined the difference between the polarization and orientation angles to be between 0 and 180 degrees if the quasar was in one hemisphere of the sky, and between -180 degrees and zero if it was in the opposite hemisphere. This was a bad thing to do, especially when combined with what they did next, which was to then plot the data as a function of redshift and fit it to a straight line. In other words, they made a plot in which all of the points would lie in the bottom left and top right quadrants by hypothesis, and then asked if the best-fit line would have a nonzero slope (which would purportedly indicate that the polarization had been rotating as it traveled through space). Of course, it had to, by construction.
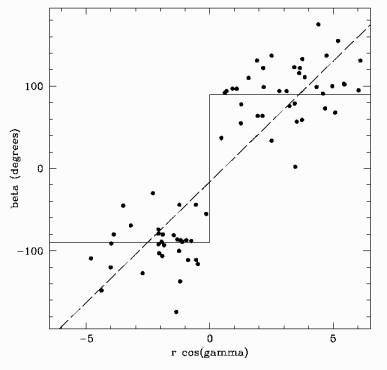
Here are the data, with the diagonal N&R fit. The piecewise-constant line, just indicating that the data are clustered at plus or minus 90 degrees, is statistically a much better fit. Indeed, if N&R had been correct, the prominent peak at 90 degrees in the above histogram would had to have been a complete accident, representing a bunch of points really centered around zero that had fortuitously been rotated to plus or minus 90. Much easier to believe that the polarization is perpendicular to the jets, as it should be, and that there is no fundamental anisotropy or preferred direction in the universe.
Of course, appearing on the front page of the NYT, the N&R paper sparked a great deal of interest and follow-up papers, as detailed here (with many by-now-broken links). Even an appearance in the funny pages! George and I wrote a quick response paper, one of several that appeared. It was the only time in my life when I worked feverishly over the course of a couple of days to write a paper from scratch — not normally my favored mode of operation.
But the good news is that the dust-up put this anisotropy stuff back in my mind, and a year later I realized that you could get exactly this kind of effect — a rotation of polarized photons as they traveled from distant quasars to us — from quintessence, a dynamical field that could be the dark energy. An evolving scalar field naturally violates Lorentz invariance by picking out a preferred direction in spacetime — in this case, the direction in which the field is evolving (presumably the timelike one). Models of quintessence that feature symmetries to protect them from being ruled out tend to allow for only one kind of interaction with ordinary matter, which is exactly the kind that can push around the polarization states of photons. Interestingly, the current quasar data are not quite good enough to test this prediction at sufficient precision that we should have seen the effect if it is really there. So there is one way to win the Nobel Prize lurking out there — directly detect the existence of quintessence by discovering a systematic redshift-dependent rotation of polarized light from distant galaxies. You only have to improve the existing limits by one or two orders of magnitude. So what are you waiting for?
Cool stuff! Does polarization by interstellar dust in the Milky Way affect these measurements at all?
What do I look like, an astronomer? My impression is, yes you have to worry about it, but it’s not that hard to take it into account when measuring the intrinsic polarization. In particular, Faraday rotation is wavelength-dependent and can be corrected for; the effects we were looking for were wavelength-independent.
So, now, what about varying m_p/m_e?
When Lubos had a post about I already asked the following question (without getting a goot answer): We know that m_p is basically Lambda_QCD, the scale at which alpha_s the strong coupling has unit strength, so a natural interpreation would be that what varies is, at least to some part, alpha_s.
Now, if you believe in GUTs, the three different alphas are not independent. Now that we have varying alpha_s as well as varying fine structure constant (according to Webb etal), how does this translate to a variation of the meeting point (Lambda_GUT, alpha_GUT). For a generic variation (one that does not happen to be in the direction of the running of either alpha_s or alpha), one would expect that the two variations are somewhat similar in size. Is this the case and are the two variations thus compatible? Too bad it’s so hard to observe the Fermi constant at cosmological distances….
Dear Robert,
why don’t you also allow “m_e” to vary as well as an explanation of the hypothetical variation of the mass ratio? Besides LambdaQCD or alpha_{string}, you can change the electron’s Yukawa coupling, the quark Yukawa couplings, the Higgs vev – that primarily affects the electron mass, not the proton mass – or any other constant for that matter.
When you only vary one of the three Standard Model couplings, you may be sure that the gauge coupling unification will disappear. If you only care about the intersection of two lines, then the meeting point (energy scale near the GUT scale) will of course depend extremely sensitively on the low-energy values of the couplings – because it’s the log (scale) that enters a linear formula and the lines are almost horizontal.
If you vary two out of three couplings, you are right that you can preserve unification. You have two pieces of information here. However, they are not about two fundamental gauge couplings. The fine structure constant depends both on the U(1)_Y and SU(2) couplings. The mass ratio depends on very many things. I understand your picture – to check whether these two variations preserve the unification in the past – but I am afraid that we don’t know enough to calculate this consistency check, especially because the mass ratio is affected by Higgs vev and the Yukawa couplings that can also depend on time.
But it’s your idea and it could be interesting. Just do the calculation. Assume that the mass ratio only comes from varying the QCD coupling. Calculate what the couplings were X billion years ago, and try to calculate all three couplings at that time and reverify whether the unification is preserved. Such an agreement would be a tantalizing circumstantial evidence of the time-dependence. Unfortunately, as you have probably noticed, you would also need a third information about a third coupling in the past – such as the evolution of the Fermi constant. I doubt this can be calculated. Beta decay in the cosmological past is hard to observe, is not it?
Best
Lubos
I HAVE done the calculation (hep-ph/0305026), including different possible scenarios for the variations of the Higgs vev, superpartner masses, Yukawa couplings, etc. etc. etc. in unified theories.
This has been discussed since 2001. Calmet & Fritzsch, Langacker, Segre and Strassler, and Dine, Nir, Raz and Volansky have also put forward scenarios.
While there is no unique ‘prediction of unification’, you do get a prediction when plain unification is supplemented by bells and whistles that tell you where the Higgs vev., electron mass etc. come from, in terms of a unified coupling. Model-building muck in other words.
(Variation of the unification scale is meaningless unless you also consider gravity and define the Planck mass.)
Despite this model-dependence, the generic result for 4d unified theories, which is rather easy to understand from dimensional transmutation, is that the fractional variation of m_p/m_e is one or two orders of magnitude larger than that of alpha. So if the variations are real and of the *same* order, it becomes quite difficult to maintain unification unless there is some sort of cancellation.
A check on many different parameters including the weak interaction in the cosmological past is primordial nucleosynthesis. Yes, it is not very clean and has all sorts of degeneracies, but it has a very large lever arm in time and redshift! Your reference here is a paper last year by Chamoun et al.
To return to the original subject of the post, while the Nodland & Ralston story is a nice one, I strongly doubt it has anything to do with the current question of m_p/m_e – or the ‘varying alpha’ business, which is still under debate. The implication seems to be that the experimenters and astronomers may have made a simple and dumb mistake which caused an artificial signal to appear in their results. But the methods used in their investigations have been developed over a number of years and been heavily scrutinized, and the statistics used are immune against most forms of dumb mistakes. To be more precise, while errors in each individual measurement exist, no-one has yet found any good reason why they should not average to zero if the spectra of far-distant atoms and molecules really are the same as here in the lab, up to the effect of redshift.
That’s all people are doing – seeing if the null hypothesis stands up.
We should know more in a few years. Hindsight is a wonderful thing!
Thomas
Thanks, Thomas for this explanation. So what are the numbers that have been observed, do they fit your pattern?
One thing one should not forget of course is at what time the values are observed (or redshift if you like). From what I picked up, for the fine structure constant, a constant rate of change is not consistent if one takes Webb etal and Okla data into account. So, is the m_p/m_e variation happening at a similar redshift as fine structure constant variation?
Wouldn’t a variation of Fermi’s constant have an observable impact on distant supernovae?
The best limits on the variations of most constants over cosmological timescales comes from Big Bang nucleosynthesis. It’s very long ago (redshift of one billion, or when the universe was three minutes old), but the precision isn’t great. If the Fermi constant (i.e., the Higgs expectation value) were to be different during BBN, it would change the neutron/proton mass difference, and thus both the neutron lifetime and the equilibrium n/p ratio, as well as the nuclear binding energies. You typically find that G_F and other constants must be within about 10% of their current values. See for example:
http://arxiv.org/abs/astro-ph/0508378
>Although it’s a fascinating discovery if true, there’s something that doesn’t
>quite smell right about it. So I hit on the idea of first posting about the idea of
>physics claims not “smelling” right more generally.
Aaah, the sweet smell of ‘rightness’. Like pornography, we can’t define it but we know it when we …errr… see it.
An undergrad advisor of mine Tom Devlin , first pointed out such an effect to me, but maintained that it wasn’t a smell, but a sound. He called it the “‘ring’ of rightness.” Here, we know it when we hear it.
It’s probably also what we call physics intuition, and it really is amazing what a powerful force it can be. Frequently I think I’m right about something only to be later proved wrong, but when that ‘ding’ goes off after a thought that first glimpse usually turn out to be correct in the end.
Hi Sean.
In my first publication, me, Horace Stoica and my supervisor Guy Moore put some bounds on a class of spontaneous Lorentz violating vector-tensor theories that provide a cherenkov-type mechanism by which cosmic rays could cool off way too much on even galactic distance scales.
I think we assumed throughout that the vev of the vector field was time-like and I recall having some very good reason for doing so. Barring acausal dispersion relations (in the less than speed of light sense), we found that these theories were very tightly constrained.
I came away from that work distinctly sceptical of any Lorentz violating theories, since my impression was that the spontaneously broken models were really the only viable candidates. I’ve been told in rather passionate prose that this is too short sighted, but no-one can really tell me why. Any help?
Thanks.
Just for the record: How did the positive cosmological constant smell when it was first seen in supernova data and what about neutrino oscillations?
Robert — the cosmological constant was a surprise, but it smelled very right. There were two competing groups, both highly competent, looking for precisely that effect, and the result solved several well-known problems at once. Likewise, neutrino oscillations were something that many people suspected for years.
Joshua — I think I also agree that only spontaneously-broken models of Lorentz violation make sense, but there are plenty of such models. Unless I am misunderstanding what you mean.
Dear Sean,
Your reminiscences in your blog about the Screwy Universe brought back
some memories. I had been back in India after a PhD from
Wisconsin and I had been floundering about for some new
ideas (and a permanent job!) when I read your paper with
Field and Jackiw. It led me (with a couple of graduate students) to write a paper on getting
such a Chern-Simon type of term from one loop effects in QED with CP violation.
We got a very kind referee (and I suspect it may have been
you because among other mistakes he pointed out that we
had spelled Carroll incorrectly in the reference) and
ultimately it was published as a Rapid Comm paper in PRD.
That was my first paper in the field of astro-particle
particle physics -the field wwhich has supplied my meal tickets ever since.
Reading your remarks about quintessence generating
polarization I thought of an idea (which you may have
already thought of and discarded). Generally you improve
the bounds on such couplings when you have a long-baseline
for the photon. Now the longest baseline that is available
for observation is that traversed by CMB photons from the
LSS to us. The baseline is of the order of the age of the
universe. If there is some quintessence type field
with pseudosclar coupling to photons then it will
contribute to the polarizations of the CMB (on which there
are good constraints from WMAP-3). So using the WMAP
polarization results one would probably get the best
bounds on these type of couplings…?
Best wishes,
Subhendra
Sean – There are definately many such models. My impression is that the new fields can generally be coupled only to gravity to avoid other very tight bounds. Our paper addressed specifically the so-called Einstein-Aether, or new Aether, theories but I am pretty sure that, unless finely tuned, any coupling to gravity would alter the dispersion relation of the graviton to give some subluminal mode that can be radiated in a Cerenkov process.
Jacobson and Foster take this to mean that, in their “ae-theory,” the parameters should be chosen such that the effective graviton modes are all super-luminal. We discounted this possibility from the start, but I understand that some people are not so conventional.
Is that more clear? I am not really up on the current trends in spontaneous Lorentz breaking; are there any more plausable theories that you know of? Is superluminal propagation a very good out? I know its impossible to rule out, but I feel it is rather unattractive theoretically. Thanks.
Pardon the stupid question, but isn’t there already a preferred timelike direction in spacetime, the one in which the universe is expanding and entropy is increasing?
Sorry, for a moment there you did look a bit like an astronomer. My mistake. 😛
Subhendra, thanks for writing. The CMB is certainly a promising place to look; but I doubt at this point that the limits are very good, just because the errors on the polarization angles are quite large. (And the *distance* to the CMB isn’t that much more than to a high-redshift galaxy, even if the redshift is much greater.) I don’t know if anyone has actually looked at the limits, but I know that people did anticipate the possibility:
http://arxiv.org/abs/astro-ph/9812088
Uninitiated, sure, the cosmological rest frame and the entropy gradient definitely do define a direction in spacetime, at least on average over large scales. But that’s due to the evolution of matter fields; I was imagining a vector that would exist even in vacuum.
Joshua, I haven’t been following the debates closely, although I have talked a bit with Jacobson about this. I also tend to worry about superluminal propagation, but someone needs to sit down and show what would actually go wrong. I think Eugene is working on this, actually.
I get it now. Thanks for clarifying, Sean! It’s one of your great talents.
Sean,
Thanks for the reference. I checked the citations of this paper to see if some-one actually has used the WMAP data for putting some bounds and found a recent paper ( astro-ph/0601095 – acccepted in PRL) in which they claim that there is a signal(!)for a non-zero external vector field which couples to photons, from the WMAP+Boomerang data.
Sean, if the results of
this are true, would that imply the existence of a vector field?
Shantanu, it would imply Lorentz violation of some sort, which may or may not take the form of a vector field. But more likely it’s just not right; it seems hard to make it consistent with other experimental bounds.
i’m just an ignorant bystander, but i’m going to open my big yap anyway:
if i understand this discussion at all, it may be the case that the universe has an inherent “handedness.”
what the cause may be is poorly understood (if at all), but this handedness exists, nonetheless.
is this the essence of the discussion?
The essence is that some people thought there was evidence for the universe having a handedness, but those people were not right. (To be careful: we’ve known for some time that some particle interactions, specifically the weak nuclear force, definitely exhibit a handedness — they violate parity. But there is no evidence that space itself has any such property.)
Sean says: “It was the only time in my life when I worked feverishly over the course of a couple of days to write a paper from scratch.”
Ah….that’s what happens when there is DATA!! Counting down desperately to the LHC….