Sir Michael Atiyah, one of the world’s greatest living mathematicians, has proposed a derivation of α, the fine-structure constant of quantum electrodynamics. A preprint is here. The math here is not my forte, but from the theoretical-physics point of view, this seems misguided to me.
(He’s also proposed a proof of the Riemann conjecture, I have zero insight to give there.)
Caveat: Michael Atiyah is a smart cookie and has accomplished way more than I ever will. It’s certainly possible that, despite the considerations I mention here, he’s somehow onto something, and if so I’ll join in the general celebration. But I honestly think what I’m saying here is on the right track.
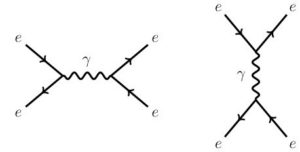
In quantum electrodynamics (QED), α tells us the strength of the electromagnetic interaction. Numerically it’s approximately 1/137. If it were larger, electromagnetism would be stronger, atoms would be smaller, etc; and inversely if it were smaller. It’s the number that tells us the overall strength of QED interactions between electrons and photons, as calculated by diagrams like these.
 As Atiyah notes, in some sense α is a fundamental dimensionless numerical quantity like e or π. As such it is tempting to try to “derive” its value from some deeper principles. Arthur Eddington famously tried to derive exactly 1/137, but failed; Atiyah cites him approvingly.
As Atiyah notes, in some sense α is a fundamental dimensionless numerical quantity like e or π. As such it is tempting to try to “derive” its value from some deeper principles. Arthur Eddington famously tried to derive exactly 1/137, but failed; Atiyah cites him approvingly.
But to a modern physicist, this seems like a misguided quest. First, because renormalization theory teaches us that α isn’t really a number at all; it’s a function. In particular, it’s a function of the total amount of momentum involved in the interaction you are considering. Essentially, the strength of electromagnetism is slightly different for processes happening at different energies. Atiyah isn’t even trying to derive a function, just a number.
This is basically the objection given by Sabine Hossenfelder. But to be as charitable as possible, I don’t think it’s absolutely a knock-down objection. There is a limit we can take as the momentum goes to zero, at which point α is a single number. Atiyah mentions nothing about this, which should give us skepticism that he’s on the right track, but it’s conceivable.
More importantly, I think, is the fact that α isn’t really fundamental at all. The Feynman diagrams we drew above are the simple ones, but to any given process there are also much more complicated ones, e.g.
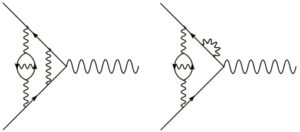 And in fact, the total answer we get depends not only on the properties of electrons and photons, but on all of the other particles that could appear as virtual particles in these complicated diagrams. So what you and I measure as the fine-structure constant actually depends on things like the mass of the top quark and the coupling of the Higgs boson. Again, nowhere to be found in Atiyah’s paper.
And in fact, the total answer we get depends not only on the properties of electrons and photons, but on all of the other particles that could appear as virtual particles in these complicated diagrams. So what you and I measure as the fine-structure constant actually depends on things like the mass of the top quark and the coupling of the Higgs boson. Again, nowhere to be found in Atiyah’s paper.
Most importantly, in my mind, is that not only is α not fundamental, QED itself is not fundamental. It’s possible that the strong, weak, and electromagnetic forces are combined into some Grand Unified theory, but we honestly don’t know at this point. However, we do know, thanks to Weinberg and Salam, that the weak and electromagnetic forces are unified into the electroweak theory. In QED, α is related to the “elementary electric charge” e by the simple formula α = e2/4π. (I’ve set annoying things like Planck’s constant and the speed of light equal to one. And note that this e has nothing to do with the base of natural logarithms, e = 2.71828.) So if you’re “deriving” α, you’re really deriving e.
But e is absolutely not fundamental. In the electroweak theory, we have two coupling constants, g and g’ (for “weak isospin” and “weak hypercharge,” if you must know). There is also a “weak mixing angle” or “Weinberg angle” θW relating how the original gauge bosons get projected onto the photon and W/Z bosons after spontaneous symmetry breaking. In terms of these, we have a formula for the elementary electric charge: e = g sinθW. The elementary electric charge isn’t one of the basic ingredients of nature; it’s just something we observe fairly directly at low energies, after a bunch of complicated stuff happens at higher energies.
Not a whit of this appears in Atiyah’s paper. Indeed, as far as I can tell, there’s nothing in there about electromagnetism or QED; it just seems to be a way to calculate a number that is close enough to the measured value of α that he could plausibly claim it’s exactly right. (Though skepticism has been raised by people trying to reproduce his numerical result.) I couldn’t see any physical motivation for the fine-structure constant to have this particular value
These are not arguments why Atiyah’s particular derivation is wrong; they’re arguments why no such derivation should ever be possible. α isn’t the kind of thing for which we should expect to be able to derive a fundamental formula, it’s a messy low-energy manifestation of a lot of complicated inputs. It would be like trying to derive a fundamental formula for the average temperature in Los Angeles.
Again, I could be wrong about this. It’s possible that, despite all the reasons why we should expect α to be a messy combination of many different inputs, some mathematically elegant formula is secretly behind it all. But knowing what we know now, I wouldn’t bet on it.
Must admit I started worrying when I saw a couple of references noted as “submitted” and “forthcoming”, including one on a supposed new proof of the Feit-Thompson theorem which apparently he circulated informally at a conference last year and was said to contain at least one mistake.
Seems to me it is a misguided attempt, most likely with an element of last-minute desperation (as he is nearly 80), to “tie up loose ends” and solve several problems that have obviously preoccupied and intrigued him for years, and whose solution he has long felt should be possible by applying the kind of maths with which he is familiar and in many famous cases pioneered!
But even if it can seem undignified with declining powers, it’s brave to fight to the last, and, who knows, with his distinguished record and doubtless vast erudition, maybe there’s some truth or useful insights in these latest papers, even if not quite what he claims.
Thank you, nice article.
So, anecdotically, old mathematicians are like the rumor on old physicists, looking for spikes in other areas to hit with their old hammers!? Not very surprising and not totally useless either (queue Schrödinger and DNA).
At least I had to refresh somewhat on weak functions to try to grok and grep out of the original paper.
Also from the pre-print; “Finally, this explanation of α should put an end to the anthropic principle, and the mystery of the fine-tuning of the constants of nature. Nobody has ever wondered what the Universe would be like if π were not equal to 3.14159265…”
I’m pretty sure people _have_ wondered what the universe would be like for different values of π. But beyond that, it’s all well above my level of understanding. I do have a very strong suspicion of ‘outsiders’ proposing solutions within another field. More often than not it’s embarrassingly naive.
Sean, your critique of Atiyah’s effort makes a number of clear observations about the nature of the fine-structure constant, especially with reference to elementary charge and the anomalies of magnetic moment (g-factor). As you suggest, context remains very important to the meaning of proportions. It has everything to do with the meaning and order of emergent properties within the context of processes. Universal processes will always remain fundamentally tied to laws of conservation. QED and QCD approach those limits of association through better understandings of symmetry and symmetry breaking. The question about what governs those limits is the key to universal topology and combinatorics. It also determines the differences between strict and interactive causality.
Atiyah is in good company. A famous paper by Beck, Bethe, and Riezler, recounted in “A Random Walk in Science” (1973), derived the fine structure constant thus:
“…According to Eddington, each electron has 1/α degrees of freedom…To obtain absolute zero temperature we therefore have to remove from the substance (2/α-1) degrees of freedom…For the absolute zero temperature we therefore obtain
T_0 = -(2/α – 1) degrees.
If we take T_0 = -273 we obtain for 1/α the value of 137, which agrees within limits with the number obtained by an entirely different method.”
The BBR paper was published in Die Naturwissenshaften in 1931, and while it might not have fully established the value of α, it did establish that the editors had a good sense of humor.
The below formula falls out a system that mimics QM/QFT . The system is very similar to Buffon’s needle (a generalized version) which is related to pi. However this system is derived from more basic relational geometric system.
https://en.wikipedia.org/wiki/Buffon%27s_needle
proton electron mass ratio =3*(9/2)*(1/alpha-1) -1/3= 1836.152655 using codata for alpha
if we use 1/alpha =137.036005 which is very close to average of codata and neutron Compton wave experiments base precision qed tests. Then
proton electron mass ratio =3*(9/2)*(1/alpha-1) -1/3= 1836.1526734
Of course the formula can be inverted to solve for alpha using proton/electron mass ratio. All this shows that the fundamental constants are related through a certain system and cannot be computed naively. Moreover, the full system also shows the running phase of alpha as interaction energies become much higher.
At first I thought that this Atiyah paper was a spoof, but apparently not. It has a certain charm on a second reading. The “Atiyah response” to Sean’s article above is “outlined” in page 2:
“I should point out that physicists already have a model for alpha which fits remarkably well with experimental data. This model rests on Feynman diagrams, but these have shaky foundations and involve herculean computational work.”
Of even greater interest has to be paragraph 9.4:
“The 4 division algebras, the reals R, the complex numbers C, the quaternions H and the octonions O translate into the 4 basic forces. The electro-weak from R and C, the strong force from H and gravity from O.”
Apparently all this will be explained in later papers, so I hope that Sean will be ready with a response (especially on Gravity and the octonions!)
Thank you, Sean, for calling bullshit on Atiyah’s claim.
This is refreshing intellectual honesty compared to the obsequious silence of the mathematics community regarding his supposed “proof” of the Riemann Hypothesis which seems to be “not even wrong” (This can be read between the lines on various sites and blogs but nobody is saying it outright).
As a result, a lot of non-specialists are coming away with the impression that this was the equivalent of Andrew Wiles’ proof of FLT, which will take months to unravel in detail. That certainly isn’t the case here.
The excuse being given is that the “diplomatic silence” is out of respect for Atiyah’s past achievements.
But I think it is quite possible to negate someone’s claim without being disrespectful – as your post shows.
Maybe mathematicians can take a lesson from your post and show some spine..
Is Sean saying that Feynman, Lederman and other physicists are misguided when they say the number 137 has some significance? Were their points made before we realized that the fine structure constant changed at higher energies?
I read Atiyah’s paper but I didn’t understand it, and didn’t see the TQFT I was looking for. However I noticed his chapter 10 heading, which was I would just like to understand the electron. And I would say this: when you do, you understand that the electron’s field is what it is. It isn’t a point particle, so renormalization is a fudge. Which means it doesn’t feel good to be using renormalization to calculate the fine structure constant. Not when α = e²/4π applies because it takes two to tango and 4π is a solid angle. By the by, c is not constant, which is why α is thought to vary with gravitational potential. Solar probe plus was going to measure this, but the experiment got dropped. Pity.
Just imagine he’s right. It would open a door to a lot of progress in quantum simulation. We should take this seriously…
If we had a more precise measurement of the fine structure constant, then we could compare Atiyah’s predicted number to the actual one.
How hard would it be to add more decimal points to our measurement of this constant?
Rephrasing Descartes ‘I criticize (the earlier the better), therefore I am”, some physicists have an inner drive to say something immediately, therefore they are. Given the history of false claims, Atiyah’s included, I understand why mathematicians are skeptical. But why got some physicists alerted to defend the holiness of the fine structure constant when (i) They have not seen the paper, and (ii) They clearly understand that that Atiyah’s RH paper is absolutely not about physics whatsoever. Atiyah should have called the special number he approached the ‘fine structure constant’, just putting it in apostrophes ,because its value happens to highly resembles the physical fine structure constant.
I mostly agree with you.
But your discussion in terms of Feynman diagrams gives a certain primacy to perturbation theory.
Is it not conceivable that the low-energy limit of \alpha is determined by some fundamental law we don’t yet know, and that the current theory of QED, and all the renormalization, is constrained to yield this fundamental value, in a way which is obscured by our perturbative approach to a theory which already has a lot of parameters in it that arose through symmetry breaking et cetera?
[NB Haven’t yet read the Atiyah paper, and of course – with Eddington firmly in mind – I’m also very skeptical.]
Following on from David Rutten’s comment about Atiyah’s statement: “Nobody has ever wondered what the Universe would be like if π were not equal to…” I note that Douglas Hofstadter’s Metamagical Themas, page 36 addresses precisely this point in an amusing graphical manner. Check out these scans:
https://twitter.com/propentropy/status/1044442799049830401
Several things really puzzled me about this paper. Then I read the Acknowledgements, that part of any paper that most of us (including funding bodies) routinely skip. FWIW, the following are my thoughts on what we are looking at.
Atiyah writes:
“..special thanks to Gerard ‘t Hooft who shared his critical insight with me in Singapore in January [2018?] and challenged me to explain alpha….”
Unless we were part of the conversation we don’t know what ‘t Hooft’s insight was. Nor do we know what Atiyah was discussing with him, although it might be reasonable to think that it had something to do with the Foundations of Physics paper cited as [8]. We know that ‘t Hooft challenged Atiyah to provide an explanation of alpha within that framework. Note, *not* as a function of energy.#
IMHO what we are looking at here is a sketch response to ‘t Hooft (possibly with a view to later publication in a more refined form). This would go some way towards explaining the gaps; the use of the first person; and various other points that have been raised here and elsewhere. The leaps in the argument are probably in part due to our lack of understanding of the context and in part because Atiyah will draw on insights garnered over many years not necessary to be fleshed out in a sketch argument.
How such a draft might have found its way into the wider world one can only guess at.
Aephraim– I basically agree with this. The current way of looking at things is that there are a number of “fundamental” inputs that go though a complicated process of renormalization and symmetry breaking (including SU(2)xU(1) breaking) to give the low-energy fine-structure constant, and therefore we shouldn’t expect any simple formula for the latter. But it’s conceivable that this understanding is simply backwards. I see no evidence or argumentation for such a radical upending of our current understanding in Atiyah’s paper, so I remain skeptical.
I see problems with both a strictly mathematicians’ approach AND a strictly particle physicists’ approach. Yes Atiyah’s FSC paper is vague (not detailed enough in places) both in many respects both mathematically and physically. However, everybody is vague in their expositions, because of nature of modeling ideas. With one side saying: “I don’t understand the mathematics” and the other side saying “I don’t understand the physics” — we have a problem here. It is a good discussion to have, but watch out for saying “I don’t understand it, therefore it is not applicable”.
Sean says: “Renormalization teaches us …”. To me raises a red flag to me. Renormalization is a mathematical trick — to say that “things are too complicated” (therefore we will chose a narrow band (a gauge) ) and treat it as 2D Euclidean “thin enough” approximation and ASSUME that the “real number” constants (mixing angles or scale factors) gives you precise process information in higher measure spaces (e.g., 3D, Orthogonal, Simplicial, Lie Groups) reminds me of Nima’s very informative lectures but EQUALLY VAGUE (and hand waving via tensors (assuming “real numbers” and Hemitian products as a foundation)) rant on the “problems with” coming up with a theory of quantum gravity.
This is good that the mathematicians and the physicists enjoy dismissing each other, so that comparative science and relational complexity has a wide open lattice to play with. It’s a Dedekind’s unreal unkind cut.
You write, ” However, we do know, thanks to Weinberg and Salam, that the weak and electromagnetic forces are unified into the electroweak theory. …”
Wasn’t Sheldon Glashow, the first to notice that these two forces are one at higher energies?
Here in Munich there is an attempt to calculate the fine structure constant that does takes care of the nuclear interactions and of the running with energy: http://www.motionmountain.net/research.html
Schiller’s approach first explains/predicts the particle spectrum and the four forces, and only afterwards attempts to calculate alpha. That sequence sounds much more trustworthy to me.
Sorry if this is a stupid question, but what exactly do you mean by ‘fundamental’ in this context? I assume you mean that it cannot be broken into smaller parts , i.e., is minimal. But if there is a grand unification, then nothing is really fundamental (except the amorphous unified state itself). Or do you mean that it must have a constant value? Perhaps we could define something as being fundamental if its preferred, low-energy state (i.e., its settled state) is necessary for the universe to be the way it is, and never mind how it got there (?)
I enjoyed reading this for the light it cast on particle physics – I hadn’t known of the connection between the weak coupling constants and e. I was under the impression that it was a fundamental constant! I too am sceptical of the claims made in Atiyahs paper though of course I acknowledge his immense contributions to building bridges between mathematics and physics.
17 lines about primes, and only 5 – about the Riemann hypothesis:
1) Any composite number is a product of k primes, k=2, 3, 4, … All composite numbers can be represented as an infinite set of Cs of infinite subsets of Csk (each Csk includes only those numbers that have k multipliers). All numbers in each particular Csk are the values of the arithmetic function Fcsk “product of k numbers” or, what is the same, Fcsk is a function of k arguments.
2) It is important to note once again the following nuance: any Fcsk is not a function of k VALUES of the same INDEPENDENT VARIABLE, but is a function of k different INDEPENDENT VARIABLES (primes in the abovementioned product [computationally] are not connected with each other; the presence of all possible combinations of such numbers in any Fcsk only confirms this fact). It does not matter the presence of an exotic situation (each of these independent variables is given on the minimum possible interval and therefore consists of only one number).
3) Functions with DIFFERENT quantity of independent variables is DIFFERENT functions. They do not depend on each other and cannot be expressed through each other to get some single, compact, with convenient quantity of arguments, function.
4) Consequently, the Fcs regularity, which determines ALL composite numbers, is a piecewise function consisting of an infinite set of INDEPENDENT functions of Fcsk. It is clear that the complexity of the Fcs function can only be infinite.
5) The position of specific primes among the natural numbers is uniquely determined by the position of the neighboring composite numbers. This means that the regularity Fpr, which governs all primes, depends entirely on the regularity of the Fcs, which determines all composite numbers.
6) It does not require proof that if the argument (in our case: Fcs) of a function (in our case: Fpr) has infinite complexity, then any such function will also have infinite complexity (a similar, but even more hopeless situation occurs in the goal functions of the problems from the notorious class NP: that is why PNP). Therefore, the Fpr regularity can only have infinite complexity.
7) Compact and elegant regularity, which is presented in the Riemann hypothesis, the Riemann zeta-function, which perfectly tracks a huge number of known primes, does not satisfy this condition. The zeta-function is inextricably linked to Fpr: knowing the quantity of primes in an arbitrary finite interval in one way or another implies knowing the fact of existence of each such numbers in this interval. Moreover the second is possible and self-sufficient without the first, and the first, to avoid undetected primes, requires at least mandatory verification by the second. Will have to assume that the proverbial state of affairs mentioned in “3)” is not fulfilled in nature only for Fpr and for Riemann zeta-function – or Riemann zeta-function reveals not all primes.
***
The paper «On a regularity that determines prime numbers» about this uncomfortable feature of primes was published exactly 3 years ago.
In the paper was also said about the extremely low probability to find a reliable function, if we know only some values of this function. In this case, we were talking about an infinite set of primes as the values of the some function Fpr that actually governs them: the vast majority of primes we do not know today and will never know.
Also was said about the principal impossibility of reliably PROVING the complete identity of the algebraic properties of any function-candidate for the role of Fpr with the desired physical reality, if we do not know from OTHER sources the values of ALL those entities (in our case: all primes), for which this candidate claims full control. Even if this claim is absolutely true. Here: “algebraic properties” is the virtual landscape of the zeta-function, “physical reality” is the actual position of primes on the natural axis and their quantity at one or the other intervals.
You do treat him with respect, but does this need public attention? This was just sad. You don’t need to be an expert to be able to judge the paper and then to understand the implication of this.
So Atiyah would be following Eddington, becoming a crackpot with age
But what about this Salingaros study ?
https://patterns.architexturez.net/system/files/Some_remarks_on_the_algebra_of_Eddington.pdf
Moreover, Eddington has predicted the Tau, he called ‘Heavy Mesotron’, with a correct estimation of mass, 35 years before its surprising discovery.
It seems that comething got wrong in the Sean arguments against the fundamental character of electric charge. This is typical of an excess of reductionist thinking. Invoquing a theory with other parameters g and g’ is not a logical reason to think a = 137.036 has no mathematical representation.
I’m skeptical, but things like pi and 1/2 show up all over the place in physics, and often their presence provides geometric insight into the physics of the situation. For example, if I see 4*pi in a term somewhere, I would suspect that some aspect of the physics involves spherical boundaries or spatial curvature.
Perhaps Atiyah has done something with the mathematics of Feynman diagrams and shown that the series allow some convergence on alpha, much as the sum of the harmonic series allows a convergence on gamma. If this is the case, then there may be some analytic or geometric reason that the mathematical process describes some aspect of the physics of the fine structure constant.
Feynman diagrams involve a convergent geometric summation, so it is possible that the same mathematics is involved as is involved in the Riemann hypothesis. Mathematics is deep this way. There is both more and less than one expects and a surprising number of different things turn out to be aspects of the same thing.